们研究了使用恒定增益带宽积(恒定英镑)
运算放大器的局限性,我们发现工作频率范围是在运算
放大器的极点频率f b和积分器的单位增益频率f 0。这是环路增益T 化的范围,因此也是实际传递函数 H 与理想H理想值的偏差化的范围。
我们现在希望更详细地研究这种偏差。在继续之前,我们回顾一下有关积分器限制的第二篇文章,H还受到运算放大器的输出阻抗z o的影响,因为 z o允许信号在运算放大器周围馈通。
下面,我们假设 |z o | 远小于积分器的电阻R,因此可以忽略馈通。在这些条件下,我们重复使用之前文章中的发现,并针对图 1(a) 的电路编写:H(jf)=VoVi=H理想(jf)11+1/T(jf)(1)
在哪里
H理想(jf)=?1jf/fo(2)
fo=12πRC(3)
此外,环路增益| T | 可视化为开环增益 | 之间的差异。一个| 和噪声增益 |1/ β | (见图 1(b),顶部),其中
1β=H理想+1(4)
图 1. (a) 积分器和 (b) 幅度 |H| 的线性化图 (上)和Ph[H]相(下)。
幅度误差
使用方程(1)和(2),我们写出
\[\左 | H \右| = \左 | H_{理想} \right | \次\左 | \frac {1}{1+1/T} \right | = \frac {1}{f/f_o} \times \frac {1}{\left |1+1/T \right |} = \frac {1}{f/(f_o/\left | 1+1/ T \右 |)}\]
表明在幅度方面,电路仍然充当积分器,但单位增益频率为
\[f_o ' = \frac {f_o}{\left | 1+1/T \right |} \: \: \: \: \: \: \: \: \: \: (5)\]
参考图 1(b),顶部,我们估计 | T(jf 0 ) | 利用英镑的稳定性: | T(jf 0 ) |×f 0 = 1× ft,这给出 | T(jf 0 )| = f t / f 0。代入方程(5)可得
f′o?fo1+fo/ft(6)
单位增益频率的下移提供了一种方便的方法来可视化 | 的偏离。哈| 来自| H理想|。这种偏离称为幅度误差。
相位误差
根据公式(2),理想情况下积分器的相位角为 Ph[ H Ideal ] = Ph[–1] – Ph[ j ] = 180 – 90 = 90°。然而,由于积分器的极对,Ph[ H ] 在其有用频率范围的低端和高端都将偏离 90°(见图 1b ,底部)。
我们将在下一篇文章中看到, f 0附近的相位误差在基于积分器的
滤波器(例如状态变量滤波器和双二阶滤波器类型)中特别值得关注。该误差为 ? phi = –tan -1 ( f/f t )。精心设计的积分器具有 f 0 << f t ,因此在 f 0附近我们近似为
????f/ft(7)
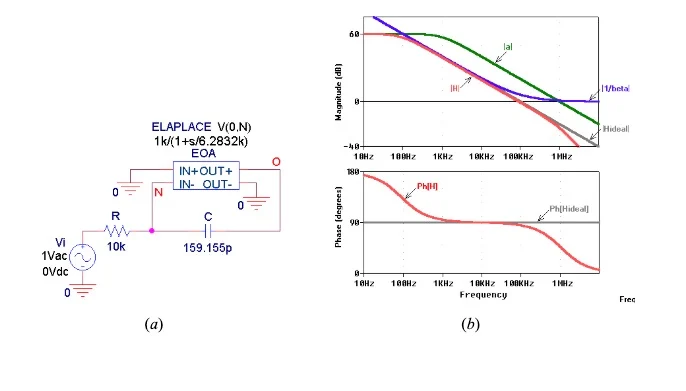
图 2. (a) f 0 = 100 kHz 且 f t = 1 MHz 的 PSpice 积分器。(b) 幅度图和相位图。
作为一个实际示例,请考虑图 2(a) 中的 PSpice 积分器,它使用拉普拉斯模块来模拟 GBP = 1 MHz 的运算放大器。根据等式(3),f 0 = 100 kHz。
方程 (6) 和 (7) 提供了估计值
f 0 = 100 kHz
-5.71°,与 90.53 kHz 的测量值相当一致,并且 – 4.64°。
我们观察到,幅度误差不一定是坏事,因为我们总是可以通过适当预失真RC产品的值来补偿它。例如,将图 1 中的 C 从 159.155 pF 降低到 142.473 pF,同时保持R不变,将提高 f 0所需的量,以确保
kHz。
或者,我们可以保持C不变,并将R从 10.0 kΩ 降低至 8.952 kΩ。
