如果您读过上一篇文章,您就会知道我们可以使用 t 分布而不是正态分布来对原假设进行建模,以评估统计显着性。当我们使用较小的样本量时,t 分布是有利的,因为在这种情况下它会产生更准确的置信区间。
t 分布的形状根据参数 \(\nu\) 变化,参数 \(\nu\) 表示自由度,由样本大小(用 n 表示)决定:
\[\nu=n-1\]
对于小样本量,t 分布的尾部比正态分布更重,表明观察到远离均值的值的概率更高。对于较大的样本量,t 分布和正态分布之间的差异越来越可以忽略不计。
这些特征在下面的图中很明显。
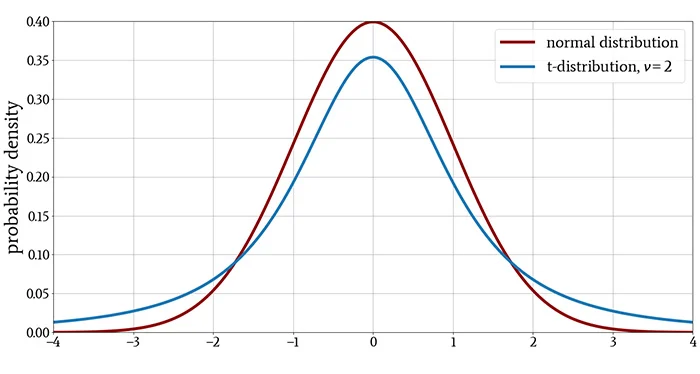
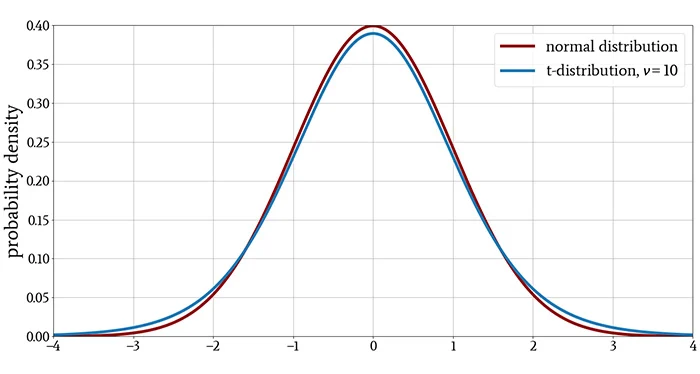
什么是 t 检验?
当我们执行 t 检验时,我们使用 t 分布对原假设进行建模。t 检验是一种通过比较实验期间观察到的因变量分布的平均值来评估统计显着性的方法。
t 检验要求自变量是双变量,即只有两个可能的值。例如,如果实验中的自变量是温度,如果我们需要分析仅与两个温度相关的数据,则可以使用 t 检验。如果我们在三个或更多温度下收集数据,我们将需要使用一种不同的统计检验,称为单向方差分析 (ANOVA)。
您可能还记得之前的文章,统计检验有参数和非参数两种形式,并且仅当数据集表现出足够的正态性时才使用参数检验。t 检验是一种参数检验。因此,在应用 t 检验之前,我们必须确保因变量的测量值呈正态分布。
此外,实验期间产生的因变量分布必须表现出一致的方差。换句话说,如果自变量的变化使分布向左或向右移动(这相当于改变均值),我们可以应用 t 检验,但如果它改变了分布的形状(这相当于改变方差)。
t 值
执行 t 检验时,我们通过计算 t 值(也称为 t 统计量)来比较样本均值:
\[t=\frac{\bar{x}-\mu}{s/\sqrt{n}}\]
其中\[\bar{x}\]是样本均值(即因变量测量值的均值),\[\mu\]是总体均值,s是样本的标准差,n是样本大小。
在许多实验中,我们无法确切地知道总体平均值,并且必须接受基于任何可用数据的估计值。在这种情况下,\[\mu\] 可以更准确地识别为建议的总体平均值。
此外,“总体平均值”可能只是我们想要与通过实验获得的观察结果进行比较的其他值。例如,我们可能有大量数据表明系统在某一温度(可能是室温)下的性能。
与室温性能相对应的值成为总体平均值,样本平均值是通过记录系统在例如 70°C 的温度室中运行时的有限数量的性能数据来生成的。
有不同类型的 t 检验适合不同的实验条件。在本文中,我们将使用单样本 t 检验,其执行方式如下:
选择显着性水平。
找到与所选显着性水平和自由度相对应的临界值(回想一下 \(\nu\) = n – 1)。常见显着性水平的临界值可以很容易地从表格中获得,例如这张表;请注意,“自由度”通常缩写为“df”(或“DF”)。
如上所示计算 t 值,其中 \[\mu\] 是用作比较点的现有值。
将 t 值与临界值进行比较。如果 t 值的大小大于临界值,我们拒绝原假设。
了解 t 检验和临界值
显着性水平(例如)0.05 表示,为了拒绝原假设,t 值必须位于仅包含概率质量 5% 的 t 分布部分。在下图中,红色阴影部分包含 5% 的概率质量,黑色垂直线表示临界值。
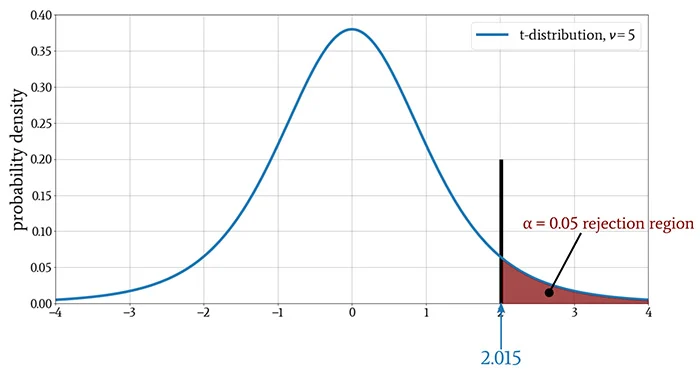
t 检验的思考过程是这样的:
我们假设原假设为真,即实验的自变量和因变量之间不存在关系。
我们通过计算 t 值将样本平均值与总体平均值进行比较。
我们解释相对于临界值的 t 值,这取决于样本大小和预定的显着性阈值。
如果 t 值的大小大于临界值(即,如果它位于拒绝区域中),则样本平均值与总体平均值相差甚远,以至于差异可能无法归因于偶然。因此,我们拒绝零假设,这相当于断言实验已经证明了自变量和因变量之间的关系。
一尾和二尾测试
上图对应于单尾 t 检验,这意味着拒绝区域仅在一个方向上延伸。如果我们只对因变量增加的关系的可能性感兴趣,我们会使用单尾检验。如果我们只对因变量减少的关系的可能性感兴趣,我们也会使用单尾检验。
另一方面,我们可能对相对于总体平均值的增加和减少感兴趣。为此,我们需要一个双尾检验,将拒绝区域分为均值以上的部分和均值以下的部分。
如果我们将单尾检验更改为双尾检验,我们会将相同的概率质量分为两部分,因此,双尾检验中的临界值将不同于单尾检验中的临界值测试。
下图是上图中所示 t 检验条件的双尾版本。

结论
我们讨论了如何计算 t 值以及如何执行单样本 t 检验,还介绍了单尾检验和双尾检验之间的区别。我们将在下一篇文章中通过将 t 检验知识应用到示例实验中来继续这个主题。



