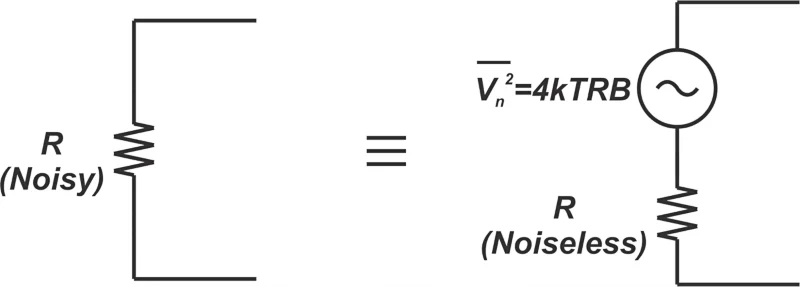在射频应用中,我们通常处理非常微弱的信号,这些信号很容易被电路内产生的噪声所掩盖。噪声水平终决定了
接收器能够可靠检测到的信号。因此,射频元件和系统的噪声特性至关重要。在我们关于噪声系数的介绍性文章中,我们了解了如何使用该指标来表征射频组件的噪声性能。
现在我们已经熟悉了基本概念,我们可以仔细研究噪声系数的定义,并讨论一些有时没有足够强调的微妙之处。这应该可以帮助您避免对该规范的错误解释。
噪声系数定义和噪声系数方程
电路的噪声因数 (F) 可定义为:
\[F=\frac{N_o}{GN_i}\]
等式 1。
在哪里:
No 是输出端的总噪声,包括电路内部噪声源的影响和源阻抗的噪声
Ni是源阻抗在电路输入端产生的 噪声
G是级的功率增益
虽然这个解释是正确的,实际上在一些参考文献中也提供了类似的解释,例如广泛使用的 教科书“模拟
集成电路的分析与设计”的第四版,作者是Paul R. Gray,但它并没有提供所有细节噪声系数定义。根据IEEE 定义,N i 是温度 T 0 = 290 K°(或 16.85 °C)时源
电阻器的可用热噪声功率。这个温度比舒适的室温要冷一点;然而,在射频工作中有时也将其称为室温。
此外,IEEE定义指出,No是 器件输出处的??可用噪声功率,G是器件的可用功率增益。这里的关键点是规范的参考温度 T 0 = 290 K°,以及用于描述方程 Ni 、No 和 G 的所有三个参数的描述符“可用”。在本文的其余部分中,我们将详细讨论“T 0 = 290 K 时的可用噪声功率”的含义。
可用噪声功率
热激发电荷载流子的随机运动表现为电阻器中的噪声。可以通过添加与无噪声电阻器串联的噪声电压源来对噪声电阻器进行建模,如下图 1 所示。
噪声电阻器以及添加与无噪声电阻器串联的噪声电压源的示例图。
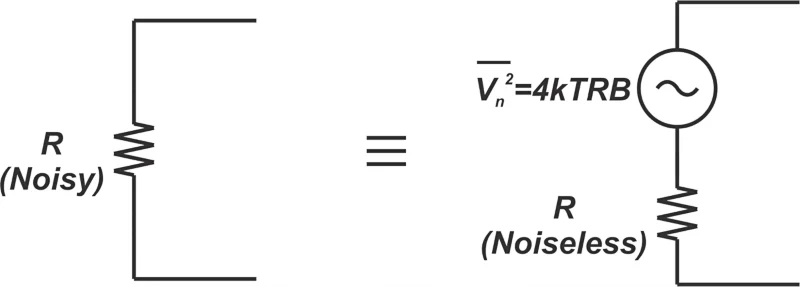
图 1. 噪声电阻器以及添加与无噪声电阻器串联的噪声电压源的示例图。
噪声电压源的PSD(功率谱密度)为 \( \overline {V_n^2} = 4 \space kTRB\),其中:
k 是玻尔兹曼常数 (1.38 × 10 -23 焦耳/开尔文)
T 是开尔文温度
B 是考虑的带宽(赫兹)
在噪声系数定义中,Ni是 源电阻器的可用噪声功率。现在的问题是,图1(b)中的电路可以提供的噪声功率是多少?从基本电路理论中,我们知道当
负载电阻等于源电阻时,传输的功率。因此,可以使用以下电路(图 2)来查找源电阻 R S的可用噪声功率。
用于查找源电阻器的可用噪声功率的电路图。

图 2. 用于查找源电阻器的可用噪声功率的电路图。
请记住,我们 在上图中使用了噪声源的RMS(均方根)值。由于一半的噪声电压出现在负载上,因此传递到匹配负载的噪声功率 R L = R S可以通过以下公式找到:
\[\begin{eqnarray}
P_{L} = \frac{V_{L}^2}{R_L} &=& \Big ( {\frac{V_{n,rms}}{2}} \Big ) ^ 2 \times \frac{1}{R_L} \\
&=& \frac{4kTR_SB}{4} \times \frac{1}{R_S} \\
&=& kTB
\end{eqnarray}\]
等式2。
这是噪声系数计算的重要结果。请注意,可用噪声功率与电阻值无关。无论是1mΩ电阻还是1MΩ电阻,可用的噪声功率都是kTB。在 1 Hz 带宽中,可用噪声功率为 kT。噪声系数定义基于 T 0 = 290 K 时的可用噪声功率 。以 dB 为单位表示 kT 0时,该参考温度下的可用噪声功率为 -174 dBm/Hz,计算如下:
\[10 log \big ( kT_0 \big )=10 log \big ( 1.38 \times 10^{-23} \times 290 \big ) \approx -174 \text{ } dBm\]
噪声系数指定添加噪声的相对量
由于噪声系数定义基于 Ni = kT 0 B,因此它指定了相对于 Ni 被添加到信号中的噪声的相对量。考虑我们在上一篇文章中推导出的以下噪声系数方程:
\[F=1+\frac{N_{o(添加)}}{N_{o(源)}}\]
这里,N o(source) 是源于源阻抗的输出噪声的一部分;N o(添加) 是电路本身产生的输出噪声的一部分,不包括源电阻的贡献。注意到 N o(source) = kT 0 BG,我们得到方程 3:
\[F=1+\frac{N_{o(添加)}}{kT_0BG}\]
等式 3。
为了更好地可视化上述方程的噪声项,请考虑图 3 中的下图,该图有时称为“噪声线”。
显示噪声线的图。
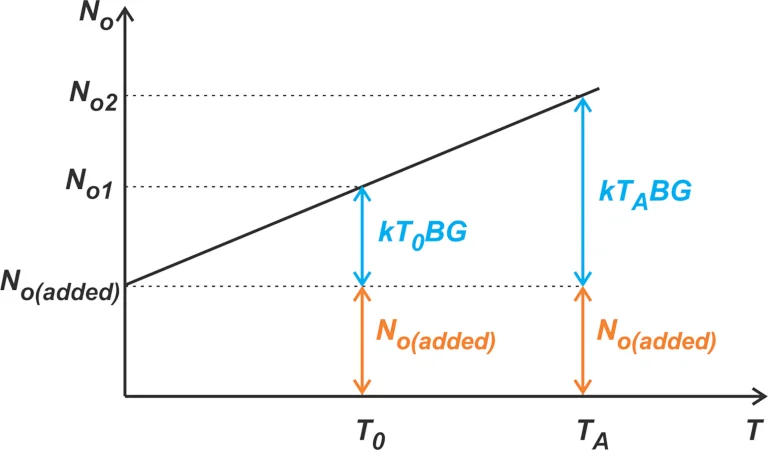
图 3. 显示噪声线的图。
在上图中,总输出噪声 No 相对于源电阻温度 T 绘制。如果 R S 无噪声(或 T = 0 K),则输出处出现的噪声将是被测设备或否(已添加)。当我们提高 R S的温度时,它的噪声贡献就会增加。噪声系数指标对应于 T = T 0 ,实际上指定了 T 0时 R S贡献的输出噪声(即 kT 0 BG)与被测器件的输出噪声之比 (No (added) )。例如,如果系统的噪声系数为 F = 2(或 NF = 3 dB),我们知道 N o(added) 等于kT 0 BG。
从图中可以清楚地看出,R S 噪声与 No (添加)的比率 不是恒定的,而是随 T 变化。因此,如果 R S 处于 T 0以外的温度,我们不能直接使用噪声系数方程来计算求输出噪声。 相反,我们应该首先找到来自 DUT(被测设备)的噪声,添加感兴趣温度下 R S的噪声,计算总输出噪声。
我们还可以通过将分数的分子和分母除以级的功率增益,用输入参考噪声值来表达方程 3。由此得出公式 4:
\[F=1+\frac{N_{i(添加)}}{N_{i}}\]
等式 4。
在此等式中,Ni (添加) 是 DUT 贡献的输入参考噪声,Ni是 290 K 时源的可用噪声功率。同样,如果 F = 2,则由 DUT 贡献的输入参考噪声DUT 等于 Ni = kT 0 B。让我们看一个示例来阐明这些概念。
示例:使用噪声系数方程
放大器的噪声系数、带宽和增益分别为:
噪声系数 = 2.55 分贝
B = 10兆赫
增益 = 5.97 分贝
假设可用输入噪声为 kT A B,求两种不同情况下的输出噪声:1 - T A = 290 K 和 2 - T A = 150 K。
我们首先找到噪声系数和增益的线性值:
\[F=10^{\frac{NF}{10}}=10^{0.255}=1.8\]
\[G=10^{\frac{增益}{10}}=10^{0.597}=3.95\]
由于噪声系数的定义假设输入噪声是 T = 290 K 时的可用噪声功率,因此我们可以直接从公式 1 找到该温度下的输出噪声:
\[N_{o}=N_{i}FG=kT_{0}B\times FG\]
用分贝表示右侧,我们有:
\[\begin{eqnarray}
N_o &=& 10 log(kT_0) + 10log(BFG) \\
&=& -174 \text{ }dBm/Hz + 10 log(10 \times 10^{6} \times 1.8 \times 3.95) \\
&=& -95.48 \text{ } dBm
\end{eqnarray}\]
对于 T A = 150 K,我们不能直接使用噪声系数方程。然而,噪声系数方程可用于计算系统贡献的噪声。将 Ni = kT 0 B 代入 公式4,系统贡献的输入参考噪声为:
\[N_{i(添加)}=(F-1)kT_0B\]
当 F = 1.8 时,我们得到 Ni (added) = 0.8kT 0 B。因此,输入端的总噪声为:
\[N_{i(总计)}=N_{i(添加)}+kT_{A}B\\ =0.8kT_{0}B+kT_{A}B\]
将该值乘以系统增益 G,即可得出总输出噪声功率。在下面的等式中,我将 T A写成 T 0 以简化计算:
\[\begin{eqnarray}
N_{o(总计)}&=&G \big ( 0.8kT_0B+kT_A \frac{T_0}{T_0}B \big ) \\ &=& GkT_0B(
0.8 + \frac{150} {290})
\end{eqnarray}\]
用分贝表示右侧,我们有:
\[\begin{eqnarray}
N_{o(总计)} &=& 10 log(kT_0) + 10log(BG \times 1.317) \\ &=
& -174 \text{ }dBm/Hz + 10 log(10 \乘以 10^{6} \乘以 3.95 \乘以 1.317) \\
&=& -96.84 \text{ } dBm
\end{eqnarray}\]
如果不注意噪声系数的定义,可能会将 Ni = k × 150 × B 代入公式 1,这会产生No = -98.34 dBm 的错误结果。
物理温度或噪声温度
在上面的讨论中,我们强调了源电阻 R S的物理温度对我们 NF 计算的影响。通常,驱动点阻抗 (R S ) 与 DUT 处于相同的物理温度;然而,电路接收的输入噪声功率高于 kT 0 B。这种情况通常发生在级联系统中,其中信号链中的每个模块都会增加本底噪声。因此,级联中下游级的输入噪声通常超过 kT 0 B。在这些情况下,我们同样无法通过直接应用噪声系数方程找到输出噪声水平。相反,我们可以首先使用 NF 方程来找到电路产生的噪声 (N i(added)),然后使用该信息以及输入噪声级别来查找总输出噪声。 此外,定义输入噪声的等效噪声温度Te也很有帮助。这是可用热噪声功率 (kT e B) 等于输入噪声功率时的温度。若输入噪声功率为N 1,则其等效噪声温度为:
\[T_{e}=\frac{N_1}{kB}\]
噪声系数和等效噪声温度是元件噪声特性的可互换表征。在下一篇文章中,我们将介绍使用噪声温度概念的示例。
噪声系数指定 SNR 退化
噪声系数是电路引起的SNR(信噪比)下降的直接测量。这个说法是正确的;然而,它值得更多的解释。让我们再考虑一下上面讨论的例子。我们假设系统的噪声系数和增益分别为 NF = 2.55 dB 和增益 = 5.97 dB,并假设输入信号功率为 -40 dBm。当 R S 为 T A = 290 K 时,输入噪声功率为:
\[\begin{eqnarray}
N_i &=& 10 log(kT_0) + 10log(B) \\
&=& -174 \text{ }dBm/Hz + 10 log(10 \times 10^{6}) \\
&=& -104 \text{ } dBm
\end{eqnarray}\]
从示例的结果中,我们知道输出噪声功率为-95.48 dBm。图 4 总结了本示例输入和输出处的信号和噪声功率。
我们之前的示例的输入和输出处的信号和噪声功率的总结。

图 4. 前面示例的输入和输出处的信号和噪声功率汇总。
将输入信号乘以放大器的功率增益即可得出输出信号功率。图 4 还提供了输入和输出 SNR,以及 SNR 退化。请注意,比率 SNR i / SNR o 等于噪声系数 NF = 2.55 dB,这并不奇怪,因为我们知道该比率实际上是噪声系数的定义。然而, TA = 150 K的情况又如何呢?在这种情况下,输入噪声为 Ni = -106.86 dBm。图 5 总结了上一个示例的结果。
对上述示例的结果的另一个总结。
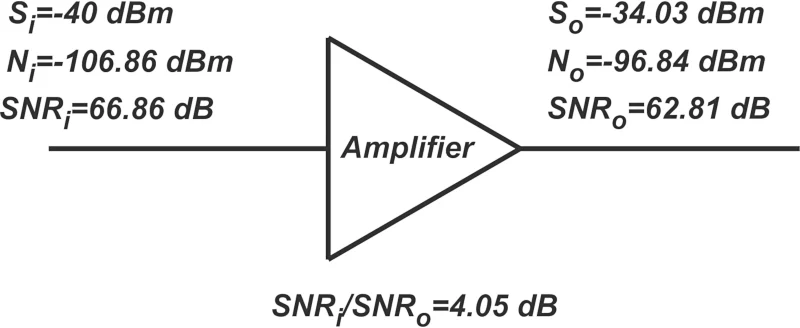
图 5. 上述示例结果的另一个总结。
正如您所看到的,SNR 下降 (SNR i / SNR o ) 现在大于 NF。这是因为输入噪声小于标准值,使得放大器的噪声贡献更加显着。因此,当输入噪声为 kT 0 B时,噪声系数决定了 SNR 的劣化。例如,如果电路的噪声系数为 7 dB,模块的输入噪声功率为 kT o B,则输出端的 SNR该块的 SNR 比输入 SNR 小 7 dB。