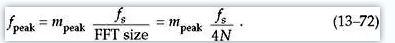在离散频谱分析的实际世界中,我们经常想要估计正弦曲线的频率(或感兴趣的非常窄带信号的中心频率)。
应用基 2 快速傅里叶变换 (FFT) 后,我们感兴趣的窄带信号很少恰好位于频率已知的 FFT 双中心上。因此,由于 FFT 的泄漏特性,具有 N 个时域样本的正弦曲线的离散频谱可能看起来像下面图 13-37(a) 中所示的幅度样本。
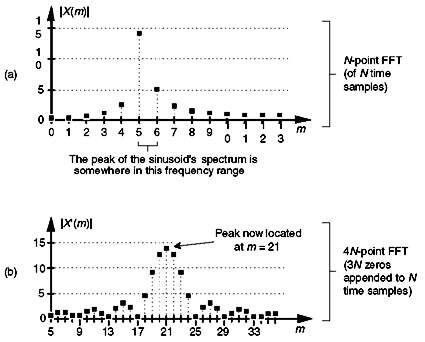
图13-37。频谱幅度:(a) N 点 FFT;(b) 4N 点 FFT。
在那里,我们看到正弦曲线的频谱峰值位于 FFT'sm = 5 和 m = 6 bin 中心之间。(变量 m 是 N 点 FFT 的频域索引。
FFT bin 间距为 f s /N,其中,一如既往,fs 是采样率。)仔细检查图 13-37(a),我们可以说正弦曲线位于 m = 5 和 m = 5.5 的范围内,因为我们可以看出,光谱样本比 m = 5 bin 中心更接近 m = 6 bin 中心。
在此示例中,实值正弦时间信号的频率为 5.25f s /N Hz。在这种情况下,我们的频率估计
分辨率是 FFT bin 间距的一半。
我们经常需要更好的频率估计分辨率,并且确实有多种方法可以提高该分辨率。
例如,我们可以收集 4N 个时域信号样本并执行 4N 点 FFT,从而将 bin 间距缩小为 f s /4N。或者我们可以用 3N 个零值样本填充(附加到原始时间样本的末尾)原始 N 个时间样本,并对延长的时间序列执行 4N 点 FFT。
这还将提供 f s /4N 的改进频率分辨率,如图 13-37(b) 所示。由于频谱峰值位于 binmpeak = 21,我们使用以下公式估计信号的中心频率(以 Hz 为单位):
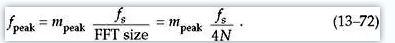
这两种方案都收集更多数据和补零,计算成本很高。科学文献中已经描述了许多其他提高精度频率测量的技术——从邻近的地球物理学领域到崇高的天体物理学研究——但这些方案中的大多数都追求精度,而不考虑计算的简单性。
在这里,我们描述了一种计算简单的频率估计方案。假设我们有实值窄带时间信号的 FFT 频谱样本 X(m),其幅度如下图13-38 所示。
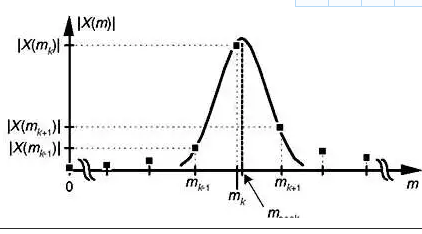
图13-38。窄带信号的 FFT 频谱幅度。