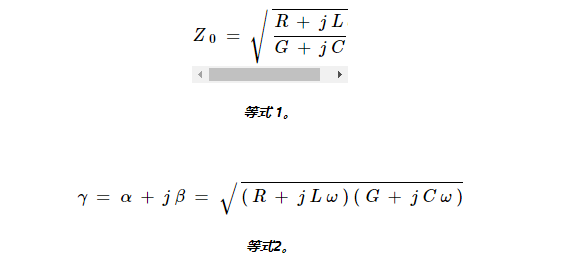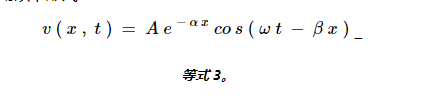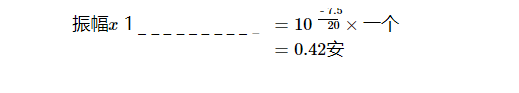许多应用中,无损可能是一个合理的假设,因为在高频下,
电感器的电抗通常远大于串联电阻 R,而
电容器的电抗通常远小于
分流电阻。尽管如此,仍有许多应用需要考虑传输线的损耗。
例如,可能需要在笔记本电脑或台式电脑等大型系统中沿着 12 英寸路径发送 USB 信号。这条长路径可能会导致大量丢失,从而严重扭曲数据并导致系统故障。了解有损传输线对于高速数字板和射频应用的设计非常有价值。
在本系列的接下来的几篇文章中,我们将了解传输线中的主要损耗机制,但在深入探讨之前,本文旨在定性描绘有损线的行为以及正弦曲线和方波的表现波信号沿着有损线路传播时会发生变化。
有损线方程
我们可以按照与无损线路类似的过程推导电压和电流方程 。对于有损线路,复数特征阻抗 Z 0 和复数传播常数 γ 如下面的等式 1 和 2 所示:
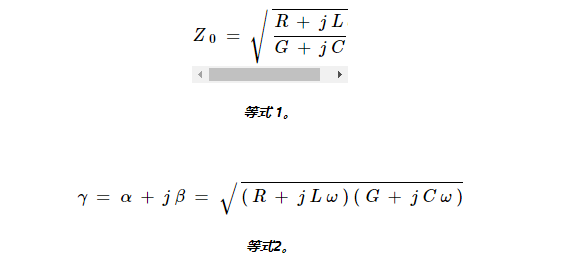
γ 的实部称为衰减常数 ?(单位为奈培每米);虚部称为传播常数 β(以弧度/米为单位)。如果该线沿 x 轴,则向前传播的电压波可采用以下形式:
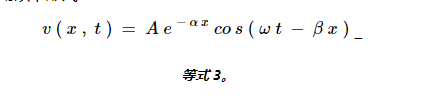
等式 3。
其中 A 是一个常数,可以从线路输入和输出端口的边界条件中找到。有损和无损情况之间的一个主要区别是指数项 e -x,它表明信号沿有损线路传播时会衰减。为了了解衰减对信号的影响,让我们看一些典型的波形。
比较无损和有损线路:正弦输入
考虑通过 40 英寸长的传输线将源阻抗为 R s的正弦输入 V s cos(?t)应用 到负载阻抗 R L (图 2(a))。假设没有反射波,前向波由公式 3 给出。
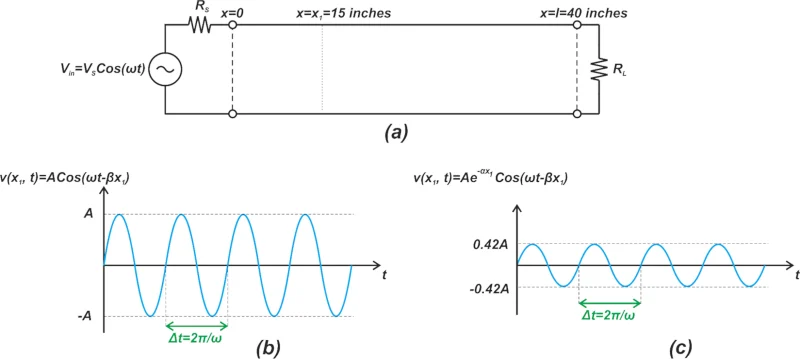
通过有损传输线的正弦信号传播
图 2. 通过有损传输线的正弦信号传播
在沿线的固定位置 x=x 1处,方程 3 中的 βx 项是恒定相位项,电压方程只是时间的正弦函数。对于无损线 (?=0),无论 x 的值如何,该正弦函数的幅度都是恒定的且等于 A。因此,在任意位置x处,波形的幅度为A,如图2(b)所示。
然而,对于非零值 ?,信号的幅度沿线减小。例如,如果线路损耗为每英寸 0.5 dB,则距离 x 1 =15 英寸处的总衰减为 7.5 dB。因此,x 1 = 15 英寸处的电压幅值为:
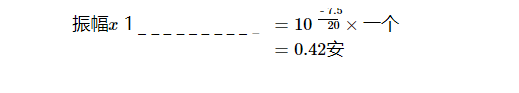
图 2(c) 显示了该有损线路的电压波形。现在让我们通过查看特定时刻 t=t 1的波形来检查波形对位置的依赖性。在这种情况下,项 ?t 变成常数相位项。对于无损线路 (?=0),电压信号变为位置 x 的正弦函数,如图 3(a) 所示。
无损和有损传输线的幅度
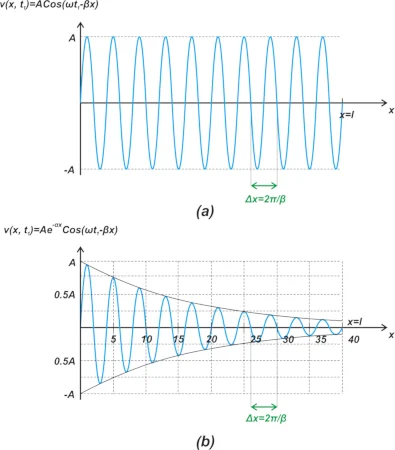
图 3.无损和有损传输线的正弦信号幅度
在图 3(a) 中,电压水平沿线的不同点发生变化,但变化幅度是恒定的,并且对于所有 x 值都等于 A。这与图 3(b) 所示的有损情况形成对比。在此图中,假设线路具有 0.5 dB/英寸的衰减。当我们远离
信号源时,正弦波形的幅度呈指数减小(由于 e -?x 项)。请注意,线路衰减随长度线性增加。例如,如果线路每长度的衰减为 0.1 dB/英寸,则 5 英寸长线路末端的衰减将为 0.5 dB。现在要问的问题是,有损线对方波有何影响?