数字信号的带宽和上升之前的关系

    带宽是用于描述电路行为的常见频域参数。例如，我们通常考虑使用 3 dB 带宽来描述滤波器或通信通道的频率响应。如图 2 所示，低通滤波器的 3dB 带宽是直流传递函数幅度 3 dB 以内的频率响应的一部分（在该图中，直流幅度为 0 dB，并且下降到 -传输函数带宽远端 3 dB）。

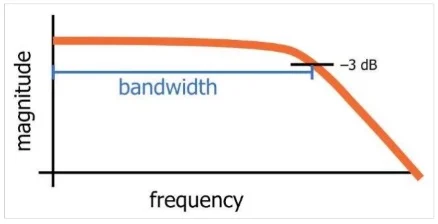
    图 2. Robert Keim 通过AAC创建的图像
    虽然上述带宽定义描述了电路的行为，但还有另一种带宽定义描述了数字信号的频率内容。该定义指定了数字信号频谱内容中的有效频率分量。
    我们将在一分钟内解释该定义中使用的“显着”一词，但在此之前，理想方波的带宽是多少？50% 占空比理想方波（上升/下降时间为零）的频谱内容包括其基频的所有奇次谐波。对于这个理想的方波，带宽是无限的。

    然而，我们在现实世界中无法拥有这种理想信号，因为产生该信号的设备或用于传输该信号的互连将不可避免地表现出有限的带宽。因此，高于我们设备/互连的 3 dB 频率的所有谐波都将被衰减。由于这些高频谐波被抑制，我们将不再有零上升时间方波。相反，我们将得到一个类似梯形的波形，需要一些时间从低电平过渡到高电平，反之亦然。下面的图 3 将梯形信号与理想方波进行了比较。

    图 3. 图片由信号和电源完整性简化提供。
    上图还显示了两个信号的频率内容。正如您所看到的，梯形波形频谱中的高频谐波显着衰减（与理想方波相比）。由于梯形波形不具有高频分量，因此它不能具有表现出急剧转变所需的快速变化。
    如上所述，理想的方波具有无限带宽，但是上述梯形波的带宽是多少？受人尊敬的 PCB 设计师 Eric Bogatin 所著的《Signal and Power Integrity-Simplified》一书建议，与梯形波形（具有任意上升/下降时间）的频率分量相比，如果梯形波形（具有任意上升/下降时间）的频率分量的幅度衰减大于0.7理想方波的相同谐波，则该频率分量被充分衰减并且不是信号频谱中的重要频率分量。仅考虑重要的频率分量，我们可以找到给定梯形波形的带宽。
    例如，通过目视检查图 3，我们观察到 7 次谐波衰减大于 0.7（与理想方波的相同谐波相比）。因此，这个谐波并不重要。然而，根据上述定义，五次谐波似乎很重要。因此，该梯形波形的带宽从直流延伸至五次谐波。如果波形周期为 10 ns，基波谐波将为 100 MHz，带宽将为 500 MHz。
    上升时间和带宽
    我们在实践中看到，上升时间不可能为零。梯形波形的非零上升/下降时间对应于频域中的有限带宽。有一个近似值将信号的上升时间与其带宽联系起来：
    \[BW = \frac {0.35}{T_r}\]

    在此等式中，\[T_r\] 是信号的 10-90% 上升时间。10-90% 上升时间是信号从其终值的 10% 上升到其终值的 90% 所需的时间间隔。例如，如果信号的上升时间为 0.5 ns，则其带宽将为 700 MHz。

上升时间和带宽

我们在实践中看到，上升时间不可能为零。梯形波形的非零上升/下降时间对应于频域中的有限带宽。有一个近似值将信号的上升时间与其带宽联系起来： 

BW=0.35TrBW=0.35Tr

在此等式中，$$T_r$$ 是信号的 10-90% 上升时间。10-90% 上升时间是信号从其终值的 10% 上升到其终值的 90% 所需的时间间隔。例如，如果信号的上升时间为 0.5 ns，则其带宽将为 700 MHz。 

 

互连如何改变信号上升时间？

在本文的部分，让我们简单看一下一个有趣的问题。

如果我们将具有给定上升时间 $$T_{r,in}$$ 的信号通过带宽 BW 的电路，会发生什么？电路的有限带宽如何影响信号上升时间？

例如，假设我们通过一条 4 英寸长、带宽为 BW 的传输线传递信号。如果 BW 足够低，它可以抑制输入信号的某些频率分量并使它们变得微不足道（我们上面解释了在这种情况下显着的含义）。

由于一些高频分量被抑制，信号上升时间会随着到达互连的远端而增加。因此，低带宽电路/互连可以增加信号的上升时间。

下面的等式使我们能够量化这种影响：

$$T_{r,out}=\sqrt{T_{r,in}^2+T_{r,system}^2}$$

这里，$$T_{r,out}$$ 是互连输出处的上升时间，$$T_{r,system}$$ 是与互连相关的上升时间。互连上升时间可以使用上一节中讨论的方程从其带宽中获得。例如，如果互连的带宽为 6 GHz，我们可以将 58.3 ps（皮秒）的上升时间与该互连关联起来。现在，如果我们将 $$T_{r,in}=50ps$$ 的信号发送到该互连，则信号的上升时间将在互连的远端增加到 76.8 ps。

您可以在《CMOS射频集成电路设计》一书的8.5.3节中找到上述方程的数学推导。不幸的是，这个方程的推导并不那么简单。请注意，我们可以轻松扩展该方程来计算 N 个级联系统输出的上升时间。

结论

在本文中，我们讨论了对时域和频域的洞察如何使我们能够更轻松地理解电路的行为。我们研究了信号的上升时间和带宽之间的关系。我们看到信号的上升时间与其带宽成反比，并且这两个参数的乘积始终约为 0.35。我们还看到，当信号通过带宽有限的系统时，其上升时间会增加。