什么是过滤器？

    滤波器是一种去除或“滤除”指定范围的频率分量的电路。换句话说，它将信号的频谱分为将通过的频率分量和将被阻止的频率分量。

    如果您没有太多频域分析经验，您可能仍然不确定这些频率分量是什么以及它们如何共存于不能同时具有多个电压值的信号中。让我们看一个简短的例子，这将有助于阐明这个概念。

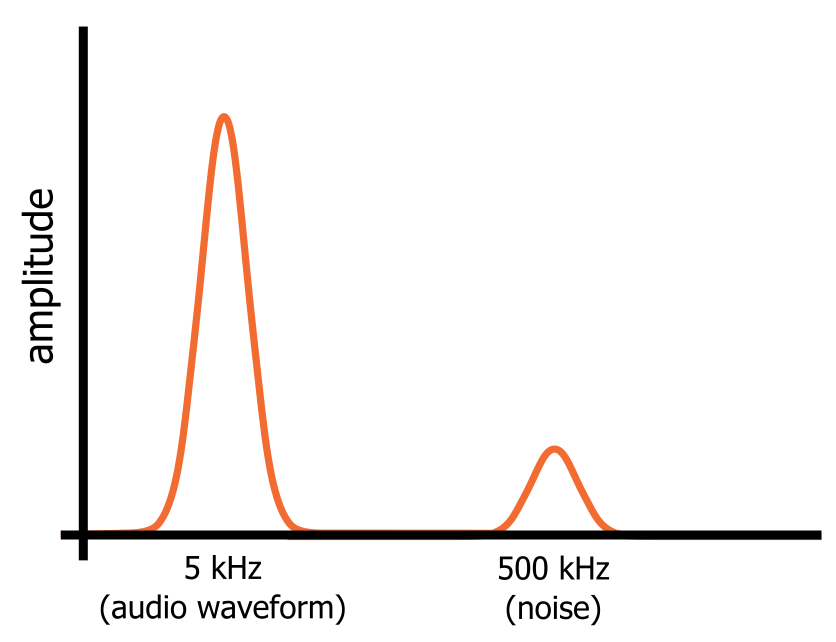
    假设我们有一个由完美的 5 kHz 正弦波组成的音频信号。我们知道正弦波在时域中是什么样子，而在频域中我们只会看到 5 kHz 处的频率“尖峰”。现在假设我们激活一个 500 kHz 振荡器，它将高频噪声引入到音频信号中。

    在示波器上看到的信号仍然只是一个电压序列，每个时刻都有一个值，但信号看起来会有所不同，因为它的时域变化现在必须反映 5 kHz 正弦波和高频噪声波动。

    然而，在频域中，正弦波和噪声是同时存在于该信号中的独立频率分量。正弦波和噪声占据信号频域表示的不同部分（如下图所示），这意味着我们可以通过引导信号穿过低频并阻止高频的电路来滤除噪声。

    过滤器的类型

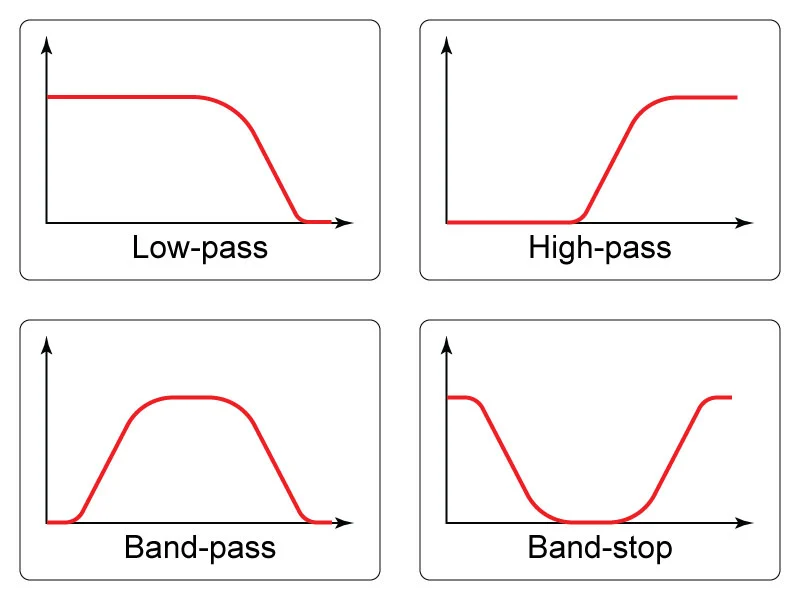
    滤波器可以分为与滤波器频率响应的一般特征相对应的广泛类别。如果滤波器通过低频并阻止高频，则称为低通滤波器。如果它阻止低频并通过高频，则它是高通滤波器。还有带通滤波器和带阻滤波器，带通滤波器仅通过相对较窄的频率范围，带阻滤波器仅阻止相对较窄的频率范围。

    滤波器还可以根据用于实现电路的组件类型进行分类。无源滤波器使用电阻器、电容器和电感器；这些组件没有能力提供放大，因此无源滤波器只能维持或降低输入信号的幅度。另一方面，有源滤波器既可以过滤信号又可以应用增益，因为它包括晶体管或运算放大器等有源组件。

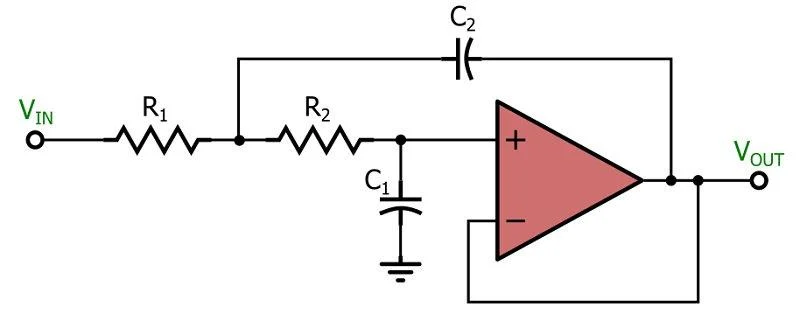
    该有源低通滤波器基于流行的 Sallen-Key 拓扑。

    本文探讨了无源低通滤波器的分析和设计。这些电路在各种系统和应用中发挥着重要作用。

    RC 低通滤波器

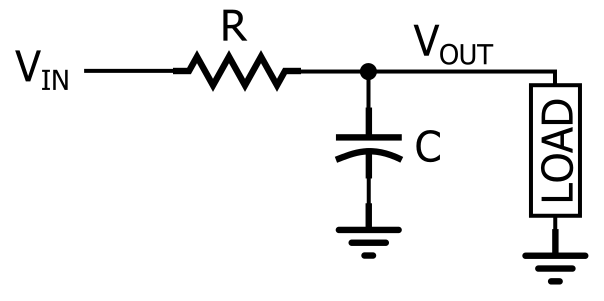
    为了创建无源低通滤波器，我们需要将电阻元件与电抗元件结合起来。换句话说，我们需要一个由电阻器和电容器或电感器组成的电路。理论上，电阻电感（RL）低通拓扑在滤波能力方面与电阻电容（RC）低通拓扑等效。但实际上，电阻电容版本更为常见，因此本文的其余部分将重点介绍 RC 低通滤波器。

    RC 低通滤波器。

    如图所示，RC 低通响应是通过将一个电阻器与信号路径串联以及一个电容器与负载并联来创建的。在图中，负载是单个组件，但在实际电路中，它可能要复杂得多，例如模数转换器、放大器或用于测量的示波器的输入级滤波器的响应。

    如果我们认识到电阻器和电容器形成了频率相关的分压器，我们就可以直观地分析 RC 低通拓扑的滤波作用。

    重新绘制了 RC 低通滤波器，使其看起来像一个分压器。

    当输入信号的频率较低时，电容器的阻抗相对于电阻器的阻抗较高；因此，大部分输入电压在电容器上（以及与电容器并联的负载上）下降。当输入频率较高时，电容器的阻抗相对于电阻器的阻抗较低，这意味着电阻器上压降的电压较多，传输到负载的电压较少。因此，低频被通过而高频被阻挡。

    对 RC 低通功能的定性解释是重要的步，但当我们需要实际设计电路时，它并没有多大帮助，因为术语“高频”和“低频”非常模糊。工程师需要创建能够通过和阻止特定频率的电路。例如，在上述音频系统中，我们希望保留 5 kHz 信号并抑制 500 kHz 信号。这意味着我们需要一个在 5 kHz 到 500 kHz 之间从通过过渡到阻塞的滤波器。