我们可以使用几种不同的规格来表征数据转换器的性能。根据应用的不同,其中一些规范可能比其他规范更重要。
本文着眼于 DAC 的 DNL(微分非线性)和 INL(积分非线性)规范。这些规格在测量和控制应用中通常很重要,在这些应用中通常存在来自理想传输特性的误差预算。
数模转换器 (DAC) 接收表示为数字代码的数据并产生等效的模拟输出(参见下面的图 1)。

上述理想传递函数对应于一个三位单极性 DAC。可以使用Kelvin Divider或R-2R架构等多种结构 来获得上述输入输出特性。
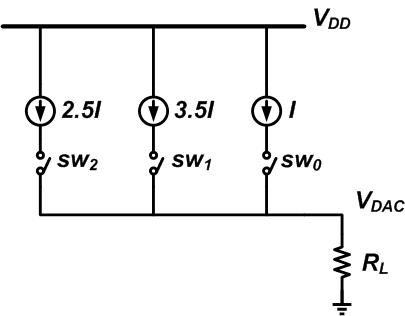
为了说明 DNL 和 INL 规范,我们将考虑一个简单的基于电流源的结构,如图 2 所示。

这个三位 DAC 使用二进制加权电流源来产生图 1 中的八个不同的模拟电平。这里,I 是可以在 DAC 输出中产生电压阶跃的单位电流。因此,sw 0和sw 2分别对应于输入代码的有效位(LSb)和有效位(MSb)。
例如,如果输入数字代码为 101,则开关 sw 0和 sw 2导通,负载电流为 I + 4I = 5I。这会产生等于 5I ? R L的输出电压。同样,输入数字代码的其他组合将产生图 1 的八个不同级别之一。
上述图 2 中的三位 DAC 模型过于理想化;实际上,有许多因素限制了系统的准确性。例如,虽然我们想要一组二进制加权的电流源,但电流源的值可能与图 2 中的略有不同。
图 3 显示了一个夸张的。
这种非理想 DAC 的输入输出特性如图 4 所示。理想情况下,输出电压电平应位于虚线上;然而,由于不匹配,我们得到了实心点表示的电压电平。

DAC 的 DNL 和 INL 规格使我们能够表征这种非理想的输出电压电平。
对于理想的传输特性,如果我们将输入数字代码增加 1,则模拟输出应增加对应于 1 LSb 的模拟值。
例如,如果图 2 的输入代码从 001 变为 010,则输出应从 I ? R L变为 2I ? R L。这两个级别之间的差异是 I ? R L,即一个 LSb 的模拟值。但是,如果我们将图 4 的数字代码从 001 更改为 010,则输出将从 I ? R L更改为 3.5I ? R L。在这种情况下,生成的水平之间的差异是 2.5I ? R L。
DNL 规范是一种表征 DAC 产生的两个连续电压电平之间差异的方法。DNL 是输出阶跃与理想模拟 LSb 值的偏差。
例如,考虑从 001 到 010 的转换,我们得到 2.5I ? R L的输出步长。此步骤与一个 LSb 值的偏差为 2.5I ? R L - I ? R L = 1.5I ? R L。因此,此转换的 DNL 为 1.5 LSb。其他转换的 DNL 如图 5 所示。
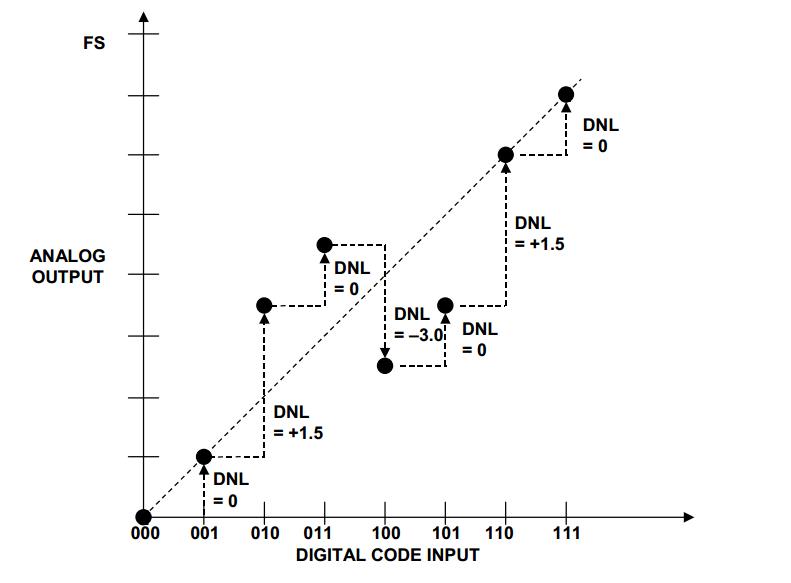
如您所见,对于不同的转换,非理想 DAC 的 DNL 可以为正、负或零。我们通常使用所有转换的偏差的 DNL 来指定 DAC DNL 性能。例如,图 5 输入输出特性的差 DNL 误差为 -3 LSb。
DNL 通常以 LSb 为单位进行测量,尽管我们可以将其测量为(伏特或安培)或满量程值的百分比。
INL 定义为实际输入输出特性与理想传输特性的偏差。理想的传输特性是一条直线穿过原点和全 1 数字代码对应的点(满刻度值减去一个 LSb)。这条线在一些教科书上称为端点拟合线,这种测量INL的方法称为端点法。
在图 5 的示例中,代码 100 的输出 INL 为 -1.5 LSb(理想输出应为 4 LSb,但实际输出为 2.5 LSb)。
值得一提的是,INL 的另一个定义是计算与理想插值线的偏差。这种方法有时被称为“直线法”。通常端点拟合方法,因为它为我们提供了有关 DAC 谐波失真的更多信息。因此,我们将在本文中使用端点匹配定义。
可以通过计算先前转换的所有 DNL 的代数和来找到任何代码输出的 INL。因此,我们有以下关系:
I N L n = n ∑ i = 0 D N L i
例如,代码 100 的输出的 INL 等于 0 + (+1.5) + 0 + (-3) = -1.5 LSb。由于 INL 表征与理想传输曲线的偏差,因此它有点类似于放大器的线性误差。与 DNL 一样,INL 通常以 LSb 为单位进行测量,尽管我们可以将其测量为(伏特或安培)或满刻度值的百分比。
在本文的其余部分,我们将探讨 DNL 和 INL 指标之间的关系。我们将考虑一个简单的基于一元加权电流源的结构(如图 6 所示)来讨论这些概念。
图 2 显示了基于二进制加权电流源的 DAC。我们可以使用相同值的电流源来实现 DAC,而不是使用二进制加权电流源。这种方法使用基于一元加权电流源的结构,如图 6 所示。
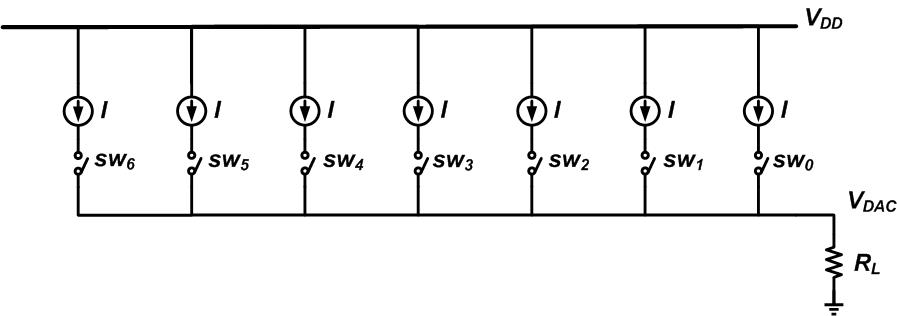
在这种情况下,应打开适当数量的开关以产生给定的模拟电压电平。例如,如果输入数字代码为 101,我们可以打开前五个开关(sw0 至 sw4)并产生 5I 的负载电流。请注意,需要一个数字电路将二进制 DAC 输入代码转换为打开开关的适当代码。
随着二进制输入代码的增加,我们可以按任何顺序打开电流源。然而,简单的方法是按从右到左的顺序打开电流源。换句话说,随着数字输入代码的增加,开关 sw0、sw1、…、sw6 依次打开。
就像二进制加权版本的情况一样,一元加权 DAC 的电流源可能会偏离理想值。电流源阵列可能会出现两种类型的误差:随机误差和系统误差。为了更好地理解这些误差,假设使用单个 PMOS 晶体管来实现图 6 中的每个电流源。如图 7 所示。

在该图中,V b代表偏置电压,并且晶体管具有相同的尺寸。虽然需要相同的电流源,但我们会有略微不同的电流。这是因为许多制造参数实际上是随机变量。例如,IC 制造过程中使用的不同层的边缘表现出随机变化。或者,杂质的扩散涉及晶圆上的随机性。由于这些随机变化,我们预计晶体管电流之间会失配。
除了这些随机变化之外,还可能存在系统误差。
这些系统误差的示例如图 8 所示。
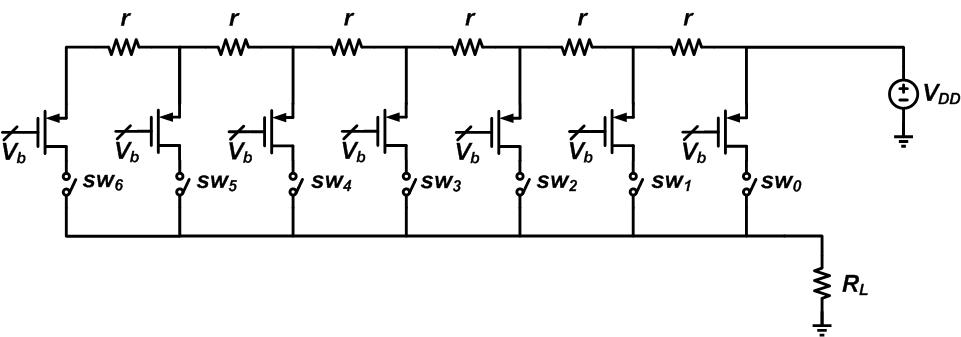
该数字包括将 VDD 连接到晶体管的导线的电阻。每个晶体管的电阻不同,因此 VDD 的压降也不同。因此,即使晶体管 100% 相同,它们的电流也会略有不同。请注意,这不是随机错误。
考虑到上一节的讨论,我们可以将每个 DAC 转换的 DNL 误差分解为两部分:相关项(? corr,由系统误差引起)和不相关项(? uncorr,由随机变化引起)。因此,我们有
我们知道特定输出电平的 INL 是所有先前 DAC 转换的 DNL 的运行总和。DNL 的不相关项的总和看起来像一个噪声项,并且会增加 DAC 输出频谱的本底噪声(我们会降低信噪比)。相关项的总和可以累积并产生相当大的 INL 值。较大的 INL 将导致谐波失真(在 DAC 输出频谱中,我们将有谐波分量而不是增加的本底噪声)。
如您所见,大 DNL 不一定伴随着大 INL,因为如果 ? uncorr比 ? corr大得多,我们就不应该有大 INL。在这种情况下,较大的 DNL 可被视为额外噪声的来源。
上面我提到,我们可以从右到左依次打开/关闭图 6 的电流源(随着数字输入代码的增加,开关 sw0、sw1、...、sw6 依次打开)。有一些技术可以动态改变打开/关闭电流源的顺序。使用此类技术,我们可以实现伪随机顺序,从而减少 DNL 误差的系统分量。这可以有效地提高 DAC 的线性度。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。