控制系统简介：使用 MATLAB 的 SISO 工具设计 PID 控制器

时间：2023-06-08

控制系统工程至少需要了解系统的两个基本组成部分：描述系统数学建模行为的设备，以及您试图达到的目标的输出。巡航控制系统已成为汽车行业中司空见惯的控制系统：输出由驾驶员编程，控制系统必须管理所有车辆读数以保持速度。

因为我们行驶的道路有缺陷，有时系统会自动加速或减速。如果您曾经在汽车上使用过此功能，您可能会注意到汽车会以您选择的速度保持非常平稳的速度 - 它不会突然加速或减速。这意味着车辆的控制系统首先获得所需的输出，然后通过补偿输入（例如，通过向发动机提供多少燃料）来管理实际输出的误差。
在解决系统问题之前，我们将简要分析系统（未补偿）的组件和行为，然后分析 PID（比例-积分-微分）控制器的各个组件。一步是将这两者结合起来并设计一个 PID 控制器来补偿初观察到的系统。重要的是要知道 PID 控制器不是设计人员可以应用于系统的补偿类型，但它是一个很好的起点，可以开始学习一些在其他方法中仍然适用的通用特性。

注意：在本教程中，我们将在理想条件（无噪声或干扰）下分析模拟系统，所有或大部分数学分析将通过 MATLAB 完成。

观察系统

一个系统可以由以同样不同的方式排列的各种组件组成；但我们将从分析经典闭环系统的组件和功能开始（图 1）。

图 1 - 单输入单输出系统闭环系统的示例框图。

输入： r - 输入是某种参考值，应该与系统的输出直接相关。这不一定直接转换为电压/电源，而是将电压/电源连接到系统的设置或开关。在我们稍后分析的系统示例中，我们的输入信号将是单一步骤。
控制器： C - 在我们的例子中，这是我们将设计的 PID 控制器。它位于我们要补偿的设备之前，就在输入信号和反馈的连接点之后。
Plant： G - 这是您所有的子系统，在数学上表示为传递函数。如果您试图控制的是直流电机，那么设备实际上就是您的直流电机。您的输入将使工厂以一种方式做出反应，从而提供接近您的输入的输出值。
输出： y - 该读数是实际系统对我们期望的响应（输入）的响应，该响应已通过我们组装的系统（工厂）。系统的性能是通过输出与输入的比较来判断的，假设会发生某些错误并且已被认为是可以接受的。
反馈： H - 在系统的等效框图（见图 1）中，反馈线将系统的输出引入输入。这意味着可以测量输出（实际响应）和输入（期望响应）之间的任何差异 - 换句话说，输入和输出之间的误差是引入控制器的误差。我们系统的误差等于：输入 - 输出 x H；如果系统有单一反馈（即 H = 1），那么我们的误差就是输入减去输出。当我们继续描述 PID 控制器的每个方面如何工作时，这将是一个重要的想法。
重要的是要注意，通过使用闭环传递函数，图 1 中完整环路的传递函数可以进一步简化为具有单个输入和单个输出的一个块：

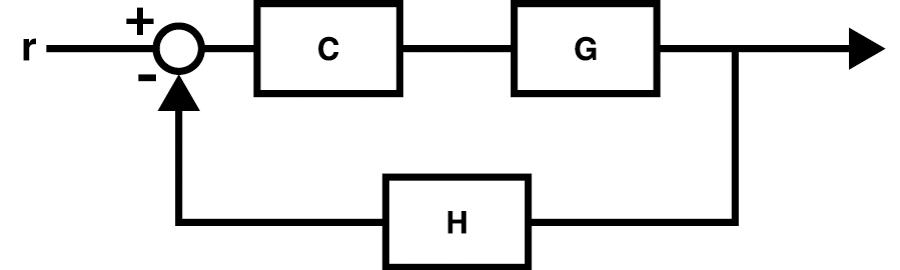
闭环(s)=C(s)?G(s)1+C(s)?G(s)?H(s) $闭环 (s) = \frac{C (s) ? G (s)}{1 + C (s) ? G (s) ? H (s)}$

PID 控制定义

PID 控制器实际上是一个三部分系统：

比例补偿：比例补偿器的主要功能是引入与系统输出和输入比较产生的误差读数成比例的增益。
微分补偿：在酉反馈系统中，微分补偿器会引入误差信号乘以增益 $K_{D}$ 的导数。换句话说，误差信号波形的斜率将引入到输出中。其主要目的是改善整个闭环系统的瞬态响应。
积分补偿：在单一反馈系统中，积分补偿器将引入误差信号乘以增益 $K_{I}$ 的积分。这意味着误差信号曲线下方的区域将影响输出信号。我们稍后会证明这一点，但重要的是要注意控制器的这一方面将改善整个闭环系统的稳态误差。

赔偿	时域	S域
成比例的	$K_{P} e (t)$	$K_{p}$
衍生物	$K_{D} \frac{d}{d t} e (t)$	$K_{D} s$
不可缺少的	$K_{I} \int_{0}^{t} e (x) d (x)$	$\frac{K_{I}}{s}$

因此，PID 控制器可以在数学上描述为：

赔偿	时域	S域
PID控制器	\[K_{P} e(t)+K_{D}\frac{d}{dt}e(t)+K_{I}\int_{0}^{t}e(x)d(x)\ ]	\[K_{P} +K_{D}s+\frac{K_{I}}{s}=\frac{K_{P}s+K_{D}s^2+K_{I}}{s}\ ]

除了简单之外没有其他原因，人们可以理解为什么在分析或设计类似系统时专门使用 s 域 - 使用分数总是比进行积分和/或导数更容易。如果我们现在将我们描述的 PID 控制器应用到图 1，我们的框图现在将类似于您在下面的图 1.1 中看到的内容。

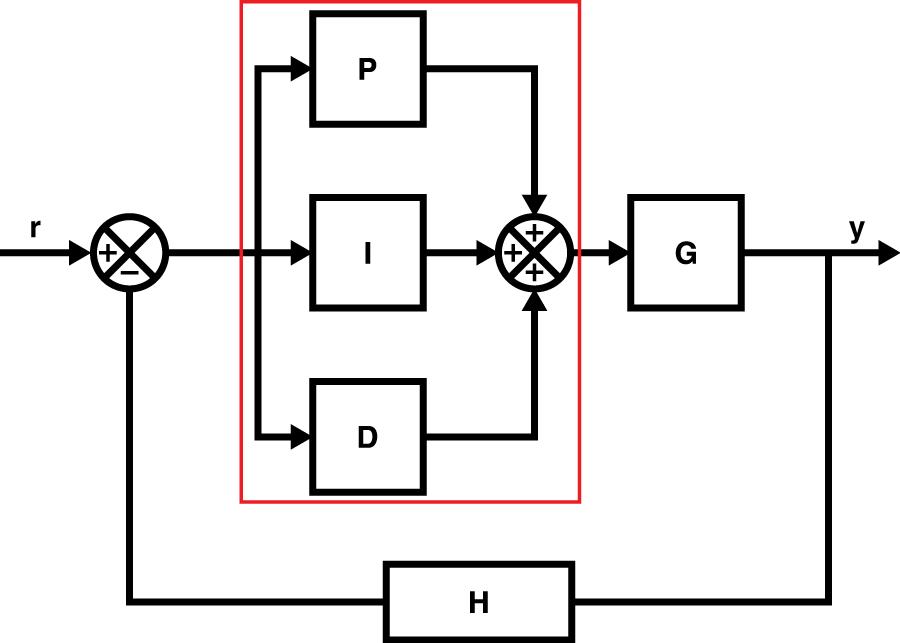
图 1.1 - 我们的“C”块基本上是红色框中包含的所有内容：对系统的比例、微分和积分补偿的总和。

输出特性

现在我们知道系统是由什么组成的以及我们将如何应用 PID 控制器，我们可以开始讨论输出信号的特性（毕竟，这是我们正在监控并试图改变的）

重要方程
输出分析：

特征	方程	描述
一般方程（二阶）	$G (s) = \frac{ω_{n}^{2}}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$	这个一般方程将有助于描述典型的没有零点的二阶函数的行为。然而，并非所有传递函数都是或将是二阶的，并且许多传递函数将包含零。在这些情况下，需要进行部分分数分析以确定在高阶系统上使用二阶方程之间的误差。（注意：对于本文后面使用的示例，我们假设该错误是可以接受的）。
过冲（百分比）	$p O S = e^{? (ζ π / \sqrt{1 ? ζ^{2}})} ? 100$	该值将描述输出波形过冲（或超过）其终/稳态值的百分比。它表示为终值的百分比。
阻尼比	$ζ = \frac{? \ln ? (p O S / 100)}{\sqrt{π^{2} + l n^{2} (p O S / 100)}}$	重要的是要注意阻尼比的方程完全取决于超调量。该比率将描述系统是无阻尼（等于 0）、欠阻尼（在 0 和 1 之间）、临界阻尼（等于 1）还是过阻尼（大于 1）。
高峰时段	$T_{p} = \frac{π}{ω_{n} \sqrt{1 ? ζ^{2}}}$	这是波形达到其值或峰值的时间（以秒为单位）。
稳定时间	$T_{s} = \frac{4}{ζ ω_{n}}$	波形稳定在终/稳态值的 +/- 2% 范围内所需的时间。因为振荡可能会无限期地持续（尽管很小），所以这不需要波形稳定。

稳态误差分析：

$e (\infty) = e_{s t e p} (\infty) = \frac{1}{1 + K_{p}}$ 其中 $K_{p} = lim_{s \to 0} G (s)$

$e (\infty) = e_{r a m p} (\infty) = \frac{1}{K_{v}}$ 其中 $K_{v} = lim_{s \to 0} s ? G (s)$
$e (\infty) = e_{抛物线} (\infty) = \frac{1}{K_{a}}$ 其中 $K_{a} = lim_{s \to 0} s^{2} ? G (s)$

图形表示：

图 1.2 - 该图提供了不同阻尼比如何影响系统输出（响应阶跃）的可视化。这也显示了系统阻尼比和超调百分比之间的直接相关性（阻尼比越小，超调越大）。

图 1.3 - 系统对阶跃输入的响应示例。使用 MATLAB SISO 工具的分析允许用户显示响应的特征 - 在本例中为：峰值时间、过冲和稳定时间。

Matlab 中的控制器设计

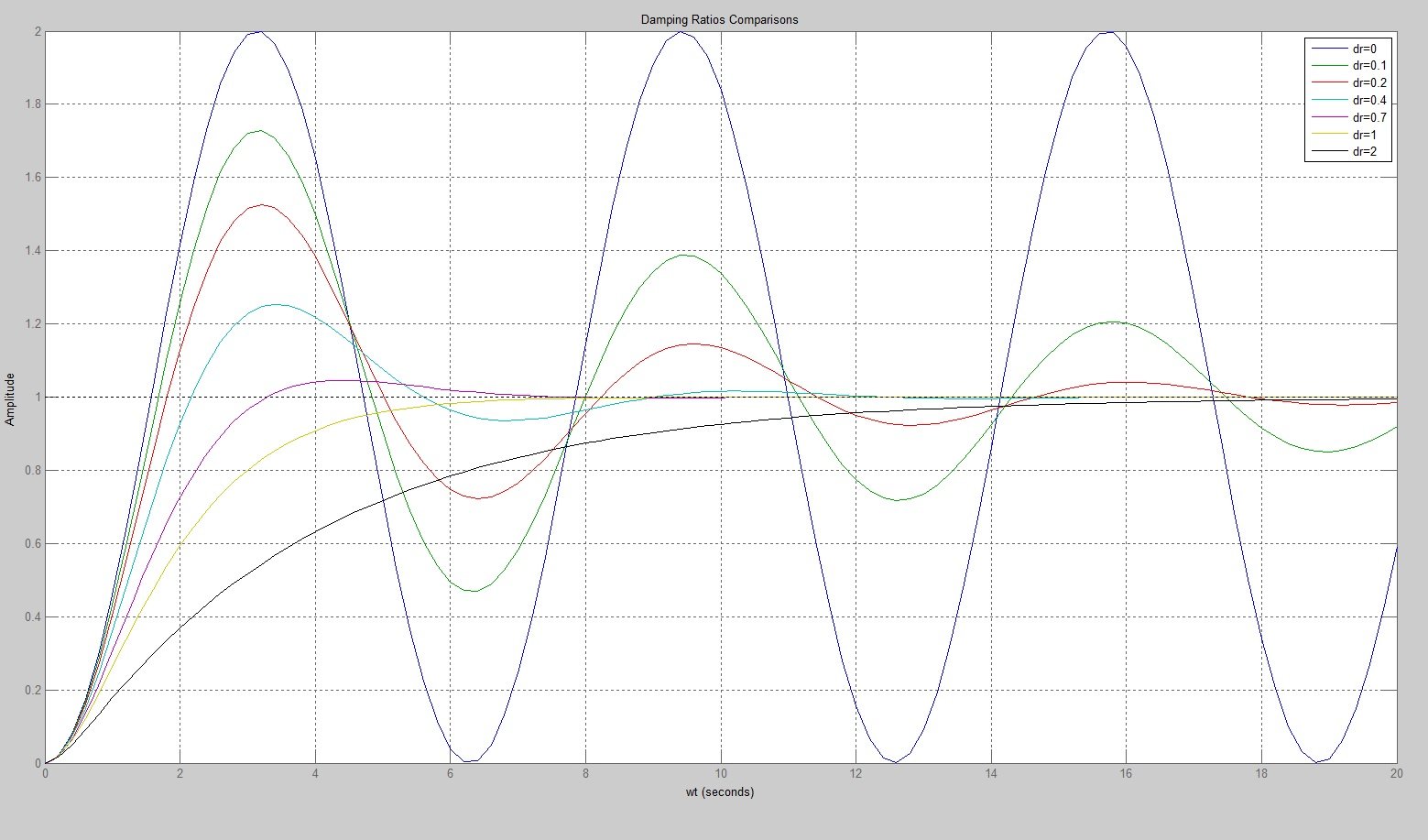
一旦我们拥有需要改进其响应的组件（或工厂）的传递函数，我们就需要做几项改进。MATLAB 包含许多“工程工具箱”，使工程师能够创建、分析和模拟各种不同的项目。在我们的例子中，MATLAB 包含了控制系统工具箱，其中包括为控制系统工程量身定制的几个函数。他们还包括 SISO（单输入单输出）工具，这是一个允许交互式系统分析和控制设计的 GUI。SISO 工具方法的两个方面是：

传递函数的极点和零点的变化如何改变实时响应中的根轨迹和波德图。增益的变化也可以立即反映在系统的阶跃响应中。
指定设计要求将在图形上创建视觉限制，以帮助用户设置和找到适当的增益。这是通过右键单击 SISO 工具根轨迹图并选择“设计要求”来完成的。然后选择要设置的特征类型并定义其限制。这将为您提供定义的边界限制和带阴影的“无效”区域（橙色阴影）。重要的是，作为设计师，您要列出您的优先事项并记下重要的规范。

示例系统传递函数：

$G (s) = \frac{K (s + 8)}{(s + 3) (s + 6) (s + 10)}$

上一篇：SoC 设计：什么时候片上网络 (NoC) 不够用？

下一篇：两种常见的集总参数的衰减器的设计方法