数字信号中上升时间和带宽的关系

使用数字信号时，其带宽与其上升时间/下降时间之间的关系是什么？查看这篇文章以了解更多信息。

在本文中，我们将研究数字信号的上升/下降时间与其带宽之间的关系。在这两个参数（一个来自时域，另一个来自频域）之间建立联系，使我们能够更轻松地分析电路。我们将看到，对这两个域的洞察使我们能够计算信号通过带宽有限的系统时上升时间的增加。

时域和频域

有两种不同的表示法通常用于分析电路的运行：时域和频域表示法。时域分析基于检查电压或电流随时间经历的变化。

另一方面，频域分析将信号表示为具有不同频率的几个正弦波的总和，并检查响应这些频率分量中的每一个的电路行为。

如果我们选择合适的表示法来分析电路，回答特定问题可能会变得更容易。例如，使用时域表示法可以让我们更容易地理解用快速逻辑门驱动相对较长的导线时发生的波反射现象。

然而，例如，如果我们使用频域表示法，则可以更好地分析 PC 板的 EMC 性能。由于在一个或另一个域中回答给定问题可能更容易，因此我们有时需要能够将时域参数转换为频域参数，反之亦然。

在本文中，我们将研究数字信号的上升/下降时间与其带宽之间的关系，这是一个频域参数。但在此之前，让我们看一下一些重要的概念。 

上升时间：一个重要的时域参数

数字信号的上升时间是一个非常重要的时域参数。例如，上升时间会直接影响 PCB 的接地反弹。这在下面的图 1 中进行了说明。
 

图 1.图片由电磁兼容工程提供。

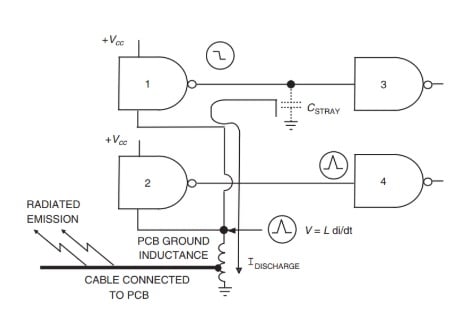
在此图中，接地路径的电感由集总电感器建模。当门 1 的输出从逻辑高变为逻辑低时，存储在 CSTRAYCSTRAY 中的电荷通过接地路径放电。这导致由 $$V=\frac{\Delta I}{\Delta t}$$ 给出的接地反弹，其中 $$\Delta I$$ 是流过接地电感的放电电流，而 $$\Delta t$$是放电时间间隔，与门输出的上升/下降时间有关。

地弹会在门 2 的输出端产生噪声电压，如果足够大，甚至会在门 4 的输出端引起不需要的转换。这只是说明上升时间在高速数字电路中重要性的一个例子设计。我们在之前的文章中讨论过，当驱动具有快速逻辑门的相对较长的导线时，足够小的上升时间会导致波反射现象。  

数字信号的带宽

带宽是用于描述电路行为的常见频域参数。例如，我们通常考虑 3 dB 带宽来描述滤波器或通信通道的频率响应。如图 2 所示，低通滤波器的 3dB 带宽是频率响应的一部分，它位于 DC 传递函数幅值的 3dB 以内（在该图中，DC 的幅值是 0dB，它下降到 - 3 dB 在传递函数带宽的远端）。

图 2. Robert Keim 通过AAC创建的图像

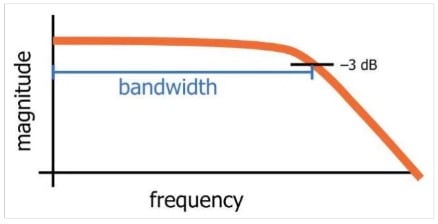
虽然上述带宽定义描述了电路的行为，但还有另一个带宽定义描述了数字信号的频率内容。该定义指定了数字信号频谱内容中的有效频率分量。

我们稍后会解释这个定义中使用的“显着”一词，但在此之前，理想方波的带宽是多少？占空比为 50% 的理想方波（上升/下降时间为零）的频谱内容包括其基频的所有奇次谐波。对于这个理想的方波，带宽是无限大的。 

然而，我们无法在现实世界中拥有这种理想信号，因为产生这种信号的设备或用于传输它的互连将不可避免地表现出有限的带宽。因此，我们设备/互连的 3 dB 频率以上的所有谐波都将被衰减。由于这些被抑制的高频谐波，我们将不再有零上升时间方波。相反，我们会有一个类似梯形的波形，需要一些时间从低到高转换，反之亦然。下面的图 3 比较了梯形信号和理想方波。

图 3. 图片由Signal and Power Integrity-Simplified 提供。

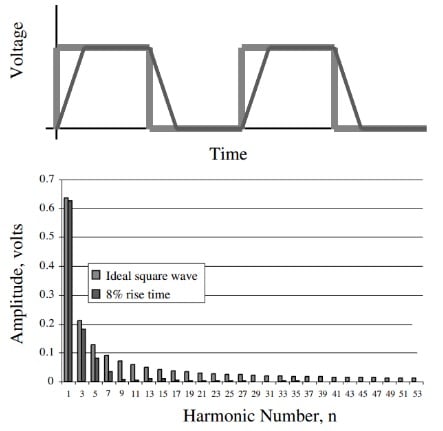
上图还显示了两个信号的频率内容。正如您所看到的，梯形波形频谱中的高频谐波明显衰减（与理想方波相比）。由于梯形波形没有高频成分，因此它不能具有表现出急剧转变所需的快速变化。 

如上所述，理想的方波具有无限带宽，但上述梯形波的带宽是多少？受人尊敬的 PCB 设计师埃里克·博加廷 (Eric Bogatin) 所著的《信号和电源完整性 - 简化》一书建议，如果梯形波形（具有任意上升/下降时间）的频率分量的幅度与波形相比衰减大于0.7倍理想方波的相同谐波，则该频率分量被充分衰减并且在信号频谱中不是重要的频率分量。仅考虑重要的频率分量，我们可以找到给定梯形波形的带宽。

例如，通过目视检查图 3，我们观察到 7 次谐波的衰减系数大于 0.7（与理想方波的相同谐波相比）。因此，这个谐波并不重要。然而，根据上述定义，5 次谐波似乎很重要。因此，此梯形波形的带宽从 DC 扩展到 5 次谐波。如果波形周期为 10 ns，则基波将为 100 MHz，带宽将为 500 MHz。

上升时间和带宽

我们看到，在实践中，我们不可能有零上升时间。梯形波形的非零上升/下降时间对应于频域中的有限带宽。有一个近似值将信号的上升时间与其带宽联系起来： 

$$BW=\frac{0.35}{T_r}$$

在这个等式中，$$T_r$$ 是信号的 10-90% 上升时间。10-90% 上升时间是信号从其终值的 10% 上升到其终值的 90% 所需的时间间隔。例如，如果信号的上升时间为 0.5 ns，则其带宽将为 700 MHz。 

互连如何改变信号上升时间？

在本文的一节中，让我们简要地看一下一个有趣的问题。

如果我们将具有给定上升时间 $$T_{r,in}$$ 的信号通过具有带宽 BW 的电路，会发生什么情况？电路的有限带宽如何影响信号上升时间？

例如，假设我们通过带宽为 BW 的 4 英寸长的传输线传递信号。如果 BW 足够低，它可以抑制输入信号的某些频率分量并使它们变得无关紧要（我们在上面解释了在此上下文中重要的含义）。

由于一些高频分量被抑制，信号上升时间在到达互连的远端时会增加。因此，低带宽电路/互连会增加信号的上升时间。

下面的等式使我们能够量化这种影响：

$$T_{r,out}=\sqrt{T_{r,in}^2+T_{r,system}^2}$$

这里，$$T_{r,out}$$ 是互连输出的上升时间，$$T_{r,system}$$ 是与互连相关的上升时间。互连上升时间可以使用上一节中讨论的等式从其带宽中获得。例如，如果互连的带宽为 6 GHz，我们可以将 58.3 ps（皮秒）的上升时间与该互连相关联。现在，如果我们将 $$T_{r,in}=50ps$$ 的信号发送到该互连，信号的上升时间将在互连的远端增加到 76.8 ps。

您可以在The Design of CMOS Radio-Frequency Integrated Circuits一书的第 8.5.3 节中找到上述等式的数学推导。不幸的是，这个等式的推导并不是那么简单。请注意，我们可以很容易地扩展这个等式来计算 N 个级联系统输出端的上升时间。

结论

在本文中，我们讨论了对时域和频域的洞察如何让我们更容易理解电路的行为。我们研究了信号的上升时间和带宽之间的关系。我们看到信号的上升时间与其带宽成反比，这两个参数的乘积始终约为 0.35。我们还看到，当信号通过带宽有限的系统时，其上升时间会增加。