自然界中各种类型的波的行为基本相似。就像从悬崖上回荡的声音一样,电波在遇到传播介质的阻抗变化时会发生反射。波反射会导致一种有趣的现象,称为驻波。驻波对于大多数乐器发声的方式来说是必不可少的。例如,如果没有驻波的可预测性和放大效应,弦乐器就无法发挥作用。
然而,在 RF 设计中,当我们旨在将功率从信号链中的一个模块传输到下一个模块时,驻波是不可取的。事实上,驻波会影响不同射频和微波系统的性能,从电波暗室 到微波炉等日常电器。
虽然波传播和反射的概念并不十分复杂,但一开始可能会让人有些困惑。可视化波如何从不连续处传播和反射的方法是绘制不同配置的波动方程。
在本文中,我们将首先推导所需的方程式,并使用它们通过几个示例波形来解释驻波现象。
首先,让我们推导出方程式。我知道这很无聊,但它们确实帮助我们了解波是如何在传输线上传播和相互作用的。在本系列的前一篇文章中,我们研究了传输线的正弦稳态响应并推导出了电压和电流方程。将 v s (t) = V scos(ωt) 施加到一条线上,电压和电流波形为:
\[v(x,t)= A cos(\omega t-\beta x) + B cos(\omega t+\beta x)\]
\[i(x,t)=\frac{A}{Z_0} cos(\omega t-\beta x)- \frac{B}{Z_0} cos(\omega t+\beta x)\]
在哪里:
这些等式对应于图 1(a) 中所示的配置,其中选择正 x 轴方向为从源到负载。如果我们用它们的相量表示这些波,则向前传播(或入射)波和向后传播(或反射)的电压波将分别为 Ae -jβx 和 Be jβx,如图 1(a) 所示。
对于传输线问题,通常选择负载到源的正轴方向更方便,如图1(b)所示。为了找到新的方程,我们需要用 ld 替换原始方程中的 x。如新变量 d 所示,向前行进的波变为:
\[Ae^{-j \beta x} = Ae^{-j \beta (ld)}=Ae^{-j \beta l}e^{j \beta d} = A_1 e^{j \beta d }\]
其中 A 1 = Ae -jβl 是一个新常数。从这里,您可以验证,在新的坐标系中,反射波是 B 1 e -jβd,其中 B 1 = Be jβl。因此,总电压和电流相量如公式 1 和 2 所示。
\[V(d)=A_1e^{j \beta d}+B_1e^{-j \beta d}\]
\[I(d)=\frac{A_1}{Z_0}e^{j \beta d}-\frac{B_1}{Z_0}e^{-j \beta d}\]
这些方程可以更容易地检查负载对波反射的影响,因为在这种情况下,负载位于 d = 0,从而简化了方程。令 d = 0,在负载端得到以下方程,如方程 3 和 4 所示。
\[V(d=0)=A_1+B_1\]
\[I(d=0)=\frac{A_1}{Z_0}-\frac{B_1}{Z_0}\]
例如,让我们考虑线路在开路中终止的情况。由于输出开路 (Z L = ∞),输出电流显然为零。根据等式 4,我们有 A 1 = B 1, 因此,总电压为 V(d = 0) = 2A 1。
因此,对于开路线路,反射电压等于输出端的入射电压,此时的总电压是入射电压的两倍。同样,我们可以使用公式 3 和 4 来计算任意负载阻抗 Z L的反射波与入射波之比。这个比率是一个重要的参数,称为反射系数,我们很快就会谈到。
使用等式 1 和 2,我们可以找到沿线不同点的电压与电流(即传输线的输入阻抗)的比率。这导致公式 5。
\[Z_{in}(d) = \frac{V(d)}{I(d)}=Z_0 \frac{A_1e^{j \beta d}+B_1e^{-j \beta d}}{A_1e ^{j \beta d}-B_1 e^{-j \beta d}}\]
注意到线路负载端的线路阻抗 (d = 0) 等于负载阻抗 Z L,我们得到:
\[Z_L = Z_0 \frac{A_1+B_1}{A_1-B_1}\]
使用一点代数,上面的等式给出了反射电压波与入射电压波的比率 (B 1 /A 1 ),它在等式 6 中定义为反射系数 Γ。
\[\Gamma = \frac{Z_L - Z_0}{Z_L + Z_0}\]
上述讨论表明,对于终端线路,入射波和反射波之间存在一定的关系。注意,一般来说,反射系数是复数,Γ的幅度和相位信息都很重要。对于功率传输,我们尝试匹配负载 (Z L = Z 0 ),导致 Γ = 0。在这种情况下,施加到输入端的波完全被负载吸收,不会发生反射。在这里考虑另外两种特殊情况是有启发性的:一条开路线路和一条短路线路,我们将在稍后讨论。
虽然波传播和反射的概念基本上并不复杂,但一开始可能会让人感到困惑。可视化波如何传播和从不连续处反射的方法是绘制我们在上面开发的方程式。此外,值得一提的是,有许多在线模拟器可以帮助您更好地理解波传播概念。
接下来,让我们回顾一下短路线。短路时,总输出电压应始终为零。此外,根据等式 6,我们有 Γ = -1。入射电压波由下式给出:
\[v_i (d,t)=Real \text{ } Part \text{ }of \Big (A_1 e^{j \beta d} e^{j \omega t} \Big ) = A_1 cos(\omega t+ \beta d)\]
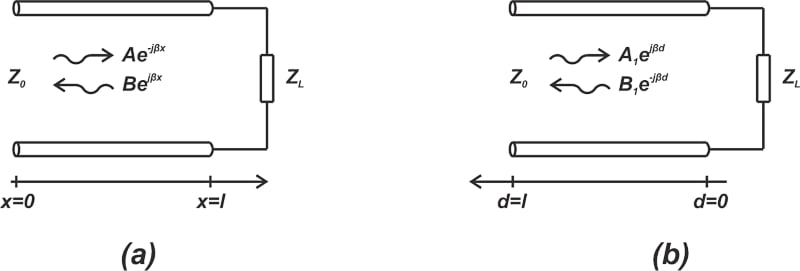
图 2 中的顶部曲线提供了该方程在三个不同时间点 t 1、t 2和 t 3 的曲线图, 其中 t 1 < t 2 < t 3。
上述曲线细分,其中:
请注意入射波如何随着时间的推移逐渐移向负载(在 d = 0 时)。上图中的中间曲线显示了远离负载的反射电压。反射电压方程为:
\[v_r (d,t)=Real \text{ } Part \text{ }of \Big (\Gamma A_1 e^{-j \beta d} e^{j \omega t} \Big ) = A_1 cos( \omega t - \beta d)\]
其中Γ设置为-1以考虑短路。总电压是下方曲线中给出的入射电压和反射电压之和。正向电压在线路的所有点(包括线路的负载端)的值和值之间波动。然而,反射电压取入射电压的相反值,因此负载端的总电压始终为零。
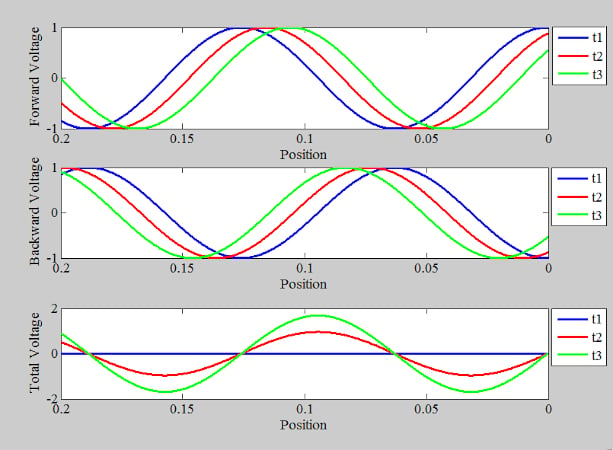
总电压波有一个有趣的特征:它静止不动,与它的组成波不同,总电压波不向任何方向传播。例如,和零电压点不会随时间移动。为了更好地说明这一点,图 3 绘制了 36 个不同时间点的总电压。
可以看出,零交叉点(节点)和幅度的位置(波腹)是沿线的一些固定位置。由于波不向任何方向传播,因此称为驻波。
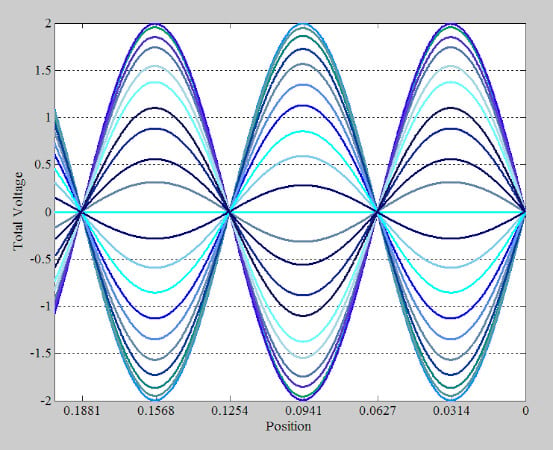
对于开路线路 (Z L = ∞),公式 6 得出 Γ = 1。在这种情况下,反射电压的幅度和相位等于入射电压。图 4 中的顶部和中间曲线分别显示了三个不同时间点开路线路上的入射和反射电压波。
请注意,入射波和反射波在 d = 0 时具有相同的值。因此,总电压(底部曲线)是负载端入射电压的两倍。由于 Γ = 1,反射电流 I r 也与入射电流 I i具有相同的幅度和相位。然而,负载端的总电流为 I i - I r = 0,这并不奇怪,因为负载是开路的。
此外,我们可以再次观察到总电压是一个驻波。这在图 5 中得到了的说明,它绘制了 36 个不同时间点的总电压波形。
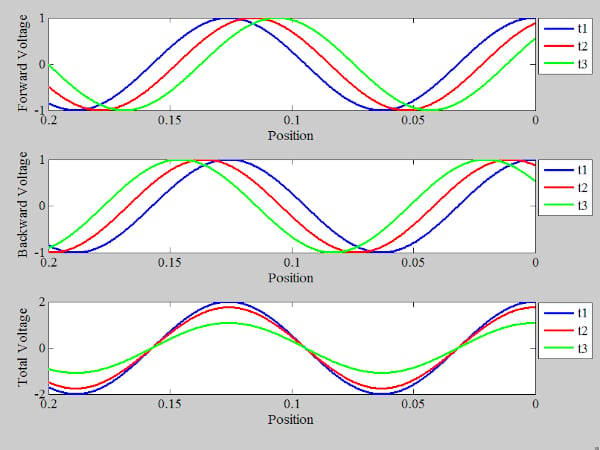
接下来,让我们使用方程来检查 Γ = 0.5 的终止线。图 6 绘制了任意时间的入射和反射电压波。
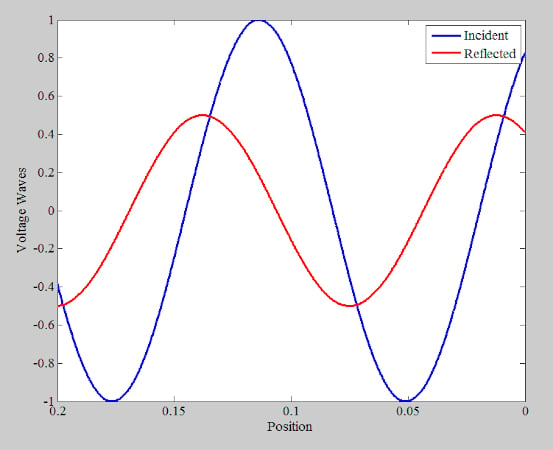
这两个波沿相反的方向传播。你应该可以想象,在某一时间点和沿线的某个特定位置,两个波的峰值会重合,产生总电压波的值。这在图 7 中进行了说明。
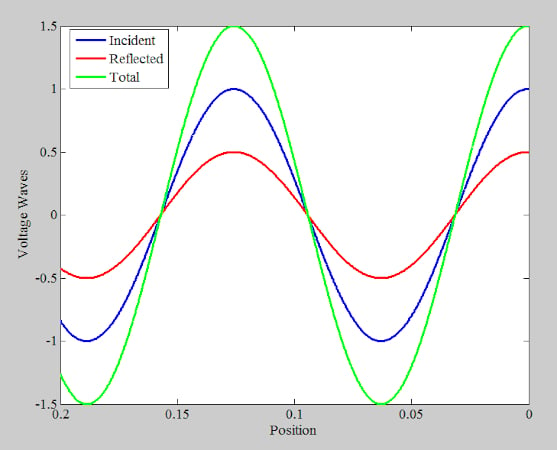
此外,在其他某个时间点,沿线的特定位置将“看到”较大波的峰值和较小波的值,如图 8 所示。
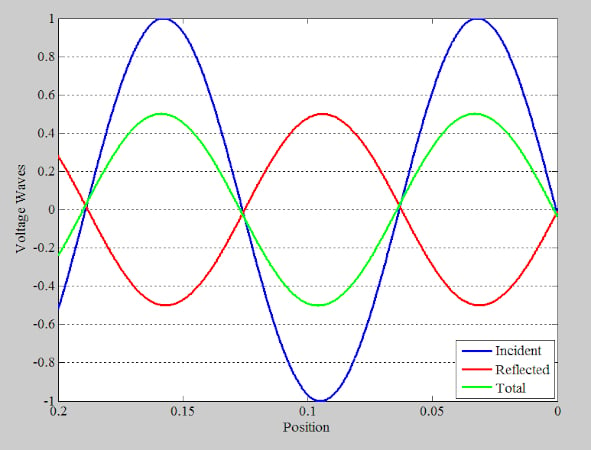
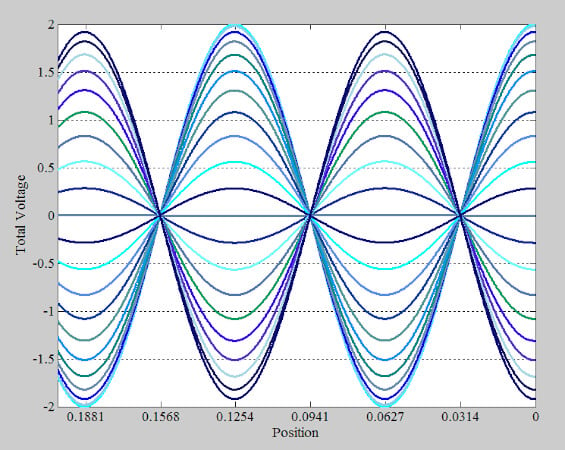
在这些点上,总电压波的幅度处于值。在我们的示例中,前向波和反射波的振幅分别为 1 和 0.5。因此,总电压波的振幅为 1 - 0.5 = 0.5。为了更好地观察沿线不同点的电压幅度,图 9 绘制了 36 个不同实例的总电压波形。
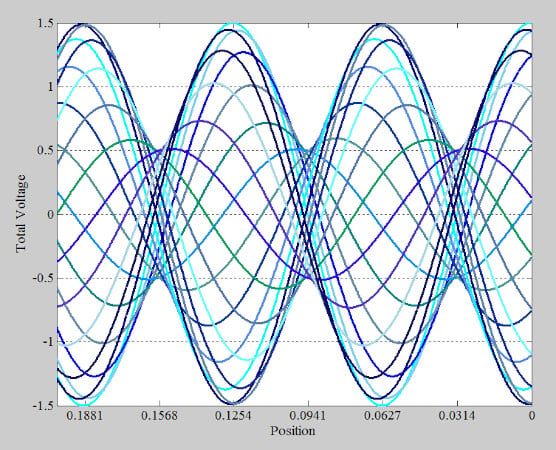
该图让您了解线上不同点的波动幅度。请注意,虽然 d = 0.1881 m 等点在 ±1.5 V 之间波动,但还有其他点。例如,d = 0.1568 m,其振幅要小得多,在±0.5 V 之间波动。
您可能会问的一个问题是,总波是在移动还是静止不动?图 10 显示了一些连续时间点 (t 1 < t 2 < ...< t 6 )的较少数量的总电压图来回答这个问题。
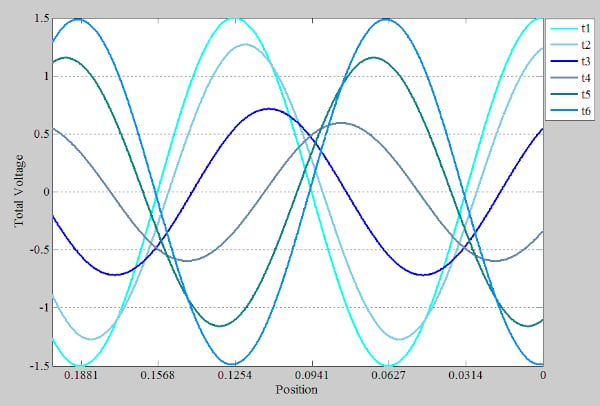
该图显示,随着时间的推移,波向负载传播。请注意,虽然入射波和反射波的幅度是恒定的,但组合电压的幅度会随时间上升和下降。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。