我们经常会在
模拟电路中用到
滤波器,比如音频信号、心电图信号、
传感器等等信号中滤除不想要的信号频段。相对来说,数字信号对噪声的容忍度会高一些,但有时在应用中我们也希望在信号链的某个点滤除不需要的数字波形。
你可能想知道为什么需要某种特殊滤波器来处理数字信号。与对模拟波形进行低通滤波相比,对数字波形进行低通滤波有何不同?
首先,我们先来了解一下傅里叶变换。在频域中,你看到的数字波形实际上并不是数字波形。它是一长串(理论上是无限的)具有不同频率和不同振幅的正弦曲线的组合。当这些正弦波完全对齐时,结果就是一个正常的方形(或矩形)波形。 然而,当它们没有对齐时,你终会得到一个扭曲的块状东西,它不是真正的方波,也不是正弦波。
举一个例子。下面的电路是一个四阶巴特沃斯低通滤波器:
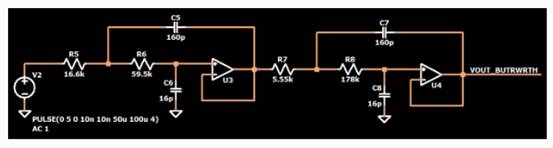
下面是它的频率响应曲线
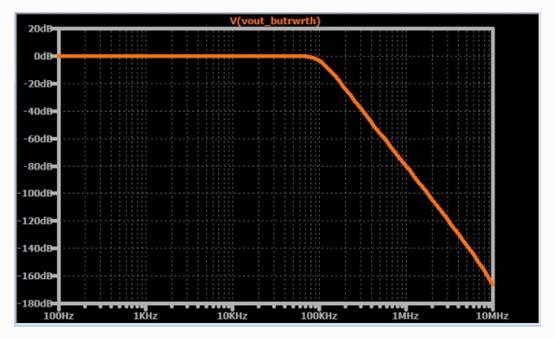
如果我使用此电路过滤 10 kHz方波,结果如下:

这里的问题是巴特沃斯滤波器没有线性相位响应—换句话说,相移以不同频率经历不同时间延迟的方式变化。因此,方波中的频率分量在通过滤波器时不会保持对齐,终结果是我们在上升沿/下降沿看到的过冲/下冲。
上图中出现的过冲并不可怕,但波形的整体外观随着周期的减小而恶化比较严重:

另请注意,随着滤波器阶数的增加,振铃会变得更严重。
我们可以使用贝塞尔滤波器来解决上面这个问题。贝塞尔电路本身与巴特沃斯电路或切比雪夫电路没有什么不同。只是部分
元器件的值发生了改变。
贝塞尔滤波器针对线性相位响应进行了优化,这使其非常适合限度地减少数字信号中的振铃,过冲。我们要记住这种变化的真正原因:非线性相位响应,它会在波形之间产生时间分离构成方波的傅里叶频率。
下面的电路和前面的电路一样有四个极点,和相同的截止频率。 然而不同的是元器件选用了不同的值来创建贝塞尔响应而不是巴特沃斯响应。

下面是波特图
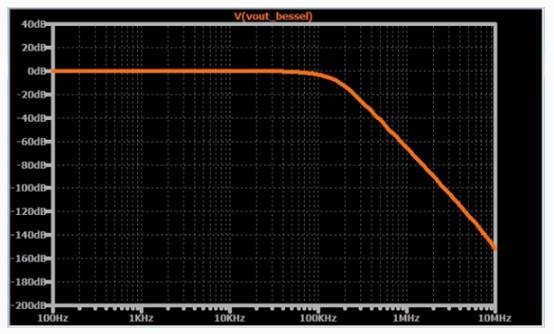
下图包括巴特沃斯和贝塞尔滤波器的时域波形;你可以看到贝塞尔滤波器大大减少了失真。

结论:
我们讨论了数字信号低通滤波的概念,我们研究了没有线性相位响应的滤波器产生的不良影响。,我们引入了贝塞尔滤波器,它针对线性相位响应进行了优化,并且可以显然减小时域波形中的振铃。






