关信号条件的文章中使用了电压激发,但应注意的是,大多数RTD应用程序都使用当前源来激发传感器。图1(a)和(b)分别描绘了电压和当前激发方法的简化图。
电压(a)和电流(b)激发方法的图。

图1。电压(a)和电流(b)激发方法的图。
这两种方法之间的选择是由设计师的酌情决定权。但是,当前的激发可以提供更好的噪声免疫力,并且通常是嘈杂的工业环境中选择的方法。大多数专为RTD应用设计的Delta-Sigma(δ?)转换器包括一个或多个内部电流源用于RTD激发。结果,当前的激发似乎比电压激发更普遍。我们还将很快讨论,使用当前激发时,更容易补偿RTD铅电阻误差。
RTD电阻:电阻误差
铅和接线电阻串联出现与RTD电阻,并将误差引入我们的测量结果中。假设100ΩRTD通过10英尺的线连接到测量系统,该线与传感器的每个引线串联表现出1Ω(0°C)的电阻,如图2所示。
描述铅和布线电阻的示例图。
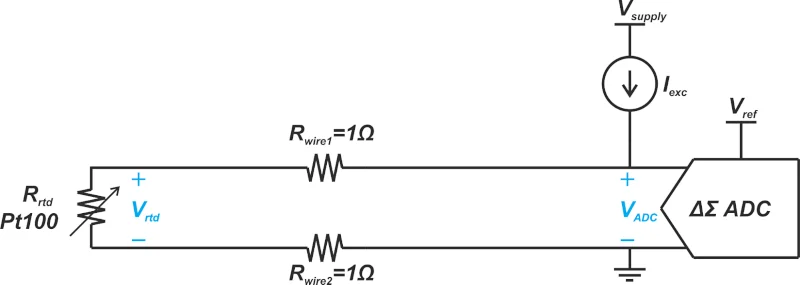
图2。描绘铅和接线电阻的示例图。
在这种情况下,在0°C时, ADC(类似物到数字转换器) “看到”的总电阻 为102Ω。考虑到RTD的温度系数为0.385Ω/°C,接线电阻的误差为5.2°C。实际上,传感器可以远离测量系统,从而导致更大的错误。此外,由于接线电阻随温度而变化,因此误差不是恒定的,不能轻易修剪。
图2中所示的简单接线配置称为两线配置。另外两种接线技术,三线和四线配置,使我们能够补偿接线电阻误差。两线配置是三种可用选项中简单,不准确的。请注意,铅线电阻还会在使用电压激发的图1(a)中所示的电路中产生误差。
RTD三线配置
三线配置如图3所示。
显示三线配置的图。
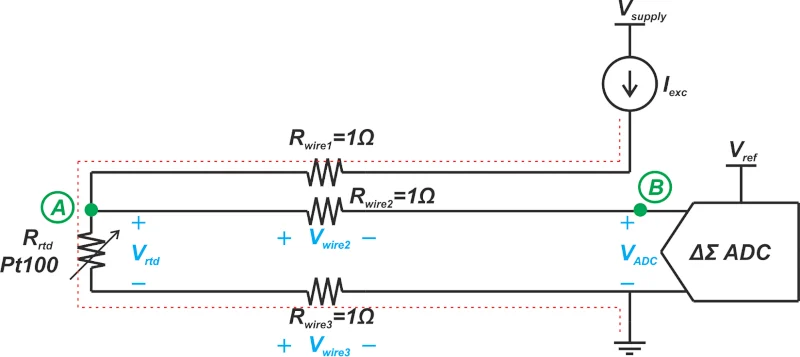
图3。显示三线配置的图。
这种配置需要三根电线将传感器连接到测量设备。红线显示了从测量系统到RTD到系统接地的当前路径。假设ADC输入表现出较高的阻抗,则没有电流可以通过节点A和B之间的电线流动。因此,这两个节点处于相同的电位,即v wire2 = 0。应用Kirchhoff的电压定律,即出现在电压上的电压。 ADC输入被发现为:
\ [v_ {adc} = - v_ {wire2}+v_ {rtd}+v_ {wire3} = v_ {rtd}+v_ {rtd}+v_ {wire3} \]
在这种情况下,仅来自一根电线的电阻在ADC输入处产生误差电压。假设电线具有相同的电阻,上述构型将电阻误差降低了两个。图4显示了如何与电压激发的RTD一起使用三线配置。
带有电压激发的RTD的三线配置示例。
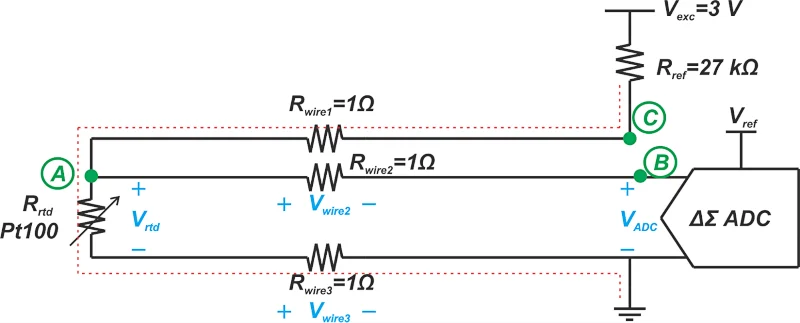
图4。 带电压启用的RTD的三线配置示例。
同样,没有电流流过R Wire2,并且ADC会感觉到RTD上的电压加上R Wire3的电压。这将电阻误差减半。
使用两个当前资源的三线配置
具有恒定电流激发的替代三线配置如图5所示。
具有恒定电流激发的替代三线配置。
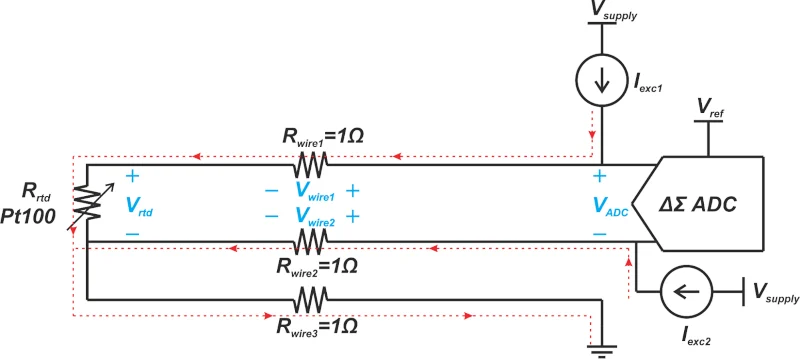
图5。 具有恒定电流激发的替代三线配置。
在这种情况下,使用两个匹配的电流来源来完全消除电阻性误差。应用基尔乔夫的电压法,我们有:
\ [v_ {adc} = v_ {wire1}+v_ {rtd} -v_ {wire2} \] \]
假设当前源和电线电阻是相同的(\(i_ {exc1} = i_ {exc2} \和\,\,r_ {wire1} = r_ {wire2} \)),则在R Wire1和Rire1和R Wire2,我们有V ADC = V RTD。因此,通过ADC测量的电压消除了电阻误差。两种激发电流的总和无害地通过第三线流向系统地面。目标RTD应用程序提供了一些ADC,例如来自模拟设备的AD7711,提供了匹配的电流来源,以促进上述三线配置。
图6显示了AD7711的功能框图,其中包含两个匹配的200μa电流源。
AD7711的框图。
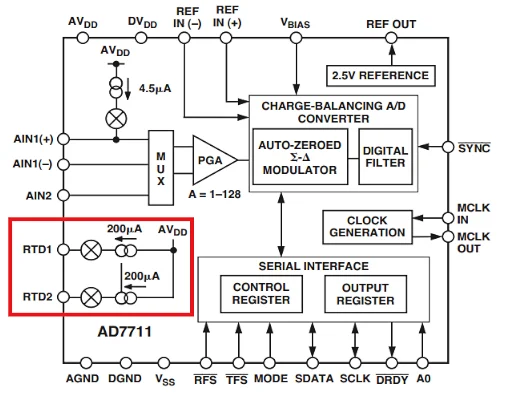
图6。ad7711 的框图。图像由模拟设备提供
图5中的电路假设两个电流源是相同的。两个电流源之间的任何不匹配都允许接线电阻将错误引入系统。解决此问题的一种方法是在输入之间交换两种电流。然后将从这两个配置获得的电压进行平均,以删除当前的不匹配误差。让我们得出方程式以充分了解该技术的工作原理。首先,考虑图5所示的情况,并假定当前的来源不等。通过ADC测量的电压可以找到:
\ [v_ {adc1} = r_ {wire1} i_ {exc1}+r_ {rtd} i_ {exc1} -r_ {wire2} i_ {exc2} \]
如果我们在两个输入之间交换两个电流源(图7),我们将获得一个新的测量值:
\ [v_ {adc2} = r_ {wire1} i_ {exc2}+r_ {rtd} i_ {exc2} -r_ {wire2} i_ {exc1} \]
图显示了两个输入之间两个电流源的交换。
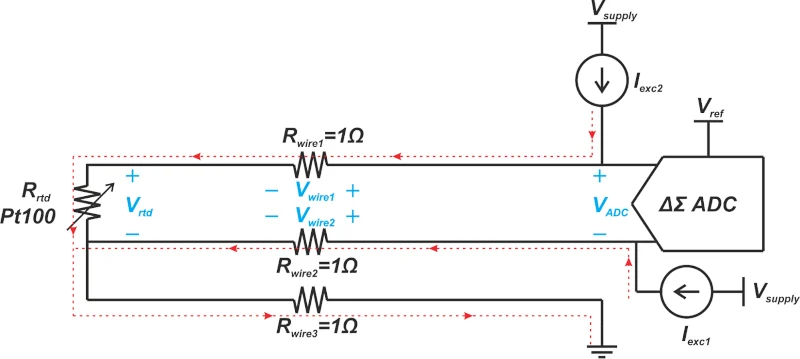
图7。显示两个输入之间两个电流源的互换。
平均两个测量值,我们获得:
\ [v_ {adc,ave} = \ frac {i_ {exc1}+i_ {exc2}}} {2} {2} \ big(r_ {wire1} -r_ {wire2}+r_ {wire2}+r_ {rtd} \ big)\ big)\] \]
如果线电阻是相同的\(r_ {wire1} = r_ {wire2} \),则上述方程式简化为:
\ [v_ {adc,ave} = \ frac {i_ {exc1}+i_ {exc2}}} {2} {2} \ times r_ {rtd} \]
该方程与接线电阻无关。某些ADC(例如ADS1220)旨在关注RTD测量要求,其中包括一个多路复用器来交换内部电流源。图8显示了使用ADS1220的当前交换(或切碎)功能的三线RTD测量图。
带有电流交换的三线RTD测量图。
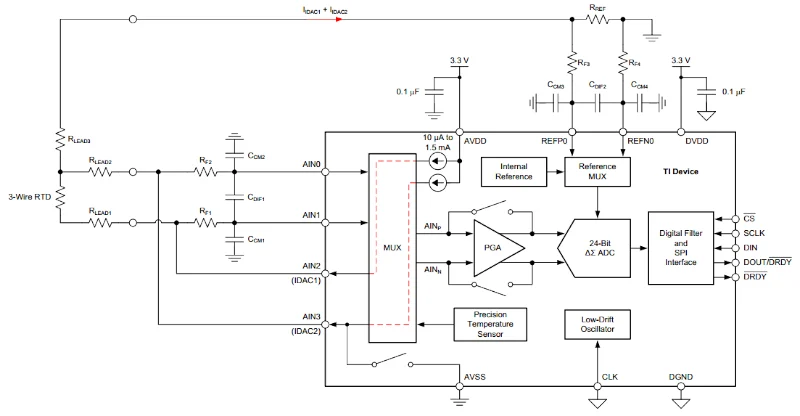
图8。 带有电流交换的三线RTD测量图。图像由Ti提供提高三线电压激发RTD的精度
通过三线配置,可以使用两个匹配的电流源来消除电阻误差。电压激发的三线RTD呢?在这种情况下,是否有一种简单的方法可以完全消除电线阻力错误?我们上面讨论了电压激发的三线路仅将电阻误差减半。我们可以使用下面描述的修改图(图9)来消除电线电阻误差。
示例图,显示了消除电阻误差的图。

图9。示例图显示了消除电线电阻误差。
在这种情况下,合并了一个模拟开关,使我们能够测量节点B和C的电压。节点B处的电压由以下等式给出:
\ [v_ {b} = v_ {a} = v_ {rtd}+v_ {wire3} \]
等式1。
节点C处的电压为:
\ [v_ {c} = - v_ {wire1}+v_ {rtd}+v_ {wire3} \] \]
等式2。
假设电阻是相同的,我们可以得出结论,V Wire3 = -V Wire1。因此,公式2简化为:
\ [v_ {c} = v_ {rtd}+2v_ {wire3} \]
等式3。
将等式1和3组合在一起,我们获得:
\ [v_ {rtd} = 2v_ {b} -v_ {c} \]
如您所见,可以通过测量V B和V C来准确测量RTD的电压降。尽管此技术使我们能够补偿电线电阻误差,但它需要额外的硬件并增加了测量的复杂性。包含匹配电流源的ADC提供了一种方便的解决方案,以消除电阻误差。这就是为什么当前激发比RTD应用中电压激发更普遍的原因。








