数字滤波是频谱、语音和图像处理等应用中的一个基本技术,与模拟滤波相比,数字滤波具有很多突出的优点。数字滤波在性能上可以满足幅度和相位的严格要求,可以避免电压漂移、温度漂移和噪声问题; 在实现上具有稳定性好,高、抗干扰能力强等优点[1]。
当今的数字信号滤波,多采用微处理器ASIC( Applicaon Specific Integrated Circuit) 芯片实现[2]。近年来随着大规模集成电路技术的飞速发展,DSP( Digital Signal Processor) 技术与微处理器技术紧密结合,可以极大地提高系统的运算速度与,使得新一代的具有DSP内核的微处理器成为智能化仪器与设备的元件。但是高性能的DSP 芯片的价格也是昂贵的,在系统开发时必须要考虑到系统的整体成本价格,选择合适的设计方案。DSP 的ASIC 滤波芯片往往应用于专门的领域,如直流电压的高分辨率测量、温度、压力和质量信号的测量等。如何采用灵活的设计方式,低成本地实现数字滤波成为一项挑战[3]。
地震数据采集系统为地质勘探服务的仪器,将地面上的震动信号转换为数字形式记录下来,通过对采集的数据进行反演,得到地层的结构。本文针对地震数据采集系统的数字滤波设计提出并实现了一种FPGA( Field Programmable Gate Array) 与MCU( Micro Control Unit)相结合的设计方案,兼顾开发成本和灵活性。方案的思想不仅适用于地震数据采集系统,也适用于电压、压力、音频等各种传感器网络。
在现代地震数据采集的设计中,为了能获得高分辨率的振动信号,不仅数据要求达到24 位,系统测试时信噪比通常要好于110dB[4]。地震数据采集的另一个特点是有效性能量都处于低频部分[5],通常在几百赫兹以下,因此终只需要1 kHz /s 的数据采样率[6]。
Sigma - Delta 转换器以远远高于奈奎斯特采样率对模拟信号进行过采样,非常适用于频率低于数千赫兹的缓慢变化信号的高A/D 转换。目前在地震数据采集中广泛应用的Sigma - Delta A/D 转换器主要有Cirrus Logic公司的CS5371 /5372 高24 位A/D 转换器[7]。
根据地震数据采集Sigma - Delta 高度过采样的特点,需要在后端设计一个数字抽取滤波器,对信号进行抽取和调理。需要实现的功能有三个: 一是使调制器输出的高速的信号频率降到奈奎斯特频率; 二是滤除调制器输出的高频噪声; 三是将调制器输出的一位数字信号转换为高的多位数字输出信号[8]。
在将数字滤波器运用于Sigma - Delta A/D转换器中时,理论上既能采用FIR( Finite ImpulseResponse) 数字滤波器,也能采用IIR( Infinite Impulse Response) 数字滤波器来实现。IIR滤波器具有无限长的冲激响应,但是IIR 数字滤波器的相位特性不好控制,对相位要求较高时,需加相位校准网络,因此IIR 数字滤波器是不适合的。FIR 滤波器没有反馈回路,故不存在不稳定的问题,同时可以做到严格的线性相位。由于Sigma - Delta A/D 转换器是一种高、高保真的A/D 转换器,因此除了要保证信号幅度的外,还必须保证信号各频率分量的相对相位不变,否则会产生相位失真[9]。
Sigma - Delta A/D 转换器的高度过采样要求数字抽取滤波器具有很高的抽取率,滤波器采用多级抽取的结构可以获得更高的效率。多级的抽取结构和单级的结构相比,计算量和存储量要求更低,每的归一化带宽较宽,可以减少有限字长效应[8]。此外,由于抽取方式应用时降低了数据率,所以后续工作的FIR 滤波器需要的时钟速率也跟着降低了,能限度地节约高速硬件系统中的功耗。
直接式FIR 滤波器的结构需要很多乘法器和加法器,这样的结构需要较多的面积和成本,所以要想办法减少乘法器和加法器的使用。CIC 滤波器( Cascaded Integrator - Comb Filter)是一种高效计算实现窄带低通的滤波器,它的频率响应曲线跟SINC 函数sin( x) /x 相似,通常被应用在现代通信系统,实现硬件抽取和内插。CIC 滤波器在硬件设计中受欢迎的一个重要的特点是它们不需要乘法,只需要加法和减法,可以降低计算复杂性,便于系统实现[10]。
在CIC 滤波器抽取/插值的应用中,常常希望得到一个平的通带和一个窄的过渡带,但是这跟CIC 滤波器本身的特性是不符合的,为了解决这一问题,CIC 滤波器的前端或者后端通常有一个高性能线性相位低通FIR 滤波器,这些FIR 滤波器的任务是补偿CIC 滤波器的非平坦的传输频带。
图1( a) 所示是一个经典的一阶CIC 滤波器,由延迟单元和加减单元构成。对于一个N阶,时延为D 的CIC 滤波器,其z 域传输函数为:
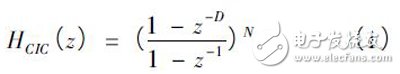
CIC 滤波器有抽取滤波的形式,抽取操作意味着每隔R 个样点只取一个样点输出,从而导致输入采样率是输出采样率的R 倍。梳状滤波器的位置放在抽取之后可以节约计算时需要的寄存器空间。大部分的CIC 滤波器都是采用如图1( b) 所示的结构,此时梳状滤波器的延迟为N = D/R,而不是D。
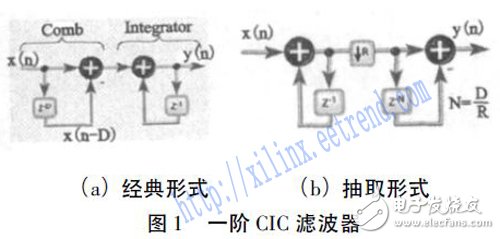
CIC 滤波器的主要特点是延迟累加,所以只要用加法器、减法器和寄存器就能实现,无需乘法器,因此用FPGA 实现起来比软件算法实现要简单,而且由于FPGA 是并行结构,所以处理的速度也比软件处理快,故选用FPGA 来实现CIC 滤波。
FIR 滤波器算法是对具有一组相关系数的输入信号进行离散卷积。一个M 阶FIR 滤波器的变换函数为:
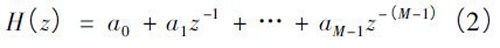
由变换函数的表达式可看出,变换函数实际上需要用乘法器、延时元件及加法器来实现。FIR 也可以使用FPGA 来实现。用FPGA 实现FIR 的优点与实现CIC 一样,处理速度快,但是由于FIR 实现需要用到乘法器,所以实现起来比CIC 复杂,也需要更多的资源,这样对成本控制是不利的。并且在地震数据滤波中,数据速率很低,并不需要高速的FIR 滤波,所以在这里,把FIR 滤波部分由MCU 来完成,在节省硬件资源的同时降低了成本。
滤波系统的整体框图如图2 所示,由FPGA模块、MCU 模块两部分组成。其中CIC 滤波模块在FPGA 内实现,而FIR 滤波在MCU 内实现。
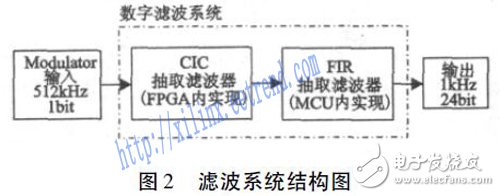
滤波系统的输入信号为正弦信号经过Sigma-Delta ADC 转换后形成的1 bit 数据流,数据率为512 kHz。经过CIC 抽取滤波器和FIR滤波器抽取滤波之后,得到24 位1 kHz 数据率的输出数据。
地震数据采集的采样率除了常用的1 k采样率,还有2 k,4 k 采样率等,为了支持多种采样率,CIC 整体模块由4 个单级的CIC 模块级联形成。在其他采样率时,可以旁路其中部分滤波器。
如图3 所示,这四个单级CIC 滤波器分别是一个5 阶的8 抽样CIC 滤波器( CIC 1) 、一个4 阶的2 抽样滤波器( CIC 2) 、一个5 阶的2 抽样滤波器( CIC 3) 和一个6 阶的2 抽样滤波器( CIC 4) 。Sigma - Delta A/D 转换器输入数据率和位宽分别是512k、1 bit,经过CIC 1 后,位宽17 bit、数据率64 kHz; 经过CIC 2 后,位宽21bit、数据率32 kHz; 经过CIC 3 后,位宽24 bit、数据率16 kHz; 经过CIC 4 后,位宽24 bit、数据率8 kHz。
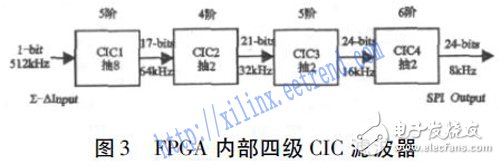
四级CIC 滤波器变换函数H( z) 分别为:
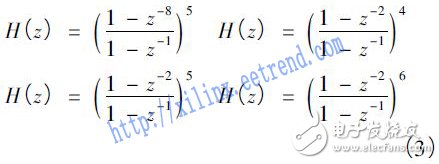
后三级CIC 滤波器的传输函数形式上是一样的,分成三级设计是为了将时钟频率逐级降低下来,尽可能地减少工作在高速时钟的逻辑,达到降低功耗的目的。
因为CIC 滤波器所占用的逻辑面积很小,选择Xilinx 公司的FPGA 芯片XC3S100E 来实现。它是Spartan3E 系列中逻辑门数少的芯片,已经足够实现CIC 功能和其它很多控制逻辑[11]。Sigma - Delta A/D 转换器输入数据在FPGA 内部经过四级CIC 滤波后产生8 kHz、24bit 数据。FPGA 通过SPI 接口将数据发送到MCU。
FIR 滤波器采用两级FIR 串联的形式达到滤波效果。由于CIC 滤波器在低频部分有着衰减的带宽,需要通过一个FIR 滤波器改善整个滤波系统低频部分的性能。其后另接一个FIR滤波器,产生一个快速下降的带宽,以对高频部分滤除。
FIR 滤波结构特点是没有反馈支路,即没有环路,其单位脉冲响应是有限长度。FIR 的特征函数将输入X( n) 和h( k) 做卷积运算,得到输出Y( n) 的差分方程为:
如图4 所示,FIR1 抽取滤波器为48 抽头( 47 阶) 4 抽取滤波器。FIR2 抽取滤波器为126 抽头( 127 阶) 2 抽取滤波器,Matlab 可以根据需要达到的滤波效果产生具体的滤波系数。
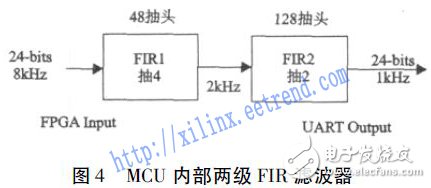
对于FIR 滤波器,从卷积公式可知,有K个系数的FIR 滤波对每个输入需要做K + 1 次乘法,在抽取时,这个运算可以被简化,不是每个输入都要跟每个系数相乘,可以只算有效的乘积,忽视会被抽取掉的选项,可以节约MCU资源,大大提高效率[12]。
抽取为M 时,则M 个数里有一个才是有效项,即式( 5) 所示:
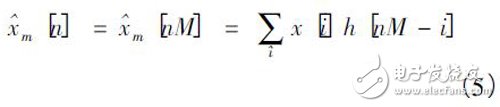
以一个阶数M 为3,抽样为3 的FIR 滤波器为例,它含有4 个系数,它的有效乘积项可以用图5 直观表示。

对一个有K 个系数,抽样为M 的FIR 来说,一般的算法除了开头的K - 1 个输入,以后每个输入都需要做K 次乘法运算; 优化后的算法每个输入只需要做[K /M]次乘法,其中[K /M]为系数个数除以抽样数后向上取整。
FIR 滤波部分由三部分组成: SPI 接口,FIR滤波器和串口。SPI 是MCU 跟FPGA 通讯的通道,MCU 从SPI 得到数据; FIR 滤波器为FIR 滤波功能实现模块; 串口为MCU 跟主机通讯的通道,主机可以通过串口给MCU 发指令,MCU 可以将处理完的数据用串口发给计算机。比如NXP 公司的LPC2106 芯片是一款ARM7 核的MCU,功耗低,数十兆赫兹的处理能力已经能够胜任32 kHz 的数据处理[13]。
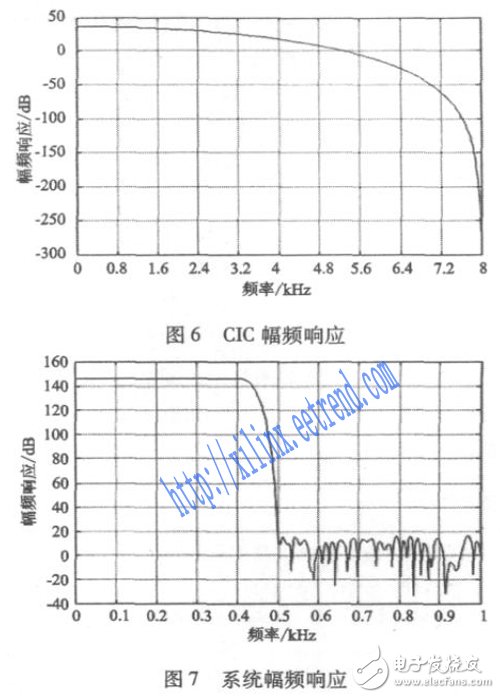
Matlab 可以对系统的性能做出理论上的分析。CIC 滤波器的幅频响应如图6 所示,可以看出CIC 在低频部分有着良好的响应,但是在高频部分下降得不够快。CIC 滤波器和FIR 滤波器的整体幅频响应如图7 所示,CIC 和FIR两级滤波器在430 Hz 以下有着良好的低通性能; 而在430 Hz ~ 500 Hz 的频率范围内,幅度响应下降了137 dB。
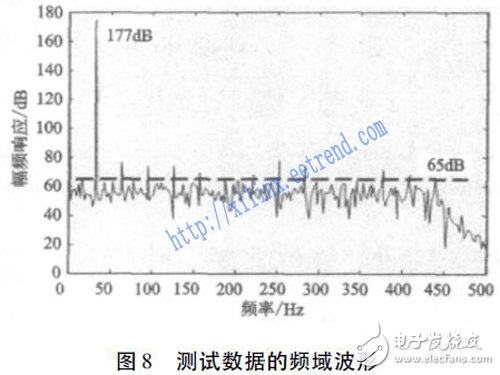
通过Matlab 仿真,可以从理论上得到CIC和FIR 构成的数字滤波器的性能。在实际中,可以通过真实的信号进行进一步的测试。在系统测试时,需要提供一个正弦波经过AD采样后的数据,这个电路可以通过CS4373和AD转换器CS5372 组成。CS4373 的主要功能是提供一个正弦信号,而CS5372 是高Sigma-Delta AD 转换器,能产生符合测试条件的串行bit 数据流,数据率为512 kb /s。
图8 是测试数据的频域波形,通过计算可以得到信噪好于110 dB,能够满足地震数据采集的需求。
本文针对地震数据采集系统中Sigma-Delta A/D 转换器后端的多级抽取滤波器进行了设计和实现。滤波器由四级CIC 滤波器和两级FIR滤波器构成,分别在FPGA 和MCU内实现。相对于专用的滤波芯片设计,极大地降低了成本。滤波器有着良好的低通性能,并能有效压制噪声,实测信噪比好于110 dB,能够很好地满足地震数据采集的需求。
这种FPGA 和MCU 相结合的方式所实现的地震信号滤波器,是一种低成本地震信号数字滤波器设计的尝试。从原理上验证了此类滤波器实现的可能性,并从性能上给出了初步的评估结果。但是这种方案的应用具有一定的局限性,它的功耗同商业滤波器相比相对较高。下一步可以在此方案的基础上进行实现方面的研究,从而达到性能、功耗和价格方面的多点平衡。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。