浅析Bang-Bang控制在随动系统中的应用

 

　　随动系统servo system,是一种反馈控制系统。在这种系统中，输出量是机械位移、速度或者加速度。因此随动系统这一术语，与位置或速度，或加速度控制系统是同义语。在随动系统中，有一类，它的参考输入不是时间的解析函数，如何变化事先并不知道（随着时间任意变化）。控制系统的任务是在各种情况下保证输出以一定跟随着参考输入的变化而变化。bang-bang控制在系统偏差大，可加大系统的控制力度，提高系统的快速性，因此，bang-bang控制是随动系统中不可缺少的控制方式。

　　bang-bang控制理论

　　bang-bang控制方面的研究始于20世纪50年代。在过去的20年中，鲁棒控制一直是国际自控界的研究热点。所谓"鲁棒性",是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。根据对性能的不同定义，可分为稳定鲁棒性和性能鲁棒性。以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。由于工作状况变动、外部干扰以及建模误差的缘故，实际工业过程的模型很难得到，而系统的各种故障也将导致模型的不确定性，因此可以说模型的不确定性在控制系统中广泛存在。

　　bang-bang控制早由庞特里亚金提出。在移动目标集的时间控制问题中，已知受控系统的状态方程为x（t）=f（x（t），t）+b（x（t），t）u（t），假设f（x（t），t）和b（x（t），t）的元对x（t）和t是连续可微的。r维容许控制向量u（t）的约束条件为|uj（t）|≤1,j=1,2,…，r.从初态x（t0）=x0出发，在某一末态时刻t>t0,首次达到移动目标集g（x（t），t）=0.其中g是p维向量函数，其各元对x（t）和t是连续可微的，同时性能指标j[u（。）]=∫dt t-t0为[6,7].控制u（f）应满足。

　　且=f（x（t），t）+b（x（t），t）u（t） （2）

　

    其中bj（x（t）,t）是矩阵b的第j列向量，则当达极小，于是bang-bang控制u（t）

　　即时间控制的各个分量u（t）都是时间t的分段常值函数，并在开关时间上由一个恒值到另一个恒值的跳变。

　　bang-bang控制在随动系统中的具体应用

　　现代鲁棒控制是一个着重控制算法可靠性研究的控制器设计方法。其设计目标是找到在实际环境中为保证安全要求控制系统必须满足的要求。一旦设计好这个控制器，它的参数不能改变而且控制性能能够保证。鲁棒控制方法，是对时间域或频率域来说，一般要假设过程动态特性的信息和它的变化范围。一些算法不需要的过程模型，但需要一些离线辨识。一般鲁棒控制系统的设计是以一些差的情况为基础，因此一般系统并不工作在状态。常用的设计方法有：INA方法，同时镇定，完整性控制器设计，鲁棒控制，鲁棒PID控制以及鲁棒极点配置，鲁棒观测器等。

　　在随动系统需要进行调转运动时，在某点需要以可能的加速度εm进行回归，此时误差|em|≥emax当到达某点时，又需要以-εm进行减速，当速度减到零时，误差也恰好为零，这就需要通过bang-bang控制来完成[2][3][4][5].如图1的bang-bang控制阈值曲线。

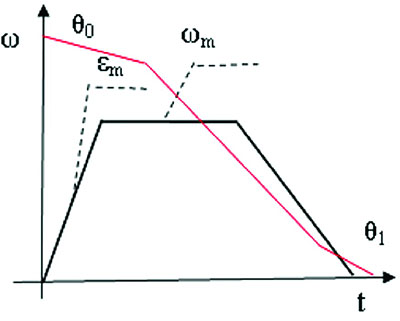
图1　bang-bang控制阈值曲线

　　图1中粗线表示速度变化曲线，细实线表示误差角变化曲线。当某一起点误差较大时，控制系统以可能的加速度εm进行加速，到达θ0点时以速度运行，当到达θ1点时以加速度-εm进行制动。当速度减到零时，其误差恰好等于零。这是理想的快的调转过程。要达到上述的要求就要正确判定转换点θ1,通常可以认为伺服电机的扭矩为恒定的，同时不考虑负载阻力矩的变化，系统可以看作为恒加速系统，则可以计算出开始制动时刻的误差角：

　　单片机收到电流反馈信号，经过bang-bang控制等智能协调处理得出输出控制量，根据输出量的大小确定pwm的占空比。主控制芯片选用intel公司的87c1961mc芯片，其自有的p1、p2、p3、p4口完满足控制需要。系统硬件简图如图2.

图2　系统硬件简图

　　软件实现

　　上面分析转换点和控制阈值都是理想的情况，实际上系统制动加速度εm的大小取决于电机的扭矩和负载的特性（阻力矩、转动惯量等参数）。控制程序内采用bang-bang算法设定的加速度大小应与负载实际加速度大小相对应，否则就会出现二次启动或超调过大现象，影响到系统性能。当控制程序内的制动加速度εm的值设定较小时，计算出来的制动角与实际的相比就会偏大，就会出现制动过早现象，即制动已经结束（速度已经降到零），但系统还没有到达预定位置，此时系统就会重新启动，这就是二次启动问题。这会造成调转时间过长，影响到系统的快速性。同时，当控制程序内的制动加速度εm的值设定较大时，计算出来的制动角与实际的相比就会偏小，就会出现制动过晚现象，即系统已经到达预定位置，但制动还没有结束（速度还没有降到零），此时系统出现超调。较小的超调是正常的，在负载上基本没有反映；超调很大时，机械负载就会有反映，即出现回摆现象，同时也会造成调转时间过长，影响到系统的快速性。出现二次启动或超调过大现象时，只需改动控制程序中的加速度参数即可解决。

　　系统进行调转控制程序流程图如图3.

图3　调转控制程序流程图

　　系统仿真

　　通过采样出的点，能绘出系统在进行不同阶跃运动时的曲线。同时，对系统进行仿真，能得出在正常制动、超调过大和二次启动的曲线，与采样出的曲线比较，相同运动状态下曲线基本吻合。具体仿真曲线如图4~6.

图4 二次启动简图　图5 回摆现象简图　图 6 正常制动简图

　　结语

　　仿真结果说明，bang-bang控制在随动系统调转控制能很好满足系统快速性的要求，达到阶跃过程化，并且结合其它控制方法能提高系统自适应能力和控制，有很好的推广价值。