一种二维混沌加密算法的设计和实现

 

　　随着计算机及通信技术的发展，图像处理及应用愈加广泛。现代DSP技术的发展和应用为实现图像处理奠定了基础。高性能的DSP处理器作为图像处理的器件，并能通过软件编程实现各种处理算法，提高系统处理能力和扩展系统功能。

　　近来混沌的同步控制理论日趋成熟，为混沌在通信中的应用提供了理论基础。混沌信号的非周期性连续宽带频谱，类似噪声的特性。另外，混沌信号对初始条件的高度敏感，即使两个完全相同的混沌系统从近乎相同的初始条件开始演化，其轨道将很快变得互不相关，这使得混沌信号具有长期不可预测性和抗截获能力。而且具有多个正李氏指数的超混沌系统，及复杂的运动轨迹，这使得混沌信号具有较高的复杂度。同时混沌系统本身具有确定性，由非线性系统的方程、参数和初始条件所决定，因此，混沌信号易于产生复制。混沌信号的隐蔽性、不可预测性、高复杂度和易于实现等特性都适合于保密通信。与其他加密方法不同的是，混沌加密是一种动态加密方法，由于其处理速度和密钥长度无关，因此这种方法的计算效率高、可用于实时信号处理和静态加密场合。且用此方法加密的信息很难破译，具有很高的保密度。即使在连续摄动存在的情况下，混沌同步效应过程也是稳定的。特别是在混沌信号上加上一个较小的信息源，当混合信号传到接收器上后，由接收器上参数相同的混沌电路捕捉其中主要的混沌分量，可以较好地恢复输送的信息源。

 

　　1 混沌系统

　　1.1  一维Logistic序列[4]的混沌特性

    混沌现象是在确定性非线性动力系统中出现的确定性、类随机的过程，这种过程没有明显的周期和对称，但是却具有丰富的内部层次的有序结构，并且对初始值有极其敏感的依赖性。Logistic映射是一种常见的混沌动力系统，基于一维Logistic映射进行加密是一种平凡的混沌加密，安全性难以保障，但可以证明二维Logistic映射所产生的混沌点集合不存在误差构造形式，具有更安全的加密效果。

    Logistic映射是目前被广泛应用的一种混沌动力系统，其表达式为：

 

 

　　1.2  二维Logistic序列的混沌特性和统计特性

    二维Logistic映射的系统模型为：

 

 

　　1.3 加密模板

    本文采用的加密模块为：

 

 

　　2 小波变换

    采用双正交9／7小波[5]作图像的二级小波分解，获得7个子带，从低到高分别为LL2，HL2，LH2，HH2，HL1，LH1和HH1。图像子带特性有以下情况：LL2子带的能量大约占图像信号总能量的95%；第2层(LL2、HL2、LH2、HH2、HL1)子带的能量大约占图像信号总能量的97．5%；除LL2中的值基本是正值以外，其余各子带的值有正有负。本文算法根据变换域的图像能量的特点对LL2层系数进行位扩展的混沌置乱。二级小波的分解如图1所示。

 

 

　　3 加密/解密系统

　　3.1 加密过程

　　加密过程如图2所示。

 

 

　　3.2 加密步骤

    输入：原始图像、参数1、参数2、参数3、参数4、……。

    输出：加密图像。

    加密步聚如下：

    (1) 首先对大小为N×N的lena图像进行连续小波变换，本文采用的是二级bior3．7小波分解。

    (2) 根据输入的混沌参数由一维混沌映射开始迭代产生混沌序列，根据式(3)产生加密模板，并根据加密模板对二级小波分解后的各个系数进行调整。

    (3) 将调整后的小波系数分成低频部分(LL2)和高频部分(包括水平区域(HL2，HL1)、垂直区域(LH2，LH1)和对角线组(HH2，HH1)3个部分)，选择低频系数进行位扩展[6]加密， 根据输入的混沌参数由二维混沌序列生成序列x(n)和y(n)，其中x(n)序列用来对低频部分进行位扩展加密，将x(n)从中间某位截断取大小为1/4×N×N个数，以0.5为阈值对x(n)进行二值化，得到一个1/4×N×N大小的二值序列S,将二值序列S中的第8×j位到8×j+7位的8个二进制位组成数据t(j),将t(j)与调整系数后的低频部分进行“异或”处理，即得到位扩展加密后的低频部分系数。

    (4) 对置乱后的小波低频系数和未进行处理的高频系数共同进行小波逆变换得到图像I，同时用二维混沌映射产生的大小为N×N的序列y(n)对图像I进行置乱加密，得到的加密图像。

　　3.3 解密步骤

　　输入大小为N×N的待解密图像，二维混沌映射参数得到序列y（n）与待解密图像行进行"异或"处理，得到的图像进行二级bior3.7小波分解。将得到的小波系数的低频系数进行位扩展运算，将解密后的系数与其他的高频系数与混沌模板解密矩阵点乘，得到的小波系数。对小波系数进行小波逆变换，得到解密后的图像。

　　4 实验结果及分析

　　4.1 破解实验

 

 

　　4.2 耗时测试

    耗时测试实验目的是验证位扩展混沌算法的时效性。Arnold算法在图像尺寸为128×128、256×256、512×512的周期依次为96，192，384，分别设定密钥为50、100、200；位扩展算法的密钥设为a=1.952，x0=0.143,则结果如表1所示。

 

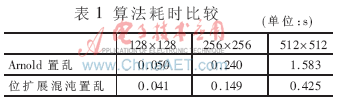
　　由表1可知，基于为扩展的混沌算法在实效上优于Arnold算法，图像越大优势越明显。

　　4.3 压缩分析

　　在基于小波压缩域的加密技术中，目前主要两种方法为CWW和CWF.CWW指在整个图像N×N的范围内置乱，使得高频系数和低频系数产生迁移。若要进行编码或压缩处理时，低频到高频的系数迁移会造成量化误差，影响解码的质量，甚至会造成比特溢出而无法继续编码过程；而高频到低频的迁移，则会严重影响编码的效率。这种对整个小波系数的置乱方法对压缩的能力影响极大，会使得有损压缩无法进行。因此本文只在同一个频带内置乱则不会出现这种情况，使得本算法适合于压缩编码等情况。压缩处理过程只会造成解密图像质量的下降，不会对图像要表达的内容构成实质性损害。

　　本文将位扩展运算运用于小波域来加密图像，同时与混沌模板序列相结合，并利用二维混沌序列对图像的小波系数进行置乱和置换变换，实现了小波变换域的高强度加密。本文提出的算法不仅能获得很好的加密效果，而且相比于其他的置乱算法，可以很大程度地节约计算时间，减小计算的复杂度。同时采用混沌加密模板，比传统的混沌序列有更高的加密强度。密钥简单，但空间却很大，不易破解。仿真实验表明，该算法的实用性很强，在不改变小波系数值的前提下，运算速度快，加密造成的膨胀量小。