分析基于DSP自适应滤波算法的仿真及工程实现

　　自适应滤波理论是20世纪50年代末开始发展起来的。它是现代信号处理技术的重要组成部分，对复杂信号的处理具有独特的功能。自适应滤波器是仅需对当前观察的数据作处理的滤波算法。它能自动调节本身冲激下响应的特性，或者说自动调节数字滤波器的系数，以适应信号变化的特性，从而达到滤波。自适应滤波器主要由两部分组成：系数可调的数字滤波器和用来调节或修正滤波器的系数的自适应算法。由于自适应滤波不需要关于信号的先验知识，具有计算量小的特点，特别适合于实时处理，近年来得到广泛的应用，例如：脑电图和心电图的测量、噪声抵消、扩频通信及数字电话等。

　　在一些信号和噪声特性无法预知或它们是随时间变化的情况下，自适应滤波器通过自适应滤波算法调整滤波器系数，使得滤波器的特性随信号和噪声的变化而变化，以达到滤波的效果。本文在对自适应滤波算法研究的基础上，给出了不同信噪比情况下，LMS算法的仿真实现及基于DSP的工程实现，并对两种实现方法的结果进行了验证、分析比较。

　　1 自适应滤波理论

　　所谓自适应滤波，就是利用前一时刻已获得的滤波器参数等结果，自动调节现时刻的滤波器参数，以适应信号和噪声未知或随时间变化的统计特性，从而实现滤波。自适应滤波器的特点是自动调节自身的冲激响应，达到滤波，此算法适用于平稳和非平稳随机信号，并且不要求知道信号和噪声的统计特性。

　　1.1 自适应滤波器结构

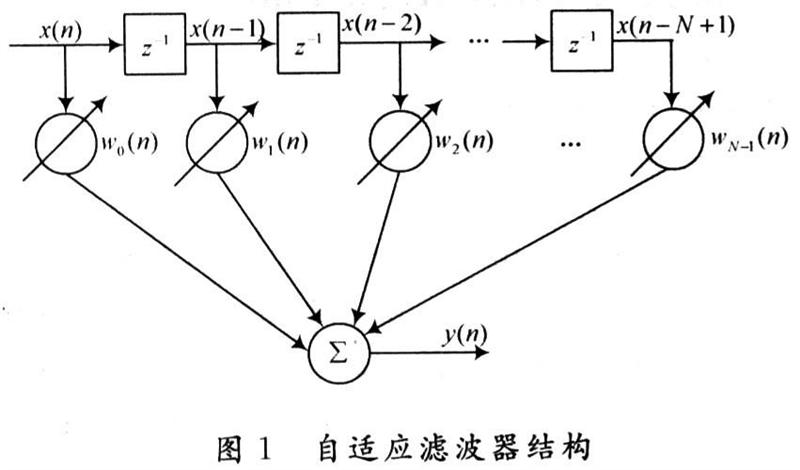
　　自适应滤波器主要有无限冲激响应（IIR）和有限冲激响应（FIR）两种类型。滤波器结构的选择对算法的处理起着重要的影响；IIR型结构滤波器的传输函数既有零点又有极点，它可以用不高的阶数实现具有陡峭通带特性，缺点是稳定性不好，且相位特性难于控制。FIR滤波器是全零点滤波器，它是稳定的，且能实现线性的相位特性，因此，自适应滤波器的结构通常采用F1R型滤波器的横向结构，结构如图1所示。

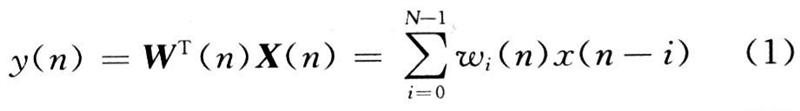
　　式中：n为时间序列；N为滤波器阶数；x（n）=[x（n），x（n-1），…，x（n-N+1）]T为输入矢量；W（n）=[ω0（n），ω1（n），…，ωN-1（n）]T为权系数矢量。

　　1.2 LMS自适应滤波算法

　　LMS 自适应算法即均方误差自适应算法。算法思想为：假设给出了和原始信号相关的参数信号d（n），那么首先对FIR 滤波器的权任意设定一组初始值，然后根据滤波器的输出值与参考信号之间的误差e（n）对权值进行调节，使下的输出误差能有所减小，这样重复下去，直到权收敛到值。误差序列的均方值ε表示为：

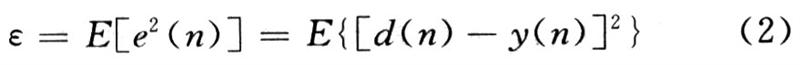
　　式中：d（n）为理想信号；e（n）为输出误差序列。将式（1）中的y（n）代人式（2）中有：

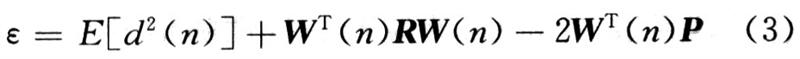
　　式中：R=E[X（n）XT（n）]为N×N自相关矩阵，表示输入信号采样值间的相关性矩阵。P=E[d（n）X（n）]为N×1互相关矩阵，表示理想信号d（n）与输入信号矢量的相关性。

　　在均方误差时，权系数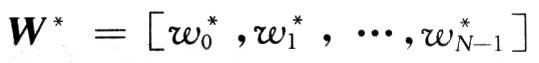应满足如下方程：

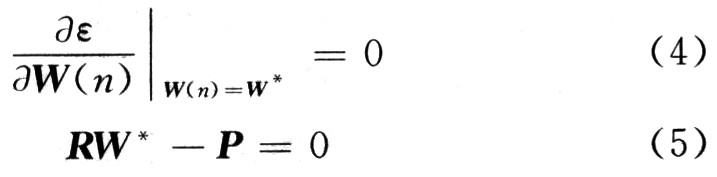
　　即：这是一个线性方程组，如果R矩阵为满秩矩阵，则有R-1存在，可得到权系数的值满足：

　　由式（6）可以知道，求出R和P就可以得到W*。由前几式可知，R是X（n）的自相关矩阵，P是d（n）与 X（n）的互相关矢量。

　　LMS算法是以陡下降法为原则的迭代算法，即W（n+1）矢量是W（n）矢量按均方误差性能平面的复斜率大小调节响应一个增量，即：

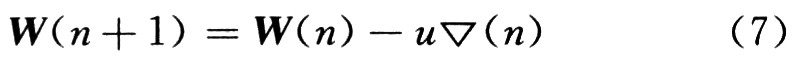
　　式中：u表示自适应步长；（n）为n次迭代的梯度，表示为：

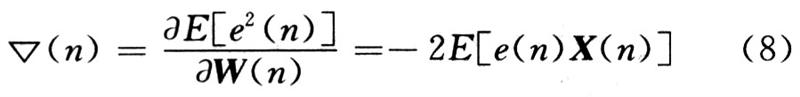
　　由式（7）产生了求解权系数W*方法的两种方法，一种是陡梯度法，其基本思路为：设定初始权系数W（0），用式（7）迭代公式计算，迭代直到W（n+1）与 W（n）误差小于规定范围。其中（n）的E[]计算可用下面的估计值表达式来计算：

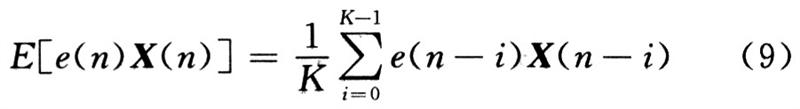
　　式中K取值应足够大。如果用瞬时-2e（n）X（n）来代替上面对-2E[e（n）X（n）]的估计运算，就产生另一种算法：随机梯度法，即Widrow-Hoff的LMS算法。迭代公式表示为：

　　2 仿真及工程实现

　　2.1 LMS算法的仿真实现

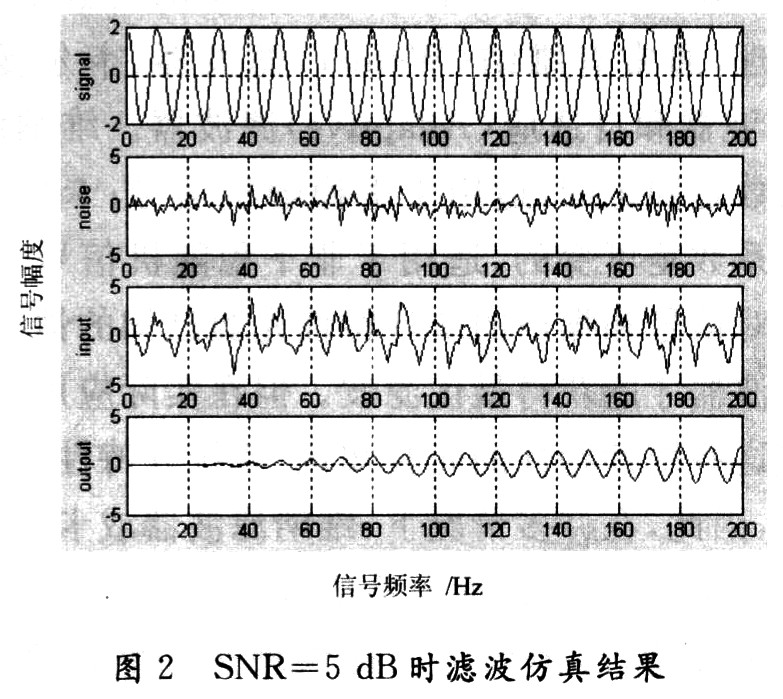
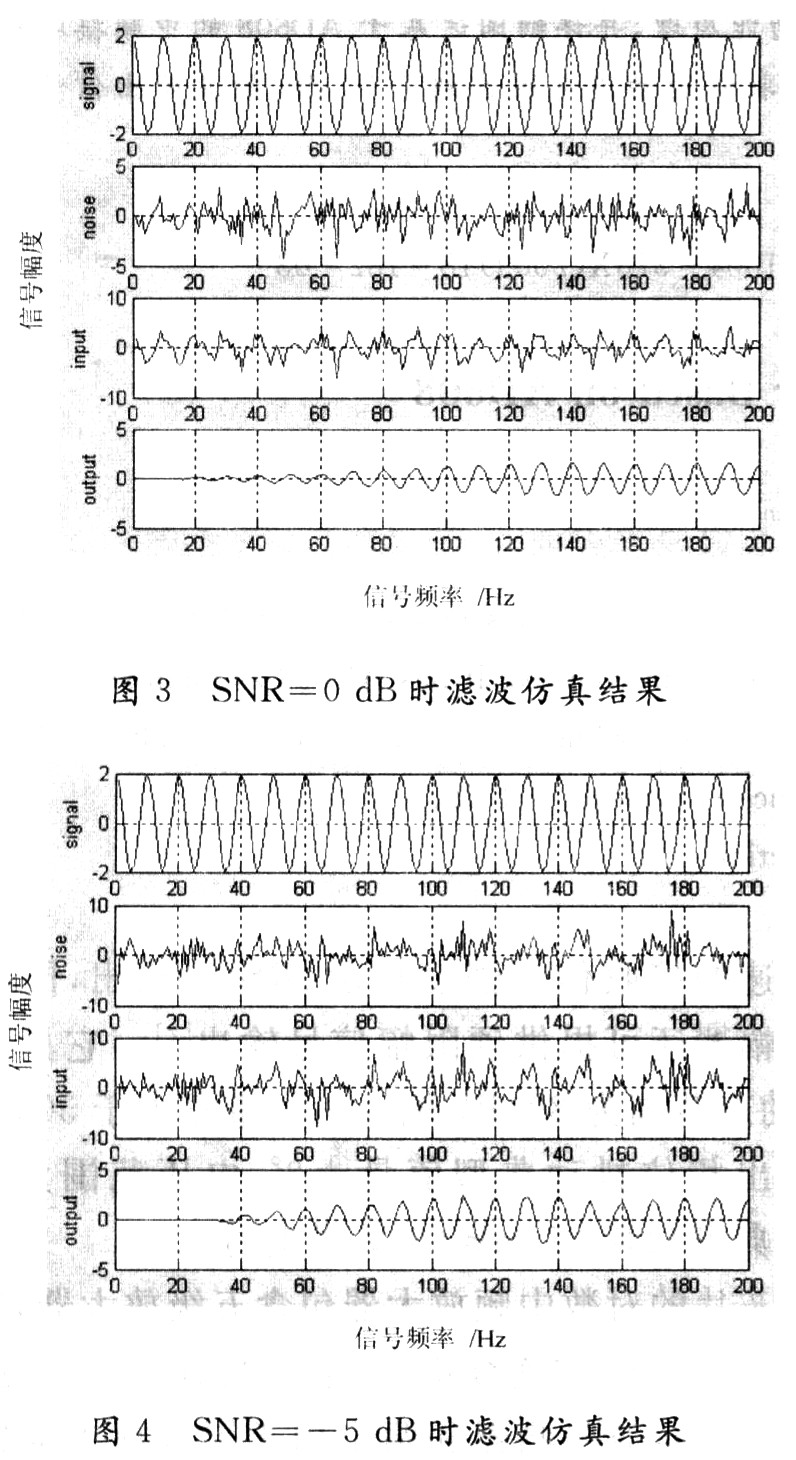
　　假定输入信号由正弦波信号和高斯白噪声组成。其中正弦波信号的频率f0=1 000 Hz，幅度A=2，FIR滤波器的阶数N为128；当白噪声的均值为0，其方差δ分别为0.64，2，6.32，即信噪比（SNR）分别为5 dB，0 dB，-5 dB时，采用LMS算法进行滤波的结果分别如图2～图4所示。

　　2.2 LMS算法的DSP实现

　　设定采样数据的点数为1024点，滤波器的全系数设定为128阶，自适应步长为5×10-5。设定输入信号为正弦波+噪声信号，其中正弦波的周期T=256 s，幅度A=200，正弦波信号功率Ps=20 000；噪声设定为零均值，方差δ分别为2 000，6 330，20 000，相应的信噪比 SNR=10 dB，5 dB，0 dB，根据自适应迭代公式（8），使用DSP编程实现自适应滤波算法，由DSP的CCS开发环境图形分析工具得到测试结果如图5～图7所示。

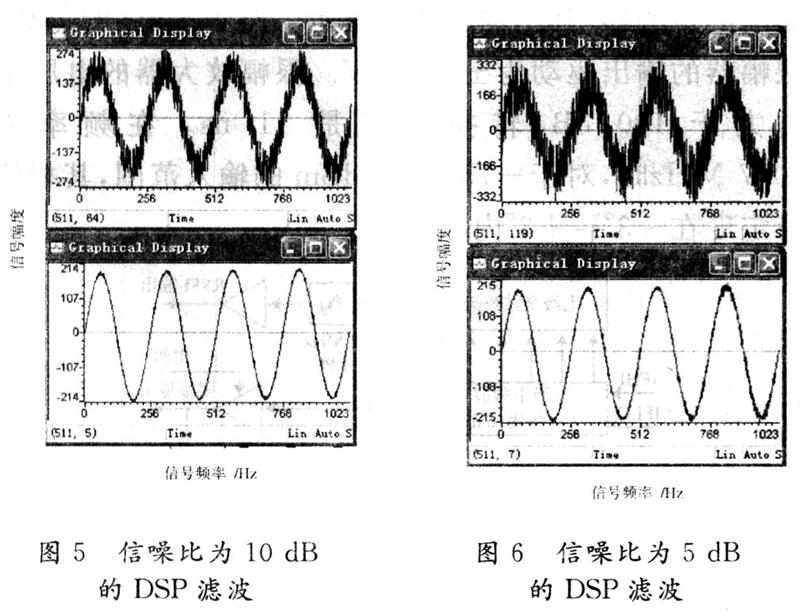
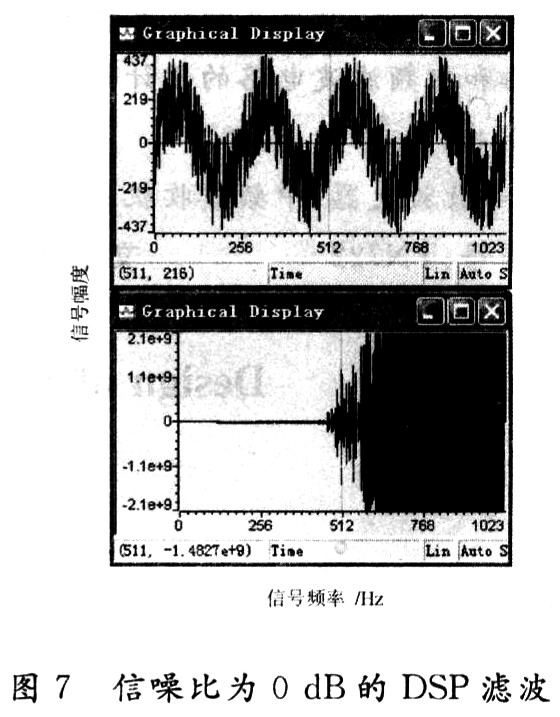
　　根据图7比较分析可以得出：

　　（1）无论是使用Matlab仿真方法还是使用DSP方法实现LMS算法，随着信噪比的降低，自适应滤波效果减弱。

　　（2）在信噪比位于0 dB之上时，两种方法都可以取得较好的滤波效果。

　　（3）在信噪比位于0 dB（或0 dB以下），仿真方法可以取得较好的滤波效果，但工程上却不能实现，即当信噪比位于0 dB时，LMS算法已失去工程上的应用价值。

　　3 结 语

　　本文在对自适应滤波理论研究的基础上，对LMS自适应滤波算法进行了研究，给出了不同信噪比条件下，LMS算法的仿真实现及基于DSP的工程实现，并对两种实现结果进行了分析比较，通过如图7所示，LMS算法在信噪比较高时，除噪效果非常显着，当信噪比较低的时候，仿真上可以得到的比较理想的滤波效果，工程上却无法实现。该结论对于指导自适应滤波理论的工程实践具有指导作用。