基于DSP自适应滤波器的算法研究及实现

 

　　随着DSP技术的高建发展，人们对信号处理的实时性、准确性和灵活性的要求越来越高，DSP技术在信号处理中的地位也越来越重要。自适应滤波器是一种复杂的算法，设计它是为了在均衡信道，抵消回波，增强谱线，抑制噪声等方面有所应用。而自适应滤波器的实现主要采用均方误差算法完成。自适应算法通过调整滤波器系数来实现可以更好地跟踪信号的变化，终实现自适应滤波。

　　滤波是电子信息处理领域的一种基本而又极其重要的技术。在有用信号的传输过程中，通常会受到噪声或干扰的污染。利用滤波技术可以从复杂的信号中提取所需要的信号，同时抑制噪声或干扰信号，以便更有效地利用原始信号。滤波器实际上是一种选频系统，它对某些频率的信号予以很小的衰减，让该部分信号顺利通过；而对其他不需要的频率信号则予以很大的衰减，尽可能阻止这些信号通过。在电子系统中滤波器是一种基本的单元电路，使用很多，技术也较为复杂，有时滤波器的优劣直接决定产品的性能，所以很多国家非常重视滤波器的理论研究和产品开发。

　　1 自适应滤波器简介

　　自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器。作为对比，非自适应滤波器有静态的滤波器系数，这些静态系数一起组成传递函数。对于一些应用来说，由于事先并不知道所需要进行操作的参数，例如一些噪声信号的特性，所以要求使用自适应的系数进行处理。在这种情况下，通常使用自适应滤波器，自适应滤波器使用反馈来调整滤波器系数以及频率响应。总的来说，自适应的过程涉及到将价值函数用于确定如何更改滤波器系数从而减小下迭代过程成本的算法。价值函数是滤波器性能的判断准则，比如减小输入信号中的噪声成分的能力。随着数字信号处理器性能的增强，自适应滤波器的应用越来越常见，时至今日它们已经广泛地用于手机以及其它通信设备、数码录像机和数码照相机以及医疗监测设备中。

　　2 自适应滤波原理

　　自适应滤波器主要有无限冲激响应（IIR）和有限冲激响应（FIR）两种类型，滤波器结构的选择对算法的处理起着重要的影响。IIR型结构滤波器的传输函数既有零点又有极点，他可以用不高的阶数实现具有陡峭通带特性，缺点是稳定性不好，且相位特性难于控制。FIR滤波器是全零点滤波器，他是稳定的，且能实现线性的相位特性[2]，因此，自适应滤波器的结构通常采用FIR型滤波器的横向结构。

　　自适应滤波器的特性变化是由自适应算法通过调整滤波器系数来实现的。一般而言，自适应滤波器由两部分组成，一是滤波器结构，二是调整滤波器系数的自适应算法。自适应滤波器的结构采用FIR或IIR结构均可，由于IIR滤波器存在稳定性问题，因此一般采用FIR滤波器作为自适应滤波器的结构。图1给出了自适应滤波器的一般结构。

 

 

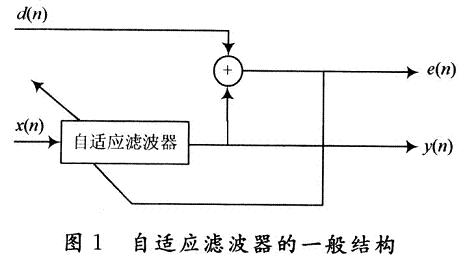
　　图1为自适应滤波器结构的一般形式，图中x(n)为输入信号，通过参数可调的数字滤波器后产生输出信号y(n)，将输出信号y(n)与标准信号(或者为期望信号)d(n)进行比较，得到误差信号e(n)。e(n)和x(n)通过自适应算法对滤波器的参数进行调整，调整的目的使得误差信号e(n)。

　　自适应滤波器设计中常用的是FIR横向型结构。图2是横向型滤波器的结构示意图。

 

 

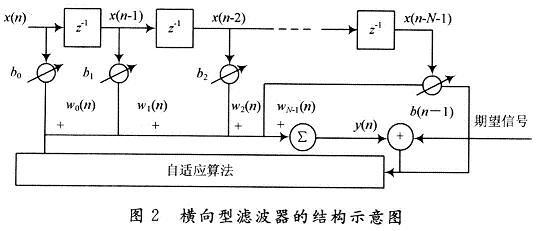
　　其中：x(n)为自适应滤波器的输入；w(n)为自适应滤波器的冲激响应：w(n)={w(O)，w(1)，…，w(N-1)}；y(n)为自适应

 

 

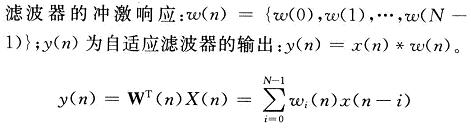
　　3 自适应滤波算法

　　自适应滤波器除了包括一个按照某种结构设计的滤波器，还有一套自适应的算法。自适应算法是根据某种判断来设计的。自适应滤波器的算法主要是以各种判据条件作为推算基础的。通常有两种判据条件：均方误差判据和二乘法判据。LMS算法是以均方误差为判据的典型的算法，也是应用广泛的一种算法。

　　均方误差(Least Mean Square，LMS)算法是一种易于实现、性能稳健、应用广泛的算法。所有的滤波器系数调整算法都是设法使y(n)接近d(n)，所不同的只是对于这种接近的评价标准不同。LMS算法的目标是通过调整系数，使输出误差序列e(n)=d(n)-y(n)的均方值化，并且根据这个判据来修改权系数，该算法因此而得名。误差序列的均方值又叫“均方误差”(Mean Sqluare Error，MSE)。

　　理想信号d(n)与滤波器输出y(n)之差e(n)的期望值，并且根据这个判据来修改权系数wi(n)。由此产生的算法称为LMS。均方误差ε表示为：

 

 

　　对于横向结构的滤波器，代入y(n)的表达式：

 

 

　　其中：R=E[X(n)XT(n)]为N×N的自相关矩阵，它是输入信号采样值间的相关性矩阵。P=E[d(n)X(n)]为N×1互相关矢量，代表理想信号d(n)与输入矢量的相关性。在均方误差ε达到时，得到权系数

它应满足下式：

　　这是一个线形方程组，如果R矩阵为满秩的，R-1存在，可得到权系数的值满足：W*=R-1p。用完整的矩阵表示为：

　　显然φx(m)=E[x(n)x(n-m)]为x(n)的自相关值，φxd(R)=E[x(n)d(n一k)]为x(n)与d(n)互相关值。在有些应用中，把输入信号的采样值分成相同的一段(每段称为一帧)，再求出R，P的估计值得到每帧的权系数。这种方法称为块对块自适应算法。如语音信号的线性预测编码LPC就是把语音信号分成帧进行处理的。R，P的计算，要求出期望值E，在现实运算中不容易实现，为此可通过下式进行估计：

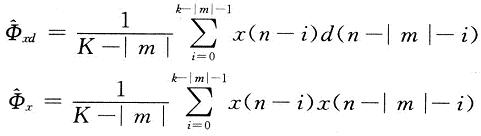
　　用以上方法获得W*的运算量很大，对于一些在线或实时应用的场合，无法满足其时间要求。大多数场合使用迭代算法，对每次采样值就求出较佳权系数，称为采样值对采样值迭代算法。迭代算法可以避免复杂的R-1和P的运算，又能实时求得近似解，因而切实可行。LMS算法是以快下降法为原则的迭代算法，即W(n+1)矢量是W(n)矢量按均方误差性能平面的负斜率大小调节相应一个增量：W(n+1)=W(n)-μ▽(n)，这个“是由系统稳定性和迭代运算收敛速度决定的自适应步长。▽(n)为n次迭代的梯度。对于LMS算法▽(n)为下式E[e2(n)]的斜率：

 

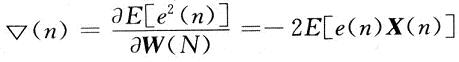
　　由上式产生了求解权系数W*的两种方法，一种是陡梯度法。其思路为：设计初始权系数W(0)，用W(n+1)=W(n)一μ▽(n)迭代公式计算，到W(n+1)与W(n)误差小于规定范围。其中▽(n)计算可用估计值表达式：

 

 

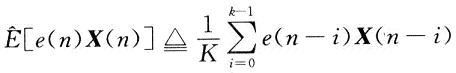
　　上式K取值应足够大。如果用瞬时一2e（n）X（n）来代替上面对-2E[e（n）X（n）]的估计运算，就产生了另一种算法——随机梯度法，即Widrow-Hoft的LMS算法。此时迭代公式为：

　　W（n+1）=W（n）+2ue（n）X（n）

　　以后讨论的LMS算法都是基于WidrOW-Hoff的LMS算法。上式的迭代公式假定滤波器结构为横向结构。对于对称横向型结构也可推出类似的迭代公式：

　　W（n+1）=W（n）+2ue（n）[X（n）+X（n一N+1）]

 

　　4 自适应滤波算法的理论仿真

　　使用Matlab编程，采用自适应滤波器技术实现信噪分离，也就是去噪。程序如下：

　　程序运行的结果如图3所示。

 

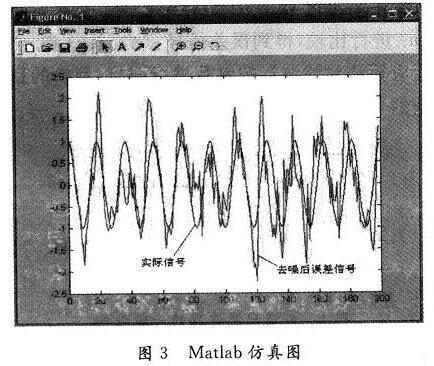
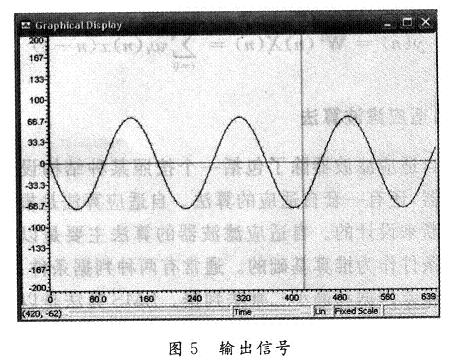
　　通过CCS软件环境，把滤波程序烧录到DSP芯片中，在CCS DSK C5000环境下输出仿真结果：输入信号为余弦信号和随机噪声的叠加。程序正确运行后，观察运行结果，得出如图4，图5所示的仿真图。

 

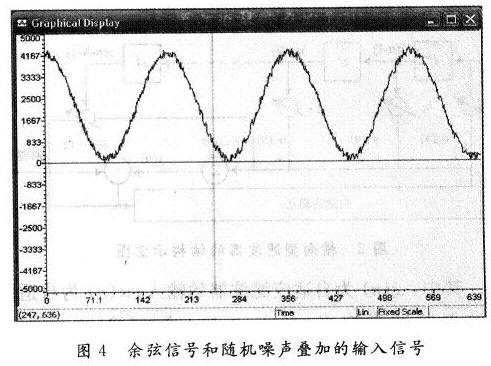
　　5 结 语

　　本文对自适应滤波器理论进行了系统的阐述和分析，并在已知理论的基础上对LMS自适应滤波器算法进行了仿真研究，仿真结果表明：自适应滤波算法在信噪比比较大的时候，除噪效果非常显着，即使在信噪比较小时，只要选择合适的步长参数u和合适的滤波器阶数就可以得到比较理想的结果。更为重要的是该算法运算量小、易于工程实现，这些优点使自适应滤波算法成为应用广泛的一种自适应滤波算法。