单片机浮点数的实用快速除法介绍

　　作为单片机程序员来说，在编写程序时经常要检验程序中的浮点数运算结果是否正确，但手中又没有合适的检验工具，非常麻烦。而一般单片机是没有浮点数运算指令的，必须自行编制相应软件。在进行除法计算时，通常使用的方法是比较除法，即利用循环移位和减法操作来得到24～32位商，效率很低。这里给出一种浮点数除法运算的实用快速算法。该方法以数值计算中的预估-修正方法为指导，充分利用了16位单片机的乘除法功能，很轻易地实现了浮点数的除法。

　　1 浮点数格式

　　IEEE的浮点数标准规定了单（4字节）、双（8字节）和扩展（10字节）三种浮点数的格式。常用的是单浮点数，格式如图1所示。但是这种格式的阶码不在同一个字节单元内，不易寻址，从而会影响运算速度。

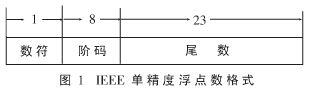
　　通常在单片机上采用的是一种变形格式的浮点数，如图2所示。其中的23位尾数加上隐含的位1，构成一个定点原码小数，即尾数为小于1大于等于0.5的小数。

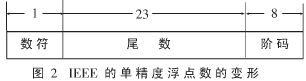
　　2 快速除法的算法原理

　　在16位单片机中只有16位的乘除法，而浮点数的（即尾数的有效位数）达24位，因此无法直接相除，但依然可以利用16位的乘除法指令来实现24位除法。不过，如果只进行16位的除法必定会带来很大误差，因此问题的关键在于如何消除这个误差，从而达到要求的。这其实就是通常数值计算中所采用的预估-修正方法。

　　假设两个浮点数经过预处理后，被除数和除数尾数扩展为32位（末8位为0）分别放入X和Y中。邻YL为Y的低16位，并记YH=Y-YL。显然YH≈Y，X/Y与Y/YH相差不多：

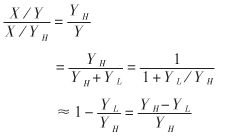
　　可见只需要在X/YH的基础上再乘以一个修正因子（YH-YL）/YH，就可以得到X/Y的校准值。不难证明这个值已经达到了24位的要求。事实上，相对误差满足：

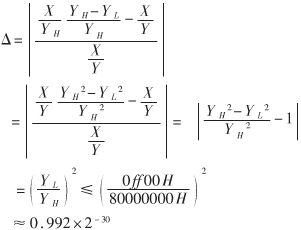
　　这说明这个校准值完全可以作为终的结果。

　　3 算法的具体实现

　　在具体实现本算法时，主要经过下列步骤：

   

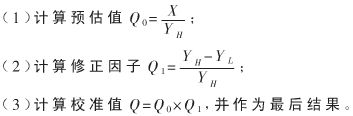
　　这里的YH虽仍是32位，但其低16位已为0，计算时可以将它视为16位数，这不会影响计算。通过两次16位除法，就可得到的32位结果。例如，计算Q0时，次除法，X除以YH的高16位，得到的商为Q0的高16位，而16位余数末尾添0成32位，再除以YH的高16位，得到Q0的低16位（余数舍去）。由此得到了32位的Q0。

　　在具体运算中，X应选除以4（X左移2位），以保证Q0不会溢出（YH取高16位）：

　　

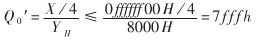
　　由于X为32位（末8位为0），这一操作不影响有效数字。而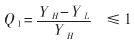，不存在溢出的问题。计算校准值Q时，有。

　　在计算Q0'、Q1时，均进行了两次16位除法，使得Q0'、Q1均为的32位，保证了计算过程中的，减小了累积误差。对于YL=0即除数只有16位有效数字的特殊情况，直接有Q1=1，还能省去两次16位除法。

　　在计算Q时，则通过3次16位乘法实现了32位乘法，取结果的高32位，即得Q。

　　整个算法至多只须用4次除法、3次乘法和5次加法，就求得了浮点数商的尾数，可见计算效率是很高的，保证了运算速度。

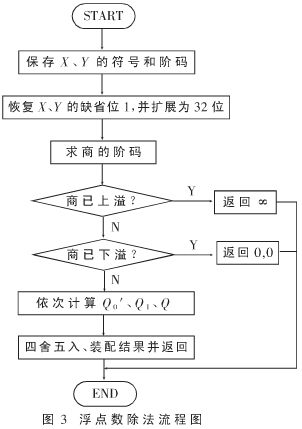
　　浮点数除法流程图如图3所示。

　　4 程序源代码

　　限于篇幅，只给出源代码中的关键部分，即有效数字的计算部分。

  

　　代码到这里为止，浮点数商的有效数字已经全部求出。只要再执行一些调整浮点数阶码的操作，就可以得到终结果。

　　在作者开发的一个80C196KC单片机系统中，涉及到了二进制-十进制数制转换、分段线性插值、数字滤波等大量浮点数的运算，都是靠加减乘除等底层函数来实现的。

　　此外，本算法思路清晰，因此很容易加以推广。例如，为了得到更高的，可取修正因子：

   

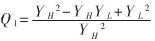
　　则相对误差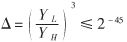，转化为十进制，有效数字高达14位。