分形图像压缩及应用

　　摘要：近10年来 ,基于分形的图像压缩技术发展很快。分形图像压缩技术具有极高的压缩比、快速的解压缩速度 ,在图像通信、多媒体、互联网中得到了广泛的应用。分形几何理论研究的是很不规则的如粗糙、不光滑、破碎、扭曲、缠绕等且有自相似性的形状。分形具有精细的结构 ,有任意小比例的细节 ,其局部和整体都不能用传统的几何语言来描述 ,通常有某种自相似的形式 ,其“分形维数 "一般大于其拓扑维数 ,能以非常简单的方法定义 ,由迭代方法产生。

　　1 分形的概念

　　分形，是以非整数维形式充填空间的形态特征。分形可以说是来自于一种思维上的理论存在。1973年，曼德勃罗（B.B.Mandelbrot）在法兰西学院讲课时，首次提出了分维和分形几何的设想。分形（Fractal）一词，是曼德勃罗创造出来的，其原意具有不规则、支离破碎等意义，分形几何学是一门以非规则几何形态为研究对象的几何学。由于不规则现象在自然界是普遍存在的，因此分形几何又称为描述大自然的几何学。分形几何建立以后，很快就引起了许多学科的关注，这是由于它不仅在理论上，而且在实用上都具有重要价值。

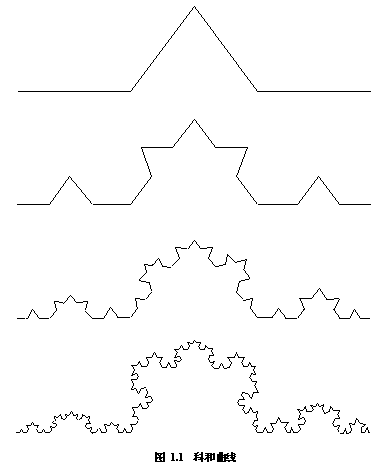
　　看看由瑞典数学家科和在1904年设计的一段曲线：在单位长度的直线段E0中间，以边长为1/3 E0的等边三角形的两边去代替E0中间的1/3，得到E1（见图1.1）。对E1的每条线段重复上述做法又得到E2，对E2的每段又重复，如此下去得到的极限曲线就是科和曲线。显然，科和曲线处处是尖点，因而处处没有切线；它的长度也不难证明是无穷的，因而传统的几何方法对科和曲线很难处理。

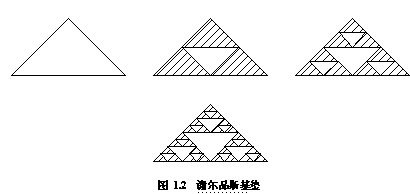
　　波兰数学家谢尔品斯基从平面二维图形出发，用重复某一过程的办法形成的曲线也是分形曲线的典型例子。如谢尔品斯基垫，它以一个三角形作为源图形，以源三角形的1/4大小的倒三角形作为生成元。不断重复上述步骤得到的极限曲线就称为谢尔品斯基垫（见图1.2）。

　　分形理论和应用发展很快，但至今还没有关于什么是分形的统一定义。一般公认法尔科纳对分形定义的描述比较合理：

　　分形应有精细的结构，有任意小比例的细节；

　　它是如此的不规则，以至其局部和整体都不能用传统的几何语言来描述；

　　分行通常有某种自相似的形式，可能是近似的或是统计的；

　　其“分形维数"一般大于其拓扑维数；

　　分形通常能以非常简单的方法定义，由迭代方法产生。

　　从科和曲线或谢尔品斯基垫的例子中不难看到以上特点，但“分形维数”值得一提。“分形维数”是一个表征分形复杂或粗糙程度的量，在欧氏几何中，维数总是取整数，直线是一维，平面是二维，立体是三维。推广过程如下。在图1.3中，以尺寸为ε的量尺测量大小为L的物体，量得的个数记为N，

　　则有N = （ L/ε）d

　　其中d就是维数，从图中可以看出，d分别为1，2，3。也可以认为：

　　d = lnN / ln（L/ε）

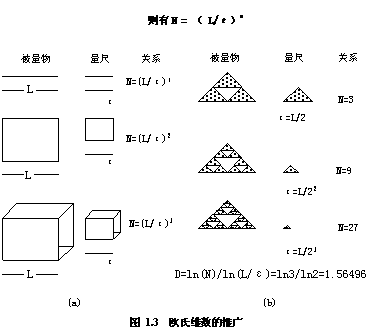
　　把这种方法推广到谢尔品斯基垫上，不难得到它的维数d为：

　　d = ln3 / ln2 = 1.58496

　　用类似的方法可以求得科和曲线的维数d = ln4 / ln3。需要指出，这种维数称为相似维数，它适用于有严格自相似的分形集合。

　　建立了分形维数的概念，就可以理解为什么用传统的几何方法去度量不列颠海岸线或者科和曲线的长度时，得不到准确结果。对待这些曲线，要先计算其分形维数，只有在相同维数下度量才有意义。

　　2 分形图象压缩

　　2.1 收缩仿射变换（Contractive Affine Transformation）

 

　　如果1个平面图形上的各点经过线性变换

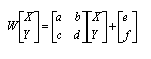
    后，图形上各点的距离比原有的距离要小，那么就称这种变换是收缩仿射变换。这个变换的a，b，…，f是变换矩阵的系数。比如，一个变换为：

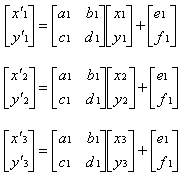
　　用它对图2.1（a）的图F各点进行变换，变换后得到W（F）（见图2.1（b））。其形状与原图形F相似，但各点的距离缩短。显然，如果对一个图形反复施加收缩仿射变换，即对W（F）再行变换得到W2（F），对W2（F）又施行变换得到W3（F）……，其迭代的结果将使原来图形收缩为一个点。

　　收缩仿射变换原理：在有限维的情况，每个仿射变换可以由一个矩阵A和一个向量双仿射变换b给出，它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了右边是一个1，而列向量的底下要加上一个1。

　　AffineTransform类描述了一种二维仿射变换的功能，它是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直性”（译注： straightness，即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（译注：parallelness，其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变。大二学过的复变，“保形变换/保角变换”都还记得吧，数学就是王道啊！）。仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和错切（Shear）。

　　2.2 迭代函数系统（Iterated Function System）

　　人们把若干个收缩仿射变换的组合称为迭代函数系统（IFS），即：

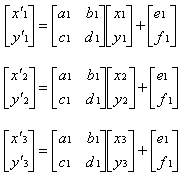
　　当然，上面各个变换W的系数应保证W是收缩仿射变换。

　　分形几何学中有一个定理：每一个迭代函数系统都定义了一个的分形图形，这个分形图形称为该迭代函数系统的吸收子（attractor）。这个定理称为收缩影射不动点原理。典型的例子是一片蕨子叶却所对应的迭代函数系统：

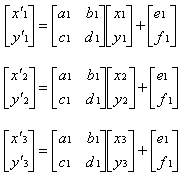
　　它所定义的蕨子叶如图2.2所示。从这个例子可看出，要产生一个复杂的图形需要得数据并不多。蕨子叶对应的迭代函数系统只有24个系数。如果以8比特代表一个系数，那么192比特就可以代表一片蕨子叶。可见压缩比是很大的。分形图象压缩的提出者之一邦利斯曾经扬言，他实现过10000:1的压缩。是否夸大不得而知，但分形压缩很有潜力却是无疑的。

　　2.3 采用迭代函数系统的图像压缩方法

　　从蕨子叶的例子可看出，迭代函数系统用不多的系数就可以代表一幅图像，从而得到很大的压缩比。但在实用时，如何寻找一的图像的迭代函数系统呢？目前有两个办法；一是基于图像的自相似性，直接计算迭代函数系统各收缩仿射变换的系数、二是把图像分割成教小的部分，然后从迭代函数系统库中查找这些小部分所对应的迭代函数系统。图2.3（a）是一个谢尔品斯基垫，可以看出，整个垫子是由上、左下、右下3个较小的垫子组成。每个较小的垫子是由原来的垫子经收缩仿射变换得来的。如果能分别找出把原图形变成3个小图形的收缩放射变换，那么，整个迭代函数系统就定下来了。

　　通过迭代，可以发现有向一个单一点收缩和会聚的一个集合。在这种情况下，会聚到的这个点叫做吸引不动点。反过来说，迭代也可以表现得从一个单一点发散；这种情况叫不稳定不动点。

　　当轨道的点会聚于一个或多个极限的时候，轨道的会聚点的集合叫做极限集合或 ω-极限集合。引和排斥的想法类似推广；依据在迭代下小邻域行为，可把迭代分类为稳定集合和不稳定集合。其他极限行为也有可能；

　　设原来垫子3各顶点的坐标分别为（x1,y1），（x2,y2），（x3,y3）。变换所得小垫子的3个顶点坐标为（x'1,y'1），（x'2,y'2），（x'3,y'3）。图2.3（b）表示的是把原电子变为上面小垫子的坐标。把W1的变换式：

　　展开：

　　x'1=a1x1+b1y1+e1

　　y'1=c1x1+d1y1+f1

　　x'2=a1x2+b1y2+e1

　　y'2=c1x2+d1y2+f1

　　x'3=a1x3+b1y3+e1

　　y'3=c1x3+d1y3+f1

　　解这组方程得到变换W1的各系数。以图1.7所示各坐标点的数值代如以上方程组，得到。同理，利用左下方垫子和右下方垫子可求出变换W2和W3的系数。分别为：

　　a2=d2=0.5,b2=c2=e2=f2=0,a3=d3=0.5,b3=c3=f3=0,e3=1.

　　直接计算迭代函数系统各变换矩阵系数的方法只能用于那些局部与整体有自相似特性的图像，而许多图像是难以用上述办法寻找迭代函数系统的。但若能把整个图像分割成小片，而这些小片图像的迭代函数系统是已知的，同样也可以实现图像的压缩。办法就是事先建立一个分形库，原图像分割的小片可按库的目录去寻找相应的迭代函数系统。当然，如何自动把图像合理地分割成小片，分形图形如何适当地放大、缩小或旋转以使之与目标尽可能的重合等，都还有大量的工作要做。

　　3 分形图像压缩的实例

　　利用分形几何方法进行图像压缩的历史比传统方法要短的多，因此相对也没有传统方法那么成熟。目前，尽管还不如传统方法那样已经有了对活动图像进行图像压缩的软件、硬件，但对单幅图像的分形压缩方法已经出现了商品化得计算机软件。提供这种软件的公司是美国迭代系统公司（Iterated System Inc.）。他们提供的软件名叫SuperBase Fractal Picture Linkers，这是一个配合SuperBase数据库系统的软件。它可以把画面进行压缩，得到的图形文件称为分形图像格式（Fractal Image Format，FIF），也可以把FIF文件解压成原有图像。

　　对程序开发人员，迭代系统公司还有POEM Colorbox Ⅲ和POEM Videobox等软件，前者使开发人员能够在微软视窗下把FIF文件集成到普通应用软件内，后者则可对MS-DOS上运行的应用软件中的图像进行压缩或解压。

　　4 分形图像压缩有待研究的问题

　　分形图像压缩是有失真的，失真量大小与压缩比密切相关。尽管分形图像压缩有巨大的潜力，但要把这种潜力释放出来，还有许多问题有待进一步的研究，主要表现在：

　　普遍性问题。对于一定的整体与局部存在明显相似性或仿射性的分形图像类，分形图像压缩方法的压缩比极高，但难以期望在很低的失真条件下，对一切分形图像压缩都具有极高的压缩比，只能在压缩比与失真度之间加以平衡。

　　就目前分形压缩技术而言，其编码时间比较长。因此，需要开发编码时间短、效率高的分形压缩算法。

　　理论上，有关自动压缩原理与算法，失真测度或相似性准则等有待继续深入研究。

　　实用化编码方法与硬件实现。

　　总之，分形理论用于图像压缩之所以有效，是因为自然界中普遍存在着分形物体，它们表面上具有非常复杂的统计特性和视觉特性，但信息量却很少，可用几条简单的确定规则迭代出来。传统的建立于信息论之上的图像压缩技术几乎不能压缩这类图像。而使用分形编码，只需对少数几条变换规则进行编码，即可以获得非常高的压缩比。但另一方面，由于自然界的景物千差万别，因此分形压缩尚有许多问题有待人们深入研究。