仪器的输出和各作用件的参数之间的关系如果能用数学关系表达,称这种关系式为作用方程式或仪器方程式。在具有明确的作用方程式的情况下,直接用微分法可以进行误差分析和计算。例如图1所示的自准直仪测角误差中,除原理误差外,还存在制造误差。那么,自准直仪的测角误差与哪些零件的制造误差有关呢?由式(4-2)得
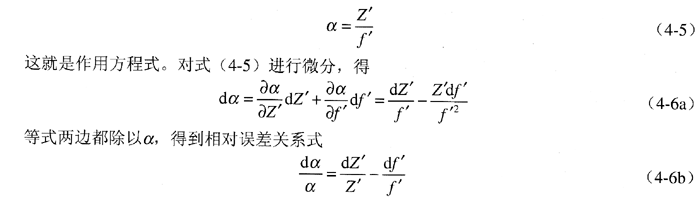
式中,右边项是分划板刻线误差;第二项是物镜焦距误差。式(4-6)不仅指出了测角误差与哪两项制造误差有关,而且还揭示了这两项误差的影响符号相反。因此在制定零件的公差时,可以考虑一个给正偏差,另一个给负偏差,这样可使它们对仪器测角误差的影响起到某种程度的抵消作用。
使用微分法时要注意实际仪器还有一些误差未包含在作用方程中,需另外计算。
欢迎转载,信息来源维库电子市场网(www.dzsc.com)
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。