IIR滤波器系数的计算

　　在经典的IIR滤波器设计中，数字滤波器的设计是非常接近理想滤波器的。理想数字滤波器模型规范在数学上转换成一组模拟滤波器模型的规范，所采用的方法为下面公式给出的双边z变换：

　　经典模拟Butterworth、Chebyshev或者是椭圆模型都可以由这些规范合成。然后利用双边线性z变换映射到数字IIR滤波器中。

　　模拟Butterworth滤波器的幅值平方的频率响应如下：

　　｜F（ω）｜2的极点沿着圆周分布，分别相隔冗胛弧度。再具体地说就是传递函数在ω＝0处N次可微。这一结论说明传递函数在0 Hz附近是局部光滑的。图1（上图）给出了—个Butterworth滤波器模型的例子。注意，这一设计的公差设计方案与Kaiser窗函数和图给出的equiripple设计是一致的。

　　图1 利用MATLAB工具箱的滤波器设计

　　（上）Btltterworth滤波器和（下）椭圆滤波器。

　　（a）传递函数 （b）通频带组延迟 （c）极点／零点分布图（×＝极点，O＝零点）

　　I型或者Ⅱ型模拟Chebyshev滤波器是按照Chebyshev多项式VN(ω)＝cos(JVcos(ω))定义的，这就要求滤波器的极点必须驻留在一个椭圆上。I型滤波器的幅值平方频率响应表述如下：

　　典型的I型滤波器示例的幅频和脉冲响应如图2（上图）所示。注意观察通带的纹波和光滑的抑止频带。

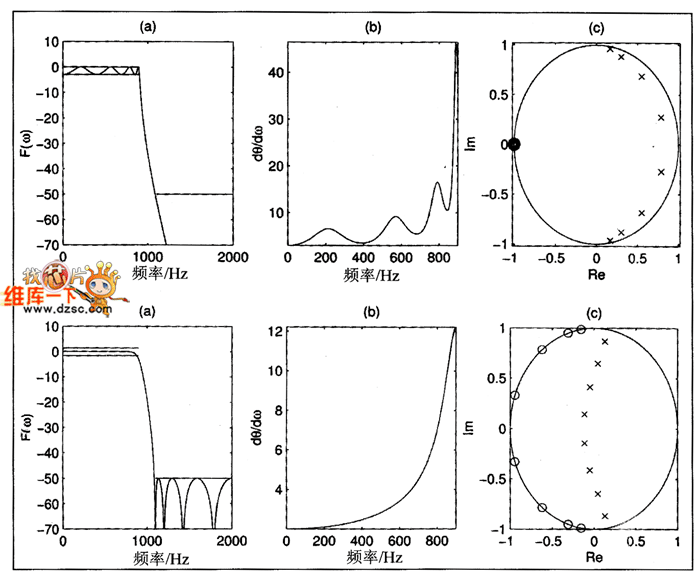
　　图2 利用MATLAB工具箱的Chebyshev滤波器设计

　　型滤波器。（a）传递函数 （b）通频带组延迟 （c）极点／零点分布图（×＝极点，o＝零点）

　　Ⅱ型滤波器幅值平方频率响应表述如下：

　　典型Ⅱ型的一个示例的幅值频率和脉冲响应如图2（下图）所示。注意：在该情况下会产生一个光滑的通频带，而抑止频带则呈现纹波特性。

　　模拟椭圆原型滤波器是根据Jacobian椭圆方程UN(＠)的解定义的。幅值平方频率响应的表述如下：

　　典型椭圆滤波器的幅值平方和脉冲响应如图1下图所示。注意观察椭圆滤波器在通频带和抑止频带表现出的纹波。
　　欢迎转载，信息来源维库电子市场网（www.dzsc.com）