感应电动机是 AC机器,其中交替电流直接通过定子的感应或变压器的作用直接向定子电枢绕组提供,并间接地向转子绕组。因此,它也称为旋转变压器。它的定子绕组与同步机的绕组相似。但是,感应电动机的转子可能是两种类型之一: 伤口转子具有三个绕组,类似于定子电枢绕组。转子绕组端子连接到安装在转子轴上的绝缘滑环。安装在这些环上的碳刷使机器操作员进入转子端子。在稳态操作期间,这些终端短路。 在松鼠式转子中,导电条固定在转子磁芯中的插槽中,并且通过传导末端环在两端都短路。由于转子条和短路环的形状像松鼠的笼子一样,因此将转子称为松鼠式转子。 大多数感应电动机都有松鼠笼转子,但是,从建模的角度来看,两种类型的转子相似。 应用于定子的三个平衡交替电压会导致平衡的定子电流流动。这些定子电流会产生一个旋转的MMF,可以将其表征为旋转磁场。根据法拉第的电磁诱导定律,这种旋转的磁场会在转子绕组中诱导电压。这些感应电压导致平衡电流流过短路转子。这些转子电流会产生转子MMF,也可以将其表征为旋转磁场。由于这两个旋转磁场之间的相互作用,产生了电磁扭矩,该扭矩 用于转动机械载荷T m。在稳态状态下,当电动机损耗被忽略时,T m 和T e 相等。 电机绕组是电感器,能量通过磁场存储在绕组中。 从定子上的固定位置看,转子磁场的旋转速度等于定子磁场的旋转速度,即同步速度N S。但是,转子速度n r 与同步速度不同。如果n r 等于n s,则转子中不会有通量连接的变化,否则不会有净通量切割;因此,转子不会诱导电压。因此,转子速度必须小于同步速度。速度的差异由滑动s表示,该速度被定义为: \ [s = \ frac {n_ {s} -n_ {r}} {n_ {s}}} \,\,\,(1)\] 在哪里 N R =转子速度(rpm) n s = \(\ frac {120f} {p} \)=同步速度(rpm) p =电线杆数 转子磁场的速度与以每分钟旋转表示的定子速度之间的差异称为滑动rpm,等于(N S - N R)。因此,转子电流的频率由: \ [f_ {r} = {\ big(} n_ {s} -n_ {r} {r} {\ big)}} \ frac {p} {p} {120} = s {\ big(} \ big(} 由于\(\ frac {pm_ {s}} {120} \)等于定子电流的频率,因此等式2也可以写为: f r = sf(3) 对于稳态操作,滑动值的正常范围在1%至5%之间。 在三相感应电动机中的等效电路的发展 在三相感应电动机的性能分析中,等效电路是无价的。因此,在本节中开发了等效电路以及近似等效电路。 三相感应电动机的等效电路的一般形式可以源自三相变压器的等效电路。感应电动机可以视为三相变压器,其次级或转子是短路的,并以运动速度旋转。由于电动机通常在平衡条件下运行,因此仅需要单相等效电路。 当平衡的三相电流在定子和转子绕组中流动时,所得的同步旋转气隙通量波会在定子绕组和转子绕组中诱导平衡的三相电压。定子引起的电压的频率等于施加电压的频率F,而转子诱导的电压的频率为频率F R, 由等式3给出。 首先考虑定子。跨定子端子的每个相的施加电压等于每个相的定子诱导的电压的总和,加上跨定子绕组电阻的电压降,以及由于泄漏通量引起的定子泄漏电抗的电压下降,这仅连接定子绕组。从数学上讲,以相位形式,这种关系可以表示为: V 1 = E 1 + R 1 I 1 + JX 1 I 1 = E 1 + I 1(R 1 + JX 1)(4) 在哪里 V 1 =每个阶段的定子端子电压 E 1 =每个相的定子诱导的电压 I 1 =每个阶段定子电流 R 1 =定子绕组电阻 x 1 =定子绕组电抗 可以将磁芯建模为电阻R C的平行组合 ,以解释磁滞和涡流损耗以及电抗X M ,以解释产生气隙磁通量所需的磁化电流。感应电动机中的磁化电流比变压器中的磁化电流大得多,因为电动机中存在气隙。 接下来,开发了转子的模型。令E 2 表示静止的转子诱导的电压,即s = 1.0。在停滞状态下,感应电动机可以被视为带有气隙的变压器,并且定子每相诱导的电压E 1 与转弯比(n 1 /n 2 )的 转子诱导的电压E 2有关: \ [e_ {1} = {\ big(} \ frac {n_ {1}}} {n_ {2}}} {\ big)} e_ {2} \,\,\,\,(5)\] 在哪里 n 1 =定子绕组中的转弯数 n 2 =转子绕组中的转弯数 感应电动机转子中诱导的电压与转子的相对运动和同步旋转的气隙磁场成正比。当感应电动机以速度n或滑动s旋转时,转子诱导的电压e 2s等于静止E 2 处的诱导电压 乘以滑动。在短路的转子电路中,诱导的电压E 2S 显示为跨转子电阻和泄漏电抗的电压下降。 转子电阻不取决于滑动。但是,转子泄漏电抗确实并且等于x r =2πfr l r = s2πflr ,其中 l r是由于 磁通量仅连接转子绕组而导致的转子绕组的泄漏电感。因此,滑动处的转子诱导的电压可以在数学上表示如下: e 2s = se 2 = i r r r r + j(2πfr l l r)i r = IRRR+JS2πflrir = i r r r + jsx 2'i r ( 6) 在哪里 e 2s =滑动s的转子诱导的电压 E 2 =转子在停滞处诱导电压(s = 1.0) i r =转子相电流 R R =每个相的转子电阻 x2'=2πflr =连续的转子泄漏抗性 将等式6的两侧除以滑动s,然后将转子数量引用到定子侧,如变压器中所产生 \ [e_ {2} = {\ big(} \ frac {r_ {r}} {s}+jx^{'} _ {2} {2} {\ big)} i_ {r} \ [{{\ big(} \ frac {n_ {1}} {n_ {2}}} {\ bigG)} e_ {2} = {\ bigG(} \ big(} \ frac {n_ {1}}}} \ big(} \ frac {r_ {r}} {s}+jx^{'} _ {2} {2} {\ bigG)} {\ bigG(} \ big(} \ frac {n_ {n_ {2}}}} \ [e_ {1} = {\ bigG(} \ frac {r_ {2}}} {s}+jx_ {2} {2} {\ bigG)} i_ {2}} \,\,\,\,\,\,\,(7)\,(7)\] 在哪里 e 1 =(n 1 /n 2)e 2 =转子诱导的电压转介给定子 i 2 =(n 2 /n 1)i r =转子电流转介给定子 r 2 =(n 1 / n 2)r 1 =转子电阻指的是定子 x 2 =(n 1 / n 2)2 x2'=转子泄漏电抗抗定子 以等式4表示的定子电路和公式7表示的转子电路在施加电压的相同频率F处。因此,这些定子和转子电路可以连接在一起,并将磁芯的模型结合到感应电动机的每相等效电路中,如图1所示。
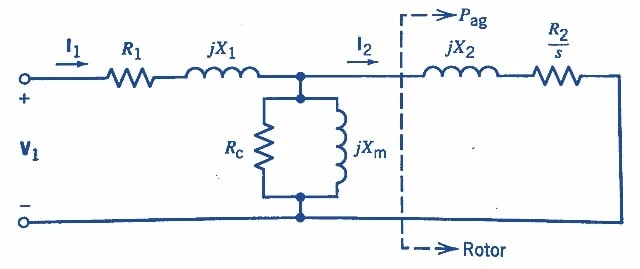
图1。 三相感应电动机的每一相等等效电路。图像由Amna Ahmad提供 通过并行移动分流元件r c 和x m来得出感应电动机的近似等效电路 ,代表电动机端子的。这种简化引入了很少的错误,但大大减少了计算工作。该近似等效电路如图2所示。图2所示,等效的转子电阻r 2 /s,已分解为r 2 和r 2 [(1-s) /s]。个电阻分量r 2表示转子铜损耗,第二个组件代表电动机开发的功率。

图2。 感应电动机的近似等效电路。图像由Amna Ahmad提供 感应发生器 就像直流和同步机一样,感应机可以用作发电机或电机。

