电力
电子转换器可以被视为由分段线性元件(电阻器、电感器和电容器等传统元件是特殊情况)以及电压和电流源、二极管和电子开关(如
晶闸管、
晶体管、MOSFET 等)组成。
在这种情况下,我们将电子设备 (ED) 称为具有分段线性电流-电压特性的任何电气或
电子元件,即使这可能是对术语的不使用。在许多实际中,电子设备可以建模为可变电阻器,它在导通状态下的非常低值和阻塞状态下的非常高的值之间变化。在其他情况下,可能需要使用更详细的半导体模型来表示器件。然而,在系统层面,特别是对于建模、仿真和控制设计,快速开关现象通常不是主要关注点。在这些情况下,将二极管和开关视为理想元件会更方便,假设它们在基本开路和闭路状态之间瞬间切换。
这一特性使系统模型具有混合性质,结合了离散和连续时间元素。因此,开关电子系统被归类为混合动力系统。这些系统通过多种拓扑或模式运行,具体取决于开关器件的状态。因此,有必要区分转换器的不同模式,为每种模式开发一个线性时不变的动态模型,并定义系统在模式之间切换的条件。此过程产生的模型通常称为开关模型,这是许多电源转换器
仿真器(如 PLECS)使用的框架。不幸的是,开关的条件可能取决于状态变量(称为内部控制的换向),这使得开关模型越来越复杂,即使对于相对简单的转换器拓扑也是如此。
一般来说,对于具有两个以上电子设备 (ED) 的转换器来说,构建一个涵盖所有可能工作条件的开关模型(称为完整的开关模型)变得非常具有挑战性。对于涉及以内部控制换向为特征的电子设备的转换器也是如此。这种情况的一个典型例子是断续导通模式,这是由于某些二极管的阻塞状态而发生的。
相反,互补模型很容易构建,并且可以捕获转换器的所有模式,无需列举它们,也无需假设模式序列和开关时间换向时刻的先验知识。构建电源转换器互补模型的关键思想是将非线性器件(包括二极管和开关)的电压-电流特性视为网络动态线性部分的输入-输出,这可以通过使用经典电路理论技术进行建模。然后用电子设备的特性完成模型。
构建电源转换器互补模型的方法包括将 ED 的特性与它们所属的电路分开建模,然后将这些表示与电路的动力学方程集成。在改进的节点分析中使用了类似的方法,这是 PSpice 等仿真程序中采用的建模技术,其中 ED 的特性由非线性平滑代数关系详细表示。相比之下,在这种方法中,假设 ED 是理想的,它们的特性由分段仿射关系表示,这是一种为了方便建模和仿真而选择的经典方法。
在这种方法中,功率转换器表示为线性时不变动态系统的反馈互连,表示为 Σd,它描述了电路拓扑,以及一组分段仿射特性 (φ, λ),表示电子设备 (ED) 的电流-电压特性(见图 1)。它在文学中也被称为 Lur'e 模型。
Σd 的状态空间表示可以根据电源转换器的配置,使用经典电路理论技术推导出来。

图 1:电路方程与器件特性的反馈互连(Lur'e 模型)非递减分段仿射 EDs 特性以互补形式表示,如上一篇文章 Introduction to Linear Complementarity Models for Switched Systems 所示。 构建动态块 Σ 的模型d,让我们将每个第 i 个电子设备 (ED) 上的电流和电压视为输入φ我或作为输出 λ我对于电路的其余部分,它表示系统的 Dynamic 部分。通过提取 Ns ED 获得的电路,由线性元件(电阻器、电感器、电容器)和外部源组成,在非常一般的假设下,可以用状态空间系统来描述:
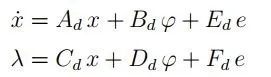
内部开关电路的互补模型
其中 x 是状态向量,e 表示外部源,φ 和 λ 是具有 Ns 个分量的向量,因此第 i 个分量对 (φi, λi) 表示第 i 个分量的特征。
二极管的线性互补模型 理想二极管 (ID) 的电压-电流特性如图 2 所示。它可以简单地用互补条件表示:
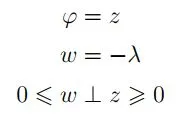
内部开关电路的互补模型
在对偶情况下,当 λ 是 ID 电流,φ 是 ID 电压时,可以通过更改公式 2 中两个相等值的右侧符号来获得互补模型。电路的拓扑决定了二极管电流应表示为 φ (从而影响状态变量的时间导数) 还是 λ (因此不进入状态的动态方程,而只满足代数方程)。
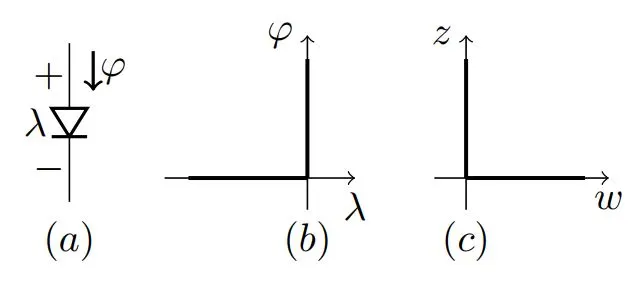
图 2:理想二极管:符号 (a)、电压-电流特性 (b) 和互补表示 (c)示例电路
为了展示这种建模技术在实际应用中的应用,我们可以考虑基于半波整流器的电源,如图 3 所示。
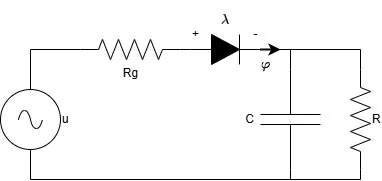
图 3:半波整流器电源
通过选择进入电容器的电流作为状态变量,选择二极管的互补表示,φ 为电流,λ 为电压,我们可以使用公式 2 编写电路的 Lur'e 表示:
内部开关电路的互补模型 由此,我们终可以推导出系统的线性互补表示(也称为线性互补系统):

内部开关电路的互补模型
通过离散方程 4,可以通过在每个积分步骤中求解相应的线性互补问题 (LCP) 来找到解。如图所示,单个方程组可以捕获电路的动态,无需详细说明二极管每种状态(导通或阻断)的每个等效电路。在经典仿真中(无论是可变步长还是固定步长),求解器必须检测状态切换(例如,通过电流或电压的过零),然后更新下一组方程和状态变量的初始值。然而,由于现代微处理器的计算能力,这种方法不再是问题。此外,所讨论的紧凑表示对于复杂电路的理论分析也很有价值,因为它可以将整个系统的动力学包含在一组方程中。
为了解决此类问题,已经开发了一种名为 Lemke 算法的特定算法。为了提高查找解的性能,可以在 Matlab 中使用另一个名为 “path” 的专用求解器。
仿真结果如下图所示:φ 和 λ 如图 4 所示,而在图 5 中,它们相对于其值进行了归一化,因此可以注意到它们是非负的,并且永远不会同时与零相差,因为它们对应于互补变量, 如图 2 所示。

图 4:互补变量
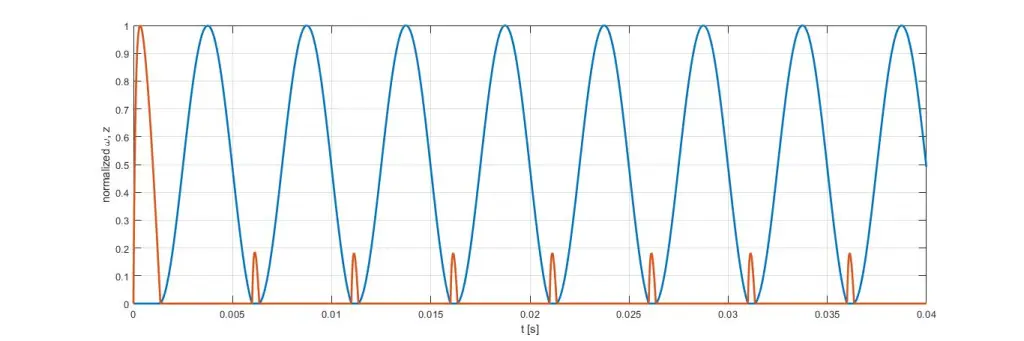
图 5:归一化互补变量
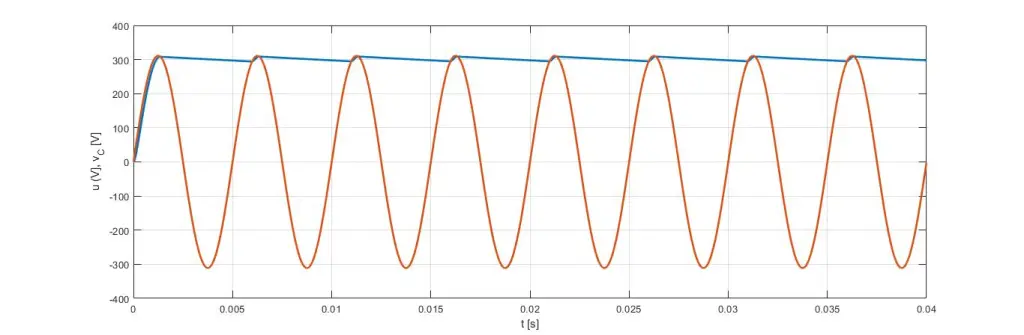
图 6:输入电压和电容器电压
 图 1:电路方程与器件特性的反馈互连(Lur'e 模型)非递减分段仿射 EDs 特性以互补形式表示,如上一篇文章 Introduction to Linear Complementarity Models for Switched Systems 所示。 构建动态块 Σ 的模型d,让我们将每个第 i 个电子设备 (ED) 上的电流和电压视为输入φ我或作为输出 λ我对于电路的其余部分,它表示系统的 Dynamic 部分。通过提取 Ns ED 获得的电路,由线性元件(电阻器、电感器、电容器)和外部源组成,在非常一般的假设下,可以用状态空间系统来描述:
图 1:电路方程与器件特性的反馈互连(Lur'e 模型)非递减分段仿射 EDs 特性以互补形式表示,如上一篇文章 Introduction to Linear Complementarity Models for Switched Systems 所示。 构建动态块 Σ 的模型d,让我们将每个第 i 个电子设备 (ED) 上的电流和电压视为输入φ我或作为输出 λ我对于电路的其余部分,它表示系统的 Dynamic 部分。通过提取 Ns ED 获得的电路,由线性元件(电阻器、电感器、电容器)和外部源组成,在非常一般的假设下,可以用状态空间系统来描述: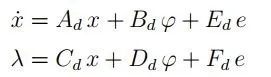
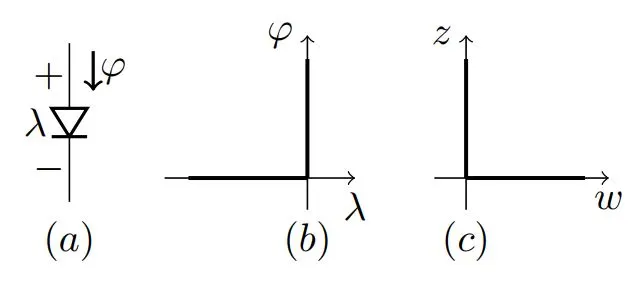 图 2:理想二极管:符号 (a)、电压-电流特性 (b) 和互补表示 (c)示例电路
图 2:理想二极管:符号 (a)、电压-电流特性 (b) 和互补表示 (c)示例电路 图 3:半波整流器电源
图 3:半波整流器电源

 图 5:归一化互补变量
图 5:归一化互补变量 图 6:输入电压和电容器电压
图 6:输入电压和电容器电压