使用分压器进行 RTD 测量
　　可以使用简单的电阻分压器将 RTD 电阻的变化转换为电压信号。图 1 显示了铂 RTD 的典型电路图。图中的 Pt1000 表示铂 RTD，在 0 °C 时标称电阻为 1000 Ω。

　　铂 RTD 的示例电路图。

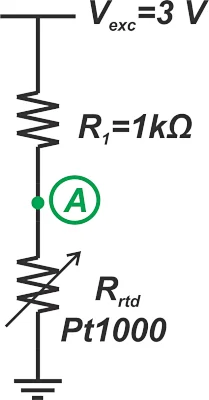
　　图 1. 铂 RTD 的示例电路图。
　　与大多数电阻传感器一样，RTD 传感器会随着测得的物理量的变化而变化相对较小的百分比。考虑到这一点，Pt1000 的温度系数约为 3.85 Ω/°C。 让我们看看节点 A 的电压变化有多大。
　　假设我们需要以 0.2 °C 的分辨率测量温度，这可能是一个相对苛刻的要求。如果温度从 0 °C 变为 0.2 °C，则传感器电阻从 1000 Ω 增加到 1000.77 Ω。因此，节点 A 的电压从 1.5 V 变为 1.500577 V，计算如下：
　　\[V_{A}=\frac{R_{rtd}}{R_{rtd}+R_{1}}\times V_{exc}=\frac{1000.77\times3}{1000.77+1000}=1.500577V\]
　　因此，温度变化 0.2 °C 会使节点 A 的电压变化约 577 μV。我们可以直接测量 V一个确定 RTD 电阻值和温度;但是，我们的测量系统应该具有足够的分辨率来检测 1.5V 信号中的几分之一毫伏变化。将 1.5 V 除以所需的步长 （577 μV），我们可以估算出模数转换器的无噪声计数，计算公式为：
　　\[噪声\，空闲\，计数=\frac{1.5V}{577 \mu V}\approx2600\，计数\]
　　这对应于大约 log 的无噪声分辨率2（2600） = 11.34 位。请注意，这仅给出了 A/D 分辨率的近似值。实际要求更为严格，取决于温度计设计的温度范围。此外，我们还以 3.85 Ω/°C 的恒定温度系数对 RTD 进行建模，而 RTD 实际上是非线性器件。
　　当今的 Δ-Σ （ΔΣ） 转换器可以轻松实现 11 位的无噪声分辨率。因此，我们可以使用图 1 中的电路以及 ΔΣ 转换器，直接对 RTD 两端的电压进行数字化处理。
　　然而，几十年前，这种高性能数据转换器不可用或不经济;电路设计人员使用 Wheatstone 电桥电路等技术进行 RTD 测量。虽然电桥电路仍常用于其他领域，例如力和压力传感应用，但它们很少用于 RTD 测量。尽管如此，为了完整起见，我们将在下面简要讨论电桥电路如何放宽模数转换器 （ADC） 的要求。
　　传统方法：使用惠斯通电桥进行 Pt1000 测量
　　用于 Pt1000 测量的基本惠斯通电桥如图 2 所示。

　　pt1000 的惠斯通电桥测量示例。

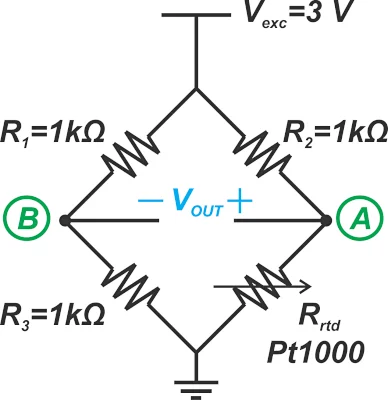
　　图 2. Pt1000 的惠斯通电桥测量示例。
　　输出电压是两个分支之间的电压差。事实上，桥式电路将单端测量从简单的分压器分支更改为差分测量。在这种情况下，当电桥平衡时（0 °C），输出为 0 V。如果温度升高 0.2 °C，则输出增加到 577 μV，计算如下：
　　\[V_{OUT}=V_{A}-V_{B}=\frac{1000.77\times3}{1000.77+1000}-\frac{1000\times3}{1000+1000}=577\mu V\]
　　在这种情况下，反映 RTD 电阻变化的所需信号不会位于较大的 DC 信号之上。输出仅包含我们要测量的信号。为了确定 ADC 的无噪声分辨率，我们应该考虑 V 的值和值外在温度计的整个温度范围内。假设我们需要测量 -40 °C 至 150 °C 的范围。在此温度范围内，RTD 电阻从 842.47 Ω 变为 1573.25 Ω。我们可以使用此信息来确定 V 的值和值外如下表 1 所示：
　　

表 1.

温度 （°C）	RRTD(Ω)	V外（五）
-40	842.47	-0.128249
150	1573.25	0.334159

　　由于应检测到的变化为 577 μV，因此系统的无噪声计数可通过以下方式计算：
　　\[噪声\，自由\，计数\，=\frac{V_{输出，}-V_{输出，}}{步\，大小}=\frac{0.334159-（-0.128249）}{577\mu V}\大约802\，计数\]
　　这对应于 9.65 位的无噪声分辨率。如您所见，基于电桥的测量在整个 190 °C 温度范围内获得的 ADC 分辨率仍然比分压器方法的单次测量所获得的分辨率要宽松。
　　RTD 应用的桥接电路限制
　　虽然桥式电路可以减轻 ADC 的要求，但这种方法有一些缺点。bridge output 取决于 bridge 配置中使用的 resistor 值。这种限制就是为什么需要三个精密电阻器来完成电桥的原因。除此之外，具有单个传感元件的电桥是非线性的。因此，除了 RTD 非线性之外，设计人员还必须补偿电桥的非线性响应。软件或模拟技术可用于线性化电桥电路，从而增加系统的复杂性。使用桥式电路时，我们还需要具有大共模抑制能力的仪表放大器，这些放大器可以提供高且相等的输入阻抗。
　　由于这些限制，并注意到现代 Δ-Σ 转换器可以轻松满足和击败 RTD 应用的要求，因此电路设计人员通常不使用桥式电路进行 RTD 测量。
　　使用 Delta-sigma 转换器进行 RTD 传感器测量图 3 显示了 RTD 传感器与 ΔΣ ADC 接口的简化图。

　　RTD 传感器和 ΔΣ ADC 接口的简化图

　　图 3. RTD 传感器和 ΔΣ ADC 接口的简化图
　　使用 22 位 ADC 且参考电压为 3 V 时，LSB（有效位）等于 \（\frac{3}{2^{22}}\approx0.72\，\mu V\）。
　　对于这些高分辨率 ADC，可检测信号通常受到 ADC 内部电子噪声的限制，例如内部电路产生的热噪声和闪烁噪声，而不是 ADC 的量化噪声。如果您需要复习 ΔΣ ADC 的噪声性能，可以参考德州仪器 （TI） 的这个由 12 部分组成的文章系列。
　　ΔΣ ADC 的峰峰值输入参考噪声可以达到微伏或更低的数量级。假设 ADC 的输入参考噪声为 3 μVp-p.对于图 3 中的电路，我们可以找到 RTD 电压的值和值 Vrtd，如下表 2 所示：
　　表 2.
　　温度 （°C）RRTD(Ω)VRTD（五）
　　-40842.471.3717
　　1501573.251.8342
　　利用这些信息，我们可以计算系统在 -40 °C 至 150 °C 温度范围内的无噪声计数，如下所示：
　　\[噪声\，空闲\，计数\，=\frac{V_{输出，}-V_{输出，}}{输入引用\，噪声}=\frac{1.8342 - 1.3717}{3\mu V}=154166\，计数\]
　　将温度范围除以无噪声计数，得到温度测量分辨率：
　　\[温度分辨率=\frac{T_{max}-T_{min}}{噪声\，自由\，计数}=\frac{150-（-40）}{154166}=0.0012°C\]
　　虽然这种精度水平实际上令人兴奋，但应该注意的是，其他几个误差源阻止了我们实现如此高的性能。R 的初始公差和温度漂移1ADC 失调电压和失调漂移是其中的一些误差源。然而，上述计算证实，现代 ADC 的噪声性能和分辨率足以实现精密测温;但是，设计人员需要消除其他主要误差因素以保持系统准确性。