信号反射是RF系统中通常遇到的现象,可以降低达到负载的功率。在设计一系列RF块时,波浪反射会导致有关级联在终设计中将显示多少功率增益的不确定性。为了更好地理解这一点,让我们介绍不匹配损失(ML),这是表征波浪反射引起的功率损失的参数。
不匹配损失公式
当传输线的输入和输出端口都连接到错配的阻抗(z ≠ z 0 和z l ≠z 0)时,输入端口和输出端口之间来回反弹的功率的一部分(图1)。 示例显示了传输线的输入和输出端口,这些端口通过不匹配的阻抗连接。
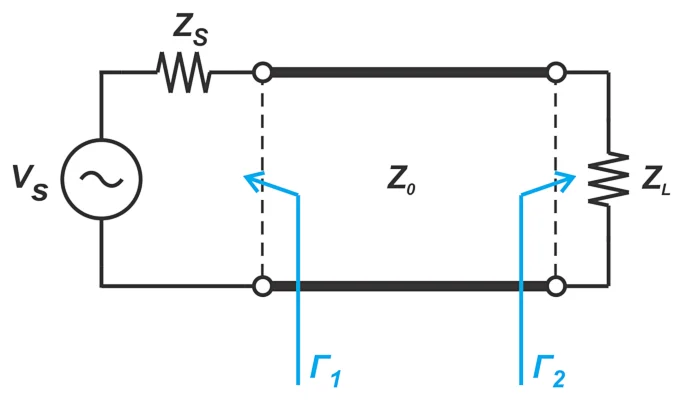
图1。 显示传输线的输入和输出端口,通过不匹配的阻抗连接。
这种波反射导致损失的功率,其特征是ML参数,如等式1所示。
\ [Ml = \ frac {| 1- \ gamma_1 \ gamma_2 |^2} {\ big(1- | \ gamma_1 |^2 \ big)等式1。
在许多应用中, γ1 和γ2的相角 尚不清楚。在这些情况下,我们只能找到ML的上和下限,以确定功率传递不确定性的范围。公式2和3分别显示ML的上和下限。
\ [ml_ {max} = \ frac {| 1+ | \ gamma_1 \ gamma_2 ||^2} {\ big(1- | \ gamma_1 |^2 \ big)\ big(1- | \ gamma_2 |^2 |^2 \ big)} \] \]
等式2。
\ [ml_ {min} = \ frac {| 1- | \ gamma_1 \ gamma_2 ||^2} {\ big(1- | \ gamma_1 |^2 \ big)\ big(1- | \ gamma_2 |^2 |^2 \ big)} \] \]
等式3。
在分贝中表达这两个一个方程并找到差异会产生不确定性范围,如等式4所示。
\ [mu = 20log \ big(1+ | \ gamma_1 \ gamma_2 | \ big)-20log \ big(1 - | \ gamma_1 \ gamma_1 \ gamma_2 | \ big)\] \]
等式4。
在RF文献中,这种不确定性范围称为不匹配不确定性(MU)。
不匹配损失和不确定性示例1:检查传输线效应为了更好地理解上述概念,我们使用LTSpice用参数z S = z L =50Ω和z 0 =75Ω来模拟图1中的电路。 LTSpice示意图如图2所示。 示例LTSpice示意图。
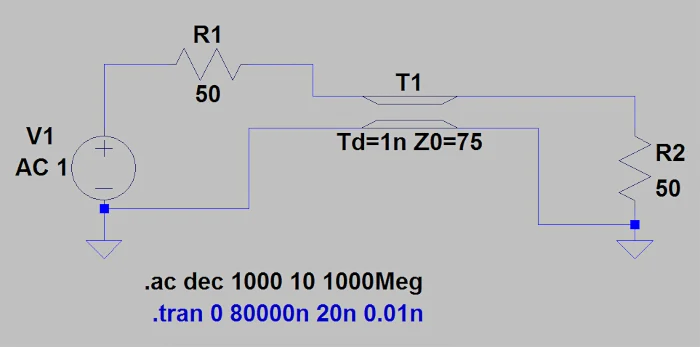
图2。 示例LTSpice示意图。
传输线的传播延迟为1 ns。这是表达传输线的物理长度的方便方法:波动沿线长度传播所需的时间。接下来,我们将AC源的频率从10 Hz扫到1 GHz,以找到负载电压和电流。使用此信息,我们可以找到在图3中提供的负载中消散的功率。 示例图显示了负载中消散的功率。
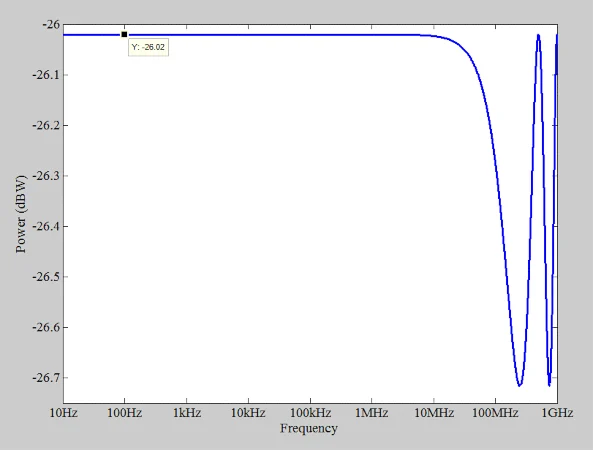
图3。 示例图显示了负载中消散的功率。
例如,在低频下,低于10 MHz的频率,传输线效应可以忽略不计,就好像负载直接连接到
信号源一样。在这种情况下,输入电压的一半出现在整个负载(V负载 = 0.5 V)上,并且输送到负载的功率被发现为:
\ [p_ {load} = \ frac {v_ {load}^2} {2z_ {l}} = 2.5 \ text {} mw = -
26.02 \ text {} dbw \]
这与上述图是一致的。随着我们增加频率,传输线效应会自我表现出来。另外,反射系数的相角(在距阻抗不连续性的固定距离处)随输入频率线性变化。因此,从等式1中,我们期望消散的功率随频率而变化。通过使用线性X轴绘制功率曲线,说明这一点,如图4所示。 示例图使用线性X轴显示功率曲线。

图4。 使用线性X轴显示功率曲线的示例图。
随着输入频率的变化,消散的功率会以循环方式上升和下降。曲线的个值发生在500 MHz。您可能想知道:为什么我们的值为500 MHz?
在我们的示例中,事件波到达线路并反射回源的往返时间为2 ns。另一方面,500 MHz信号的周期也为2 ns。因此,使用500 MHz信号,反射波与入射波相相添加,从而化功率传递。
请注意,在此直观的解释中,还应考虑反射系数的相角。但是,在我们的示例中,反射系数为负的真实值(γ1 = γ2 = -0.2),可以在500 MHz处进行建设性干扰。
考虑到这一点,方程1及其限制与图4中的曲线有关? MU(方程4)是ML的上限和下边界之间的差异。因此,它为我们提供了负载功率的总变化。如果我们将γ1=γ2= -0.2替换为 公式4 ,则不匹配的不确定性对MU = 0.7 dB起作用。这与图4中功率曲线的峰值变化是一致的。
参考功率对于不匹配损失很重要
我们在上面讨论了方程1的特征是阻抗不连续性引起的功率损失。此描述没有提供重要的信息:当没有错配引起的功率损耗(ML = 1或0 dB)时,我们希望系统将系统输送到负载。换句话说,我们不知道计算损失项的参考功率。如果您浏览方程1的推导,您会注意到参考功率是源P AV 的功率。源可用的功率是源传递的功率到连接匹配的负载。当γ2 =γ1 *时发生这种情况,其中 *表示复杂的共轭操作。用线性术语表示ML(而不是分贝),P AVS 与传递的功率P负载之间的关系 是通过公式5给出的。
\ [p_ {load} = \ frac {p_ {avs}}} {ml} \]
等式5。
请注意,使用γ2 = γ1 *,公式1产生ml = 1。这意味着当载荷连接匹配时,损耗项消失了ml = 1(或0 dB)。为了更好地理解这些概念,让我们检查另一个LTSpice模拟。
不匹配损失和不确定性示例2:使用交流分析
考虑图5中的以下图。 一个示例图,其中源和负载阻抗具有真实和虚构的零件。

图5。一个示例图 ,其中源和负载阻抗具有真实和虚构的零件。
在这种情况下,源和负载阻抗既具有真实和虚构的部分。我们可以使用交流分析来扫描输入频率并观察消散功率的变化。但是,在此示例中,我们将使用另一种(实际上更有趣的)方法:我们将在通过一系列值范围内扫描传输线的延迟时保持输入频率恒定。在198.943 MHz时,40 NH
电感器的阻抗为J50Ω。我们将以此频率检查电路,仅仅是因为它会产生一些容易使用的数字。 LTSpice示意图如图6所示。 图5中的LTSpice示意图。
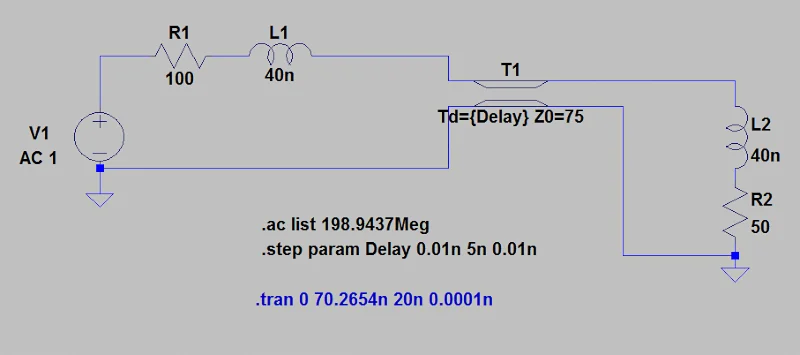
图6。 图5中的示例的LTSpice示意图。
请注意,传输线延迟定义为参数(“延迟”)。使用.step命令,“延迟”参数从
0.01 ns线性扫描到5 ns,步骤为0.01 ns。另外,使用“列表”选项,仅以单个频率(198.943 MHz)执行AC分析。 AC输入的幅度为1 V,正如AC模拟中常见的那样。该模拟为我们提供了负载电压和电流。使用这些信息,我们可以找到输送到负载的平均功率,如下蓝色曲线所示(图7)。 图显示了输送到负载的平均功率。
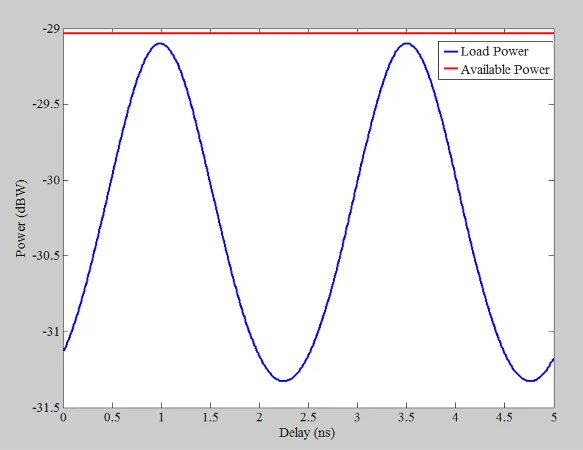
图7。 图显示了输送到负载的平均功率。
同样,我们可以使用对数刻度x轴更好地观察电路响应的延迟值很小。这如图8所示。 使用对数刻度绘制X轴以进行电路响应。
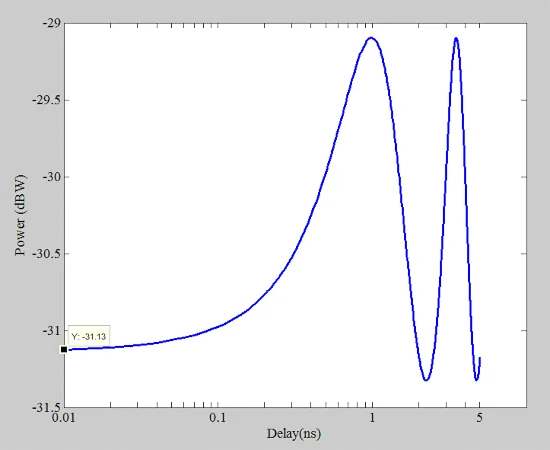
图8。 使用对数刻度进行电路响应的X轴绘图。
现在,让我们使用我们的方程式来验证上述曲线。在此之前,我们需要以感兴趣的频率找到等效电路(198.943 MHz)。在此频率下,40 NH
电感器具有J50Ω的阻抗,从而导致图9的以下图。 具有关注频率的等效电路的示例图(198.943 MHz)。
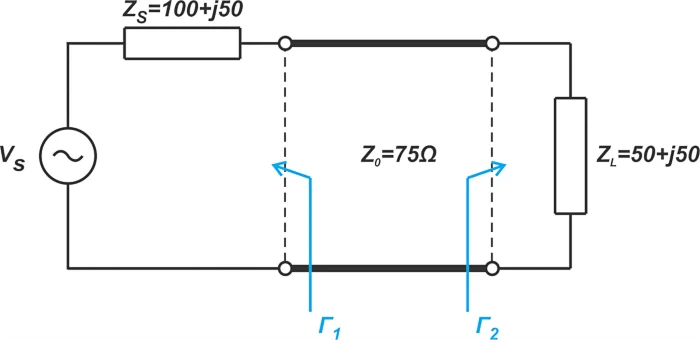
图9。 具有关注频率的等效电路的示例图(198.943 MHz)。
个问题是:为什么负载功率会随着行延迟的函数而变化?从下面的公式6可以看出,在线的载荷端(γ2)处的载荷反射系数在给定频率下是恒定的:
\ [\ gamma_2 = \ frac {z_l -z_0} {z_l+z_0} = \ frac {(50+j50)-75} {(50+j50)+75} = 0.415等式6。
但是,即使有无损线,反射系数的相角沿线变化。相角的这种变化决定了在线的源端的建设性或破坏性的入射波和反射波是否会进行干扰。通过扫描传输线的延迟,反射系数的相角以及传递到负载的功率的变化。
下一个问题:在传输线效应可忽略不计的延迟值时,将多少功率传递?图8显示,对于小于0.03 ns的延迟,负载功率几乎是恒定的。在此延迟范围内,传输线效应几乎可以忽略不计,好像负载直接连接到源(图10)。 图显示了直接连接到源的负载。
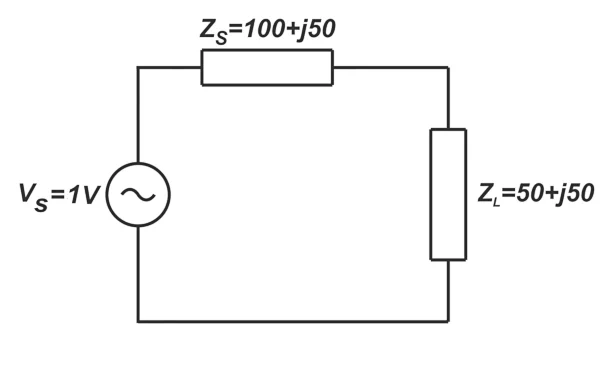
图10。 显示直接连接到源的负载的图。
使用基本电路理论概念,您可以验证上述电路向负载提供的平均功率是0.77 MW或-31.13 dBW。这与图8一致。源可以输送到偶联负载的功率是多少?使用Z S = 100+J50的源阻抗,使用等式7发现了1 V源的功率。
\ [p_ {avs} = \ frac {v^2} {8r_s} = \ frac {1^2} {8 \ times 100} = 1.25 \ text {} mw = -29.03 \ text {}
等式7。
这是源可以为共轭匹配负载提供的功率。在我们的电路中,载荷不是源阻抗的共轭物,因此,消散功率始终低于P AV (图7中的红色曲线)。使用等式2和3,我们可以找到不匹配损失的限制。我们首先需要使用公式8 找到γ1 。
\ [\ gamma_1 = \ frac {z_s -z_0} {z_s+z_0} = \ frac {(100+j50)-75} {(100+j50)+75} = 0.307等式8。
将γ1和γ2取代到 方程2 和3中,ML min = 0.07 dB,ML值 = 2.29 dB。从可用功率(-29.03 dbw)中减去这些值,使我们的值和值P l,max = -29.1 dbw和p l,min = -31.32 dbw。这些值也与图7中功率曲线的和值一致。









