第 2 部分将重点介绍全波整流。

　　图片由 Adobe Stock 提供
　　全波整流
　　全波整流发生在负周期和正周期中。换句话说，整流是在一个完整的周期中进行的。在现代电子学中，存在两种全波整流配置，桥式全波整流器和中心抽头全波整流器。两者都有其优点和缺点。

　　Center-Tzeed Rectifier （中心抽头整流器）

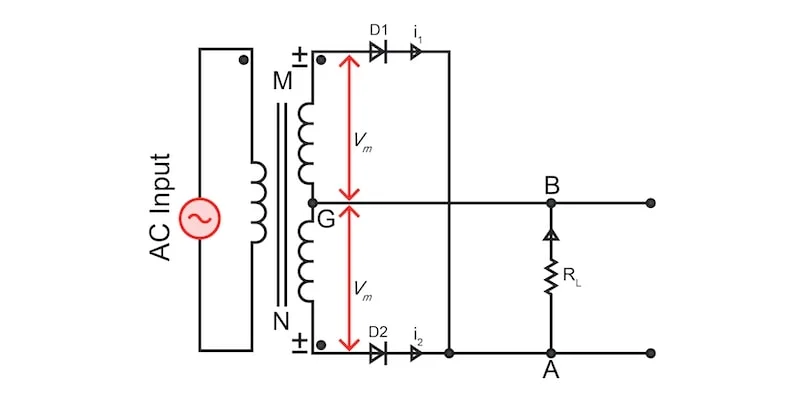
　　图 1.中心抽头整流器的中心图。图片由 Simon Mugo 提供
　　这种类型的全波整流涉及中心抽头变压器次级电压，其中每个线圈端接不同的二极管 D1 和 D2，中心抽头接地。
　　此整流中使用的中心抽头变压器的显着特点是：
　　中点分接电压为零，形成中性点。
　　这种分接是通过在变压器次级绕组的中心连接一根引线来进行的。在这种情况下，线圈将被分成两相等的部分。
　　这种抽头将输出电压分成两个具有不同极性的相等量。
　　您可以执行多次分接，从而提供不同数量的输出电压。
　　中心抽头全波整流的工作原理

　　通过向变压器施加正的半周期电压，变压器次级绕组的 M 点变为正。该动作使二极管 D1 正向偏置，导致电流 i1流经点 A 到 B，这是一条穿过负载电阻 R 的路径L.输出产生一个正的半周期。下面的图 3 是该解释的电路表示。

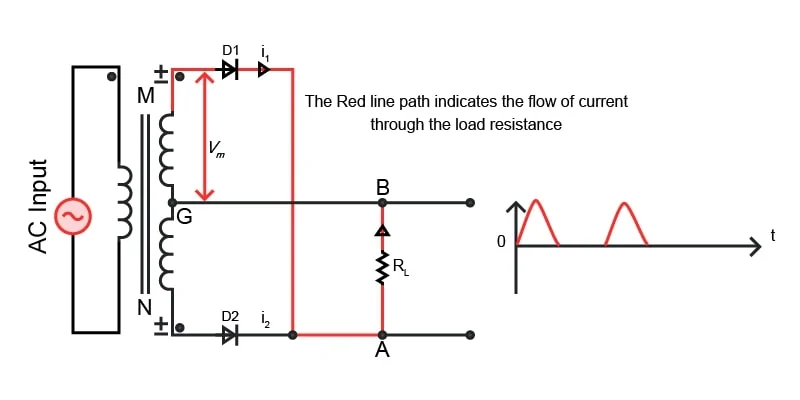
　　图 2.指示正半周期电流的电路。图片由 Simon Mugo 提供

　　在变压器半周期的次级绕组上施加负输入时，变压器次级绕组的点 M 变为负值。二极管 D1 终是反向偏置的，D2 是正向偏置的。正向偏置二极管 D2 允许电流 i2流过负载电阻 Rl从 A 点到 B 点。此操作会导致 output 处出现正半周期，即使 input 为负半周期。

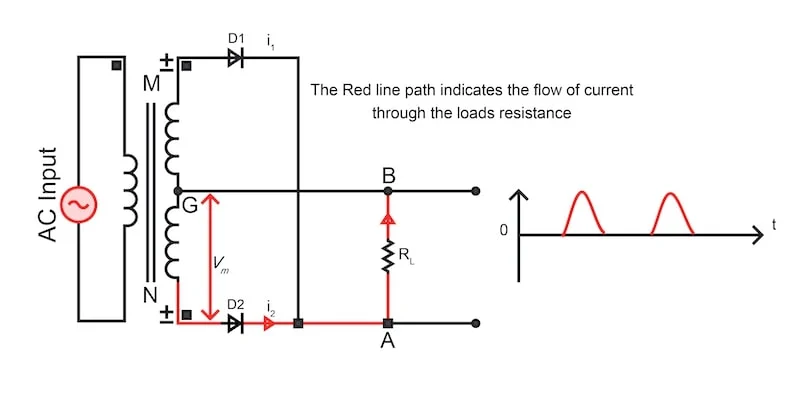
　　图 3. 指示负半周期电流的电路。图片由 Simon Mugo 提供

　　中心抽头全波整流器波形

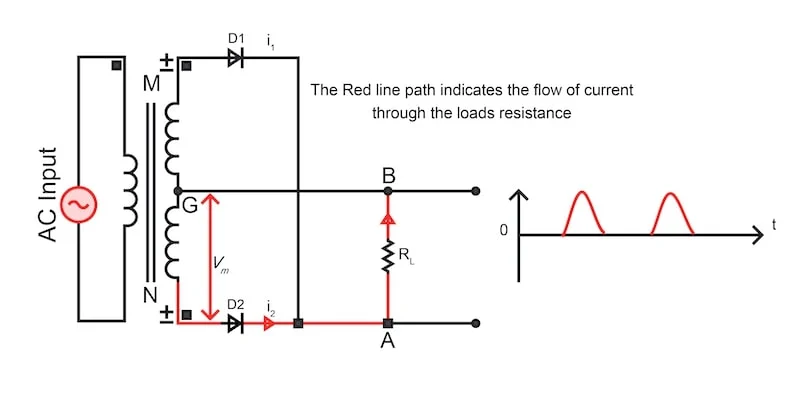
　　图 4.中心抽头全波整流器波形。图片由 Simon Mugo 提供
　　图 4 显示，输出来自负半周期和正半周期，并且两个整流器半周期的输出方向相同。
　　中心抽头全波峰值反向电压
　　变压器半次级铜绕组两端的电压由 V 决定m，并且整个次级电压出现在 nun 导电极二极管上。因此，峰值反向电压是变压器半次级绕组两端电压的两倍。
　　峰值反向电压可由以下公式确定：
　　\[PIV=2V_{m}\]
　　中心抽头全波整流器的缺点包括：
　　难以找到中心敲击
　　小输出直流电压
　　二极管的 PIV 必须非常高
　　桥式整流器
　　该电路使用四个二极管，不仅可以产生全波整流，还可以解决与中心抽头配置相关的缺点。

　　二极管 D1、D2、D3 和 D4 连接在一起，因此在任何给定的半个周期中只有两个二极管导通。不涉及中心敲击。

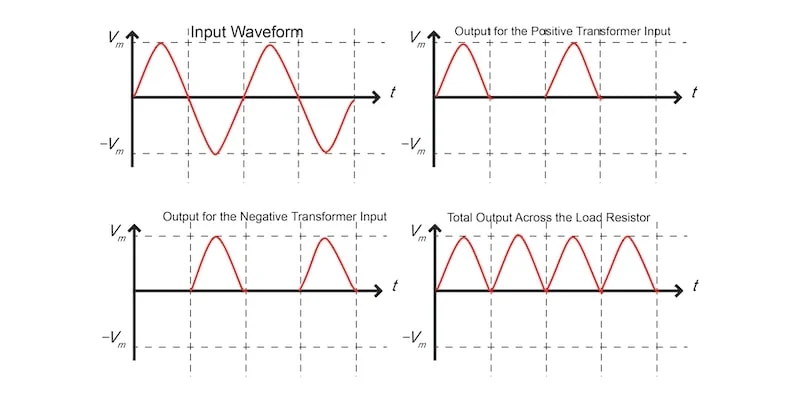
　　图 5. 桥式全波整流器的电路图。图片由 Simon Mugo 提供
　　Bridge Full-Wave Rectification 的工作原理

　　向电桥输入一个正的半周期，与点 Q 相比，P 点变为正。这使得二极管 D1 和 D3 正向偏置，而二极管 D2 和 D4 保持反向偏置。二极管 D1 和 D3 与负载电阻形成串联连接并完成导通回路，如图 6 所示。现在两个二极管一起工作产生输出，产生的电压将是中心抽头全波整流器的两倍。

　　图 6.正输入电流指示电路。图片由 Simon Mugo 提供

　　与点 Q 相比，在电路的输入点注入负半周期会使 P 点变为负值，从而使二极管 D1 和 D3 反向偏置，而二极管 D2 和 D4 变为正向偏置。二极管 D2 和 D4 形成一个串联环路负载电阻并进入导通模式，如图 7 所示。

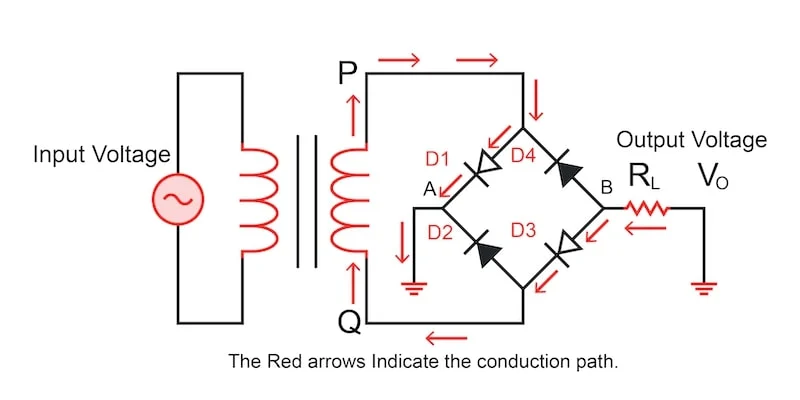
　　图 7.负输入电流指示电路。图片由 Simon Mugo 提供

　　电桥 FWR 的波形

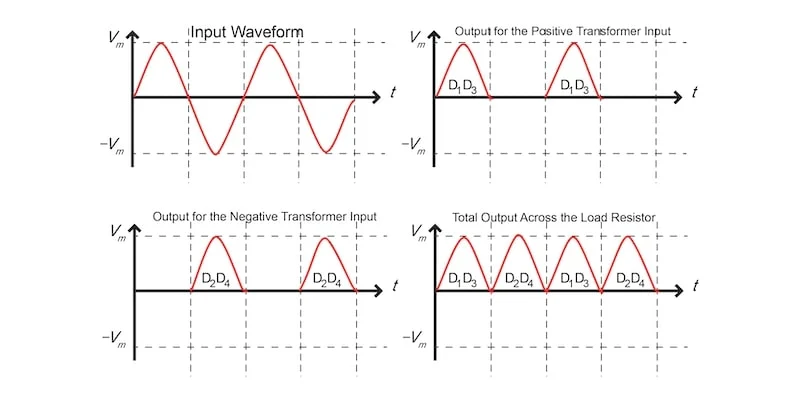
　　图 8. 桥式全波整流器波形。图片由 Simon Mugo 提供
　　图 8 显示了负半周期和正半周期获得的输出，并且两个半周期输出具有相同的方向。
　　桥式整流器解决了与中心抽头整流器相关的缺点。
　　全波整流器分析
　　为了实现分析，假设输入电压 V我将成为：
　　\[V_{i}=V_{m}sin\omega t\]
　　R 中的电流L或二极管由以下公式确定：
　　\[i_{1}=I_{m}sin\omega t\，\，\，for\，0\leq\omega t\leq\pi\]
　　\[i_{1}=0\，\，\，for\，\pi\leq\omega t\leq2\pi\]
　　哪里
　　\[I_{m}=\frac{V_{m}}{R_{f}+R_{L}}\]
　　同样，R 中的L或二极管由以下因素决定：
　　\[i_{2}=0\，\，\，for\，0\leq\omega t\leq\pi\]
　　\[i_{2}=I_{m}sin\omega t\，\，\，for\，\pi\leq\omega t\leq2\pi\]
　　通过负载电阻的总电流是所有电流的总和：
　　\[i=i_{1}+i_{2}\]
　　平均电流或直流电流
　　平均电流输出可推导出为：
　　\[I_{DC}=\frac{1}{2\pi}\smallint^{\pi}_{0}i_{1}d（\omega t）+\frac{1}{2\pi}\smallint^{2\pi}_{0}i_{2}d（\omega t）\]
　　替换 i 的方程1和我2完成集成后，我们发现
　　\[I_{DC}=\frac{2I_{m}}{\pi}=0.636I_{m}\]
　　与我们分析半波整流器时得到的值相比，该值是 2 倍。
　　输出直流电压
　　全波整流器的输出直流电压由以下公式确定：
　　\[V_{DC}=I_{DC}R_{L}=\frac{2I_{m}R_{L}}{\pi}=0.636I_{m}R_{L}\]
　　该值是半波整流器直流电压输出的两倍。
　　RMS 电流
　　RMS 电流的方程式可以推导出为：
　　\[I_{RMS}=\sqrt{\frac{1}{\pi}\smallint^{\pi}_{0}sin^{2}\omega t\，d（\omega t）}\]
　　如果两半中的两个电流在两半中相等，则方程变为：
　　\[I_{RMS}=\sqrt{\frac{I_{m}^{\，\，2}}{\pi}\smallint^{\pi}_{0}sin^{2}\omega t\，d（\omega t）}\]
　　\[I_{RMS}=\frac{I_{m}}{\sqrt2}\]
　　整流器的效率
　　\[\eta=\frac{输出\，DC\，Power\，of\，the\，负载}{输入\，AC\，Power\，from\，the\，变压器}=\frac{P_{DC}}{P_{AC}}\]
　　\[P_{DC}=（\frac{V_{m}}{\pi}）^{2}\]
　　\[P_{AC}=（\frac{V_{m}}{\sqrt2}）^{2}\]
　　在效率方程中替换上述内容，效率变为：
　　\[\eta=\frac{8}{\pi^{2}}=0.812=81.2\%\]
　　纹波系数
　　外形规格的计算方式如下：
　　\[F=\frac{I_{RMS}}{I_{DC}}\]
　　替换公式中的当前值，您得到的外形尺寸为 1.11
　　纹波因子现在由下式给出;
　　\[\gamma=\sqrt{F^{2}-1}\]
　　替换正确的值，纹波系数为 0.48。