计数器的工作是通过每个时钟脉冲将计数器的内容增加一个计数来进行计数。当由时钟输入激活时，增加其数字或状态序列的计数器被称为在“向上计数”模式下运行。同样，当由时钟输入激活时减少其数字或状态序列的计数器被称为在“向下计数”模式下运行。在向上和向下模式下运行的计数器称为双向计数器。
　　计数器是顺序逻辑设备，由外部定时脉冲或时钟信号激活或触发。计数器可以构造为同步电路或异步电路。使用同步计数器，所有数据位都会随着时钟信号的施加而同步变化。而异步计数器电路与输入时钟无关，因此数据位会在不同时间相继改变状态。
　　那么，计数器就是顺序逻辑设备，它遵循由外部时钟 (CLK) 信号触发的预定计数状态序列。特定计数器在再次返回其原始状态之前前进的状态或计数序列数称为模数 ( MOD )。换句话说，模数（或简称模数）是计数器计数的状态数，是计数器的分频数。
　　模数计数器（或简称为MOD 计数器）是根据计数器在返回其原始值之前将按顺序经过的状态数来定义的。例如，一个 2 位计数器以二进制从 00 2计数到 11 2，即以十进制从 0 到 3，其模数值为 4（00 → 01 → 10 → 11，然后返回到 00），因此被称为模 4 或 mod-4 计数器。还要注意，从 00 到 11 需要四个时钟脉冲。
　　由于在这个简单的例子中只有两位，（n = 2），那么计数器可能的输出状态的数量（模数）为：2 n = 2 2或 4。但是，可以通过将多个计数级级联在一起来设计计数器，使其按顺序计数到任意数量的 2 n状态，以产生单个模数或 MOD-N 计数器。
　　因此，“Mod-N”计数器需要“N”个触发器连接在一起来计数单个数据位，同时提供 2 n 个不同的输出状态（n 为位数）。请注意，N 始终是整数值。
　　我们可以看到，MOD计数器的模数值是2的整数幂，即2、4、8、16等，根据所用触发器的数量以及它们的连接方式产生n位计数器，从而确定计数器的类型和模数。
　　D型触发器
　　MOD 计数器使用“触发器”制成，单个触发器可以产生 0 或 1 的计数，计数为 2。我们可以使用不同类型的触发器设计，SR、JK、JK 主从、D 型甚至 T 型触发器来构建计数器。但为了简单起见，我们将使用 D 型触发器（DFF），也称为数据锁存器，因为使用单个数据输入和外部时钟信号，并且也是正边沿触发的。
　　D 型触发器（例如 TTL 74LS74）可以由基于 SR 或 JK 的边沿触发触发器制成，具体取决于您希望它在时钟脉冲的正沿或前沿（0 到 1 转换）还是负沿或后沿（1 到 0 转换）上改变状态。这里我们假设一个正沿、前沿触发的触发器。您可以在以下有关D 型触发器的链接中找到更多信息。

　　D 型触发器和真值表

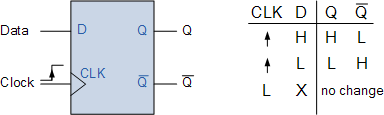
　　d型触发器
　　D 型触发器 (DFF) 的操作非常简单，因为它只有一个数据输入（称为“D”）和一个额外的时钟“CLK”输入。这允许在时钟信号的控制下存储单个数据位（0 或 1），从而使 D 型触发器成为同步设备，因为输入端的数据仅在时钟脉冲的触发沿传输到触发器输出。
　　因此，从真值表可知，如果在施加正时钟脉冲时数据输入端为逻辑“1”（高电平），则触发器将置位并在“Q”处存储逻辑“1”，并在Q处存储互补的“0”。同样，如果在施加另一个正时钟脉冲时数据输入端为低电平，则触发器将复位并在“Q”处存储“0”，并在Q处存储结果“1” 。
　　然后，当时钟 (CLK) 输入为高电平时，D 型触发器的输出“Q”将响应输入“D”的值。当时钟输入为低电平时，“Q”处的条件（无论是“1”还是“0”）将保持到下时钟信号变为高电平至逻辑电平“1”为止。因此，“Q”处的输出仅在时钟输入从“0”（低电平）值变为“1”（高电平）时才改变状态，使其成为正边沿触发的 D 型触发器。请注意，负边沿触发的触发器的工作方式完全相同，只是时钟脉冲的下降沿是触发沿。
　　现在我们知道了边沿触发 D 型触发器的工作原理，让我们看看如何将它们连接在一起形成 MOD 计数器。
　　二分频计数器
　　边沿触发 D 型触发器是一种实用且用途广泛的构建块，可用于构建 MOD 计数器或任何其他类型的时序逻辑电路。通过将Q输出重新连接到“D”输入（如图所示），并创建反馈回路，我们可以仅使用时钟输入将其转换为二进制二分频计数器，因为Q输出信号始终是 Q 输出信号的反相。

　　二分频计数器和时序图

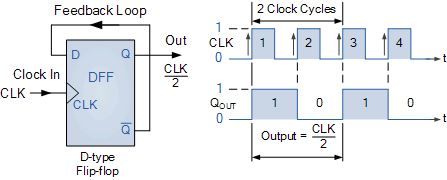
　　除以两个 mod 计数器
　　时序图显示“Q”输出波形的频率恰好是时钟输入的一半，因此触发器充当分频器。如果我们添加另一个 D 型触发器，使“Q”处的输出成为第二个 DFF 的输入，那么第二个 DFF 的输出信号将是时钟输入频率的四分之一，依此类推。因此，对于“n”个触发器，输出频率除以 2n，步长为 2。
　　请注意，这种分频方法在顺序计数电路中使用非常方便。例如，使用 60 分频计数器可以将 60Hz 主频信号降低到 1Hz 定时信号。6 分频计数器会将 60Hz 降低到 10Hz，然后将其馈送到 10 分频计数器，将 10Hz 降低到 1Hz 定时信号或脉冲等。
　　MOD-4 计数器
　　从技术上讲，单个触发器不仅是一种 1 位存储设备，而且可以将其视为 MOD-2 计数器，因为它只有一个输出，在施加时钟信号时，计数结果为 2，即 0 或 1。但单个触发器本身产生的计数序列有限，因此，通过将更多触发器连接在一起形成一个链，我们可以增加计数容量并构建任意值的 MOD 计数器。
　　如果单个触发器可以视为模 2 或 MOD-2 计数器，那么添加第二个触发器将为我们提供一个 MOD-4 计数器，使其能够以四个离散步骤进行计数。总体效果是将原始时钟输入信号除以四。然后，这个 2 位 MOD-4 计数器的二进制序列将是：00、01、10 和 11，如图所示。

　　MOD-4 计数器和时序图

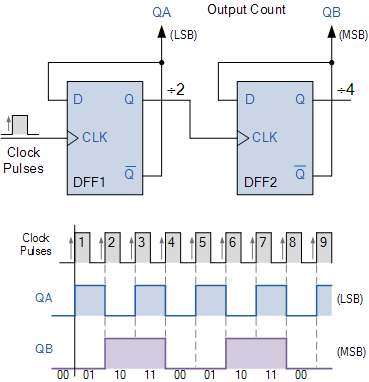
　　模数计数器
　　请注意，为简单起见，尽管此连接代表异步计数器，但上述时序图中 QA、QB 和 CLK 的开关转换显示为同时进行。实际上，在正向时钟 (CLK) 信号的应用与 QA 和 QB 的输出之间会有非常小的开关延迟。
　　我们可以使用真值表和状态图直观地展示这个 2 位异步计数器的操作。
　　MOD-4 计数器状态图
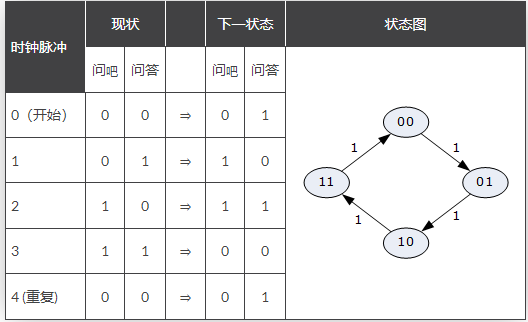
　　　　从计数器的真值表中我们可以看出，通过读取 QA 和 QB 的值，当 QA = 0 且 QB = 0 时，计数为 00。在施加时钟脉冲之后，值变为 QA = 1，QB = 0，计数为 01。在下一个时钟脉冲到来后，值发生变化并变为 QA = 0，QB = 1，计数为 10。值变为 QA = 1，QB = 1，计数为 11。施加下一个时钟脉冲导致计数回到 00，此后它按照二进制序列连续向上计数：00、01、10、11、00、01……
　　然后，我们看到 MOD-2 计数器由单个触发器组成，而 MOD-4 计数器需要两个触发器，这样它就可以以四个离散步骤进行计数。我们可以轻松地在 MOD-4 计数器的末端添加另一个触发器，以生成 MOD-8 计数器，从而为我们提供从 000 到 111 计数的 2 3二进制序列，然后再重置回 000。第四个触发器将构成 MOD-16 计数器，依此类推，事实上，只要我们愿意，我们可以继续添加额外的触发器。

　　MOD-8 计数器和状态图

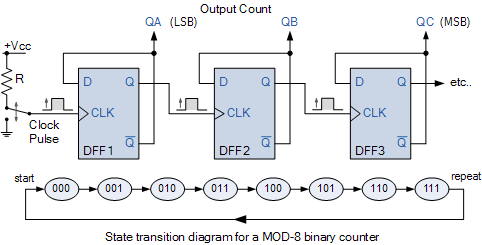
　　mod-8 mod 计数器
　　因此，我们可以构造模数计数器，使其具有 2n个状态的自然计数，从而给出模数计数为 2、4、8、16 等的计数器，然后再重复。但有时需要有一个模数计数器，它在正常计数过程中将其计数重置为零，并且没有 2 的幂的模数。例如，模数为 3、5、6 或 10 的计数器。
　　模“m”计数器
　　计数器（无论是同步计数器还是异步计数器）都按照一组二进制数列计数，因此“n”位计数器自然地充当模 2 n计数器。但是，我们可以构造模计数器来计数到我们想要的任何值，方法是使用一个或多个外部逻辑门，使其跳过几个输出状态并在任何计数时终止，将计数器重置为零，也就是说所有触发器的 Q = 0。
　　对于模数“m”计数器，它们不会计数到所有可能的状态，而是计数到“m”值，然后返回零。显然，“m”是一个小于 2 n 的数字，（m < 2 n）。那么我们如何让二进制计数器在计数过程中返回零呢？
　　幸运的是，除了计数（向上或向下）之外，计数器还可以具有称为CLEAR和PRESET的附加输入，这使得可以将计数清除为零（所有 Q = 0）或将计数器预设为某个初始值。TTL 74LS74 具有低电平有效的预设和清除输入。
　　为简单起见，我们假设 CLEAR 输入全部连接在一起，并且是高电平有效输入，当 Clear 输入等于 0（低电平）时，触发器可以正常运行。但如果 Clear 输入处于逻辑电平“1”（高电平），则时钟信号的下一个正边沿会将所有触发器重置为状态 Q = 0，而不管下一个时钟信号的值如何。
　　还要注意，由于所有清除输入都连接在一起，因此在计数开始之前，也可以使用单个脉冲将所有触发器的输出 (Q) 清除为零，以确保计数实际上从零开始。此外，一些较大位的计数器有一个额外的 ENABLE 或 INHIBIT 输入引脚，允许计数器在计数周期的任何时间点停止计数并保持其当前状态，然后再继续计数。这意味着可以随意停止和启动计数器，而无需将输出重置为零。
　　Modulo-5 模数计数器
　　假设我们要设计一个 MOD-5 计数器，我们该怎么做呢？首先我们知道“m = 5”，所以 2 n必须大于 5。由于 2 1  = 2、2 2 =  4、2 3 =  8，且 8 大于 5，所以我们需要一个至少有三个触发器 (N = 3) 的计数器，以便为我们提供 000 到 111（十进制为 0 到 7）的自然二进制计数。
　　使用上面的 MOD-8 计数器示例。其自然计数的真值表如下：

　　MOD-8 计数器和真值表

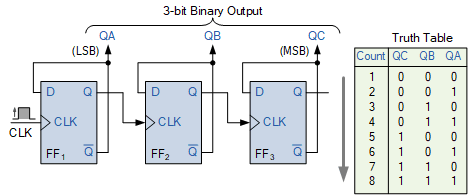
　　模数计数器和真值表
　　由于我们要构建一个MOD-5 计数器，因此我们需要修改上面的 3 位计数器电路，以便它在计数 5 后将自身重置回零。即计数序列为：1→2→3→4→5→重置，依此类推。
　　MOD-5 计数器将产生一个从 0 到 4 的 3 位二进制计数序列，因为 000 是有效计数状态，从而给出二进制计数序列：000、001、010、011、100。因此，我们需要计数器电路在下一个计数状态下重置自身，因为计数六（下一个计数）将产生输出条件：QA = 1、QB = 0 和 QC = 1（二进制），如下面的状态图所示。

　　MOD-5 计数序列

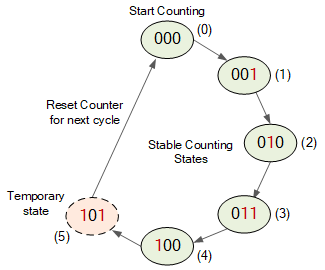
　　mod-5 计数序列

　　我们可以解码这个输出状态 101 (5)，借助 3 输入与门 (TTL 74LS11) 和反相器或非门 (TTL 74LS04)，给我们一个信号，将计数器清零 (Clr)。由反相器和数字逻辑与门组成的组合逻辑电路的输入分别连接到 3 位计数器输出：QA、QB 和 QC。

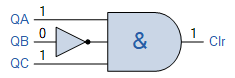
　　3输入与门
　　因此，除了我们想要的输入序列之外，对于任何输入组合，3 输入与门的输出都将处于逻辑电平“0”（低电平）。
　　以二进制代码表示，输出序列数将如下所示：000、001、010、011、100。
　　虽然计数器似乎一直计数到 101 状态，但当异步计数序列达到下一个二进制状态 101 (5) 时，组合逻辑解码电路将检测到此 101 条件，因此 AND 门将产生逻辑电平“1”(高电平) 输出，将计数器重置回其初始零状态。因此，计数器只能在此 101 临时状态保持几纳秒，然后重置回 000。
　　因此，我们可以使用 AND 门的输入解码，在计数器输出 5（十进制）计数后将其重置为零，从而得到所需的 MOD-5 计数器。当解码电路的输出为低电平时，它对计数序列没有影响。

　　模数 5 模计数器和真值表

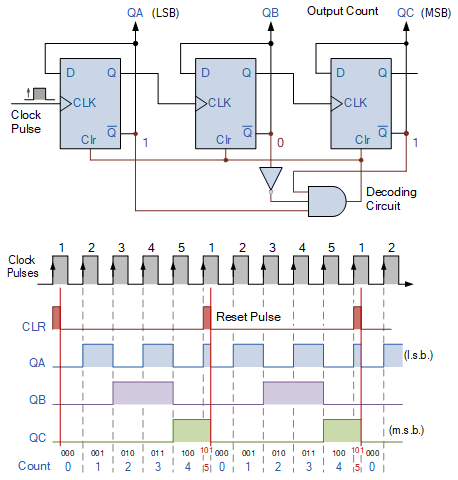
　　5模计数器电路
　　然后，我们可以围绕基本计数器使用组合逻辑解码电路（同步或异步）来产生我们需要的任何类型的 MOD 计数器，因为每个计数器的输出状态都可以解码以将计数器重置为所需的计数。
　　在我们上面的简单 MOD-5 示例中，我们使用了 3 输入与门来解码 101 二进制输出状态，但可以使用任何逻辑电路以所需计数重置触发器。
　　然而，使用异步计数器产生所需计数的任意大小的 MOD 计数器的缺点之一是，当计数器达到其复位条件时，可能会出现称为“毛刺”的不良影响。
　　在这短暂的时间内，计数器的输出可能会呈现不正确的值，因此有时使用同步计数器作为模数计数器，因为所有触发器都由相同的时钟信号计时，因此同时改变状态。
　　模数 10 计数器
　　十进制计数器是模数计数器电路的一个很好的例子，它使用外部组合电路来产生模数为 10 的计数器。十进制（除以 10）计数器（例如 TTL 74LS90）在其计数序列中有 10 个状态，使其适合需要数字显示的人机交互。
　　十进制计数器有四个输出，产生一个 4 位二进制数，通过使用外部 AND 和 OR 门，我们可以检测到第 9 个计数状态的发生，从而将计数器重置为零。与其他模数计数器一样，它逐个接收输入时钟脉冲，并反复从 0 计数到 9。
　　一旦达到计数 9（二进制为 1001），计数器就会返回到 0000，而不是继续到 1010。十进制计数器的基本电路可以由 JK 触发器（TTL 74LS73）制成，该触发器在时钟信号的负后沿切换状态，如图所示。

　　MOD-10 十进制计数器

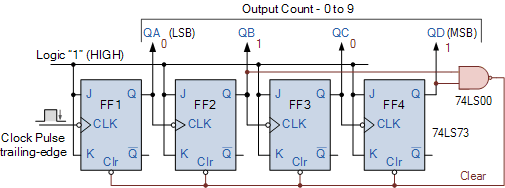
　　10 个十进制数计数器
　　MOD 计数器摘要
　　我们在本教程中关于MOD 计数器已经看到，二进制计数器是根据时钟信号生成二进制位序列的顺序电路，二进制计数器的状态由所有计数器输出形成的特定组合决定。
　　计数器可以产生的不同输出状态的数量称为计数器的模数或模数。计数器的模数（或 MOD 数）是计数器在一个完整计数周期内经过的状态总数，模 n 计数器也称为除以 n 的计数器。
　　计数器的模数为：2 n，其中 n = 触发器的数量。因此，3 触发器计数器的计数为 2 3 = 8 个计数状态，称为 MOD-8 计数器。计数器可以计数的二进制数为 2 n –1，计数为 (111) 2 = 2 3 –1 = 7 10。然后计数器从 0 计数到 7。
　　常见的 MOD 计数器包括 MOD 数为 2、4、8 和 16 的计数器，使用外部组合电路可以配置为计数到除 2 n模数以外的任何预定值。一般来说，可以使用“m”个触发器的任何排列来构建任何 MOD 计数器。
　　具有截断序列的计数器的常见模数是十 (1010)，称为 MOD-10。序列中具有十个状态的计数器称为十进制计数器。十进制计数器可用于连接数字显示器。其他 MOD 计数器包括 MOD-6 或 MOD-12 计数器，它们可用于数字时钟以显示一天中的时间。