这些假设之一称为虚拟短路，或简称为虚拟短路。实际上，这并不是理想运算放大器的基本特性之一。相反，虚拟短路是一种理论上的情况，由理想运算放大器的基本特征之一（即无限开环增益）引起。

　　假设我们有一个作为反相放大器连接的运算放大器。与运算放大器电路的情况几乎一样，其功能基于负反馈的使用。

　　获得该电路增益表达式的标准方法是假设同相输入端子 (V IN+ ) 处的电压等于反相端子 (V IN– ) 处的电压。由于同相输入端子接地，V IN+ = 0 V，因此 V IN– = 0 V。但为什么呢？为什么我们可以假设两个不同的电压是相同的？
　　无限增益

　　我们可以假设两个不同的电压是相同的，因为实际上这些电压之间的差异非常小，并且由于增益非常大，因此电压之间的差异非常小。考虑下面的图表和方程：

　　$$V_{OUT}=A\次(V_{IN+}-V_{IN-})$$
　　运算放大器是差分放大器。它通过对同相输入端子的电压与反相输入端子的电压之间的差应用开环增益（用 A 表示）来产生输出电压。如果我们重新排列该方程，以便将电压差与增益分开，我们将得到以下结果：
　　$$\frac{V_{OUT}}{A}=V_{IN+}-V_{IN-}$$
　　请注意，当开环增益增加时（对于给定的 V OUT）会发生什么：电压差减小。当增益接近无穷大时，电压差接近零。换句话说，如果增益无穷大，V IN+必须等于V IN–，这就是虚拟短路。
　　有限增益
　　不可能构建无限增益放大器并不会消除虚拟短路假设的实际价值。为什么？因为“虚拟短路”只是运算放大器的两个输入电压之间存在零差异的另一种说法，而在实际电路中，该差异“足够接近”为零。实际运算放大器的开环增益可以大于 100 dB。也就是说，产出与投入的比率至少为 100,000。假设我们有一个 A = 100 dB 的运算放大器，它产生 2.5 V 的输出电压。
　　$$V_{IN+}-V_{IN-}=\frac{2.5\ V}{100,000}=0.000025\ V$$
　　那是 25 V。当开环增益足够高以产生（非常）小的电压差时，虚拟短路作为实用的设计工具是可靠的，尽管事实上它是不现实的。事实上，这不仅不现实。这完全是自相矛盾的。
　　思考细节
　　零输入悖论

　　我不喜欢有人告诉我对 0 V 信号应用增益会产生 2.5 V 输出。我很久以前就知道零乘以零等于零。理想的运算放大器是差分放大器，其输入信号（即V IN+ –V IN–）为零。因此，理想的运算放大器在所有条件下都会产生零输出电压……这似乎不是一个非常有用的设备。

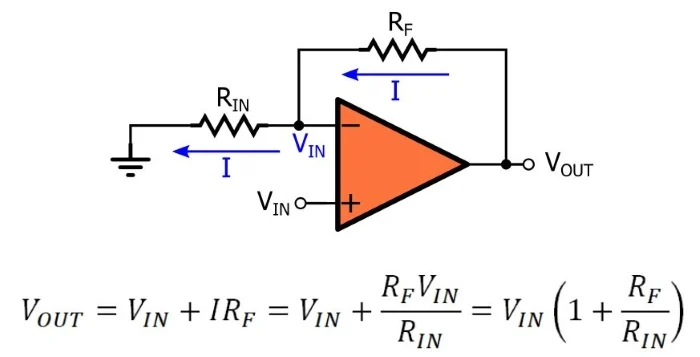
　　无法根据运算放大器的正常开环功能使用虚拟短路来确定 V OUT 。相反，虚拟短路是我们在负反馈环境下实现运算放大器时使用的一种工具。例如，当我们分析标准同相放大器时，虚拟短路假设（与零输入电流假设相结合）使我们能够推导出闭环增益的表达式，就好像运算放大器根本不存在一样。
　　当我看到这个电路时，我的大脑自然而然地忽略了三角形。运算放大器的增益 包含在虚拟空头假设中，除此之外，三角形就像投入溪流中的一块石头。电流只是绕着它流动。
　　输入是输入还是输出？
　　如果将运算放大器的反相输入端子接地并向同相输入端子施加 1 V 信号，则输出将在正电源轨处（或接近）饱和，并且 V IN+和 V IN–之间的差值为 1 V。这里没什么奇怪的；该器件的高开环增益将输出驱动至输出电压，并且输入电压保持在 1V。
　　然而，当我们开始谈论虚拟空头时，情况就不那么简单了。运算放大器似乎正在利用其高增益来强制输入电压符合要求。例如，在反相配置中，一个输入接地，另一个输入接收输入信号，但运算放大器随后决定这两个电压应该相同。这里究竟发生了什么？
　　同样，虚拟短路假设存在于负反馈放大器的背景下。在反相配置中，反相输入端子不仅连接到输入信号（通过电阻器），还连接到输出端子（通过电阻器）。输出电压影响反相输入端子的电压，运算放大器的增益影响输出电压，这导致我对虚拟短路的真正含义做出终陈述：
　　负反馈网络的存在建立了输入到输出/输出到输入的关系；
　　V IN+和 V IN–之间的差值必须与反馈网络施加的闭环增益一致；
　　因此，电路自然会产生反相和同相输入电压之间的差异非常小的情况，因为从极高增益差分放大器产生典型输出电压的方法是具有非常小的电压差。