一个有趣的应用电路，该电路由具有伪对数增益设置的 Dpot 控制放大器组成。但是，正如 Microchip 文本中所解释的那样，当电位器的控制设置接近 0 或 256 时，该电路实现的增益开始发生根本性变化。正如 Microchip 所说：“当电位器接近任一端子时，增益计算中的步长会急剧增加。建议将此电路用于 0.1 至 10 V/V 之间的增益。”
　　这是个好建议。不幸的是，遵循这个建议实际上会丢弃 256 个 8 位电位器设置中的 48 个，相当于损失了近 20% 的可用分辨率。图 1中所示的简单修改消除了这一限制。

　

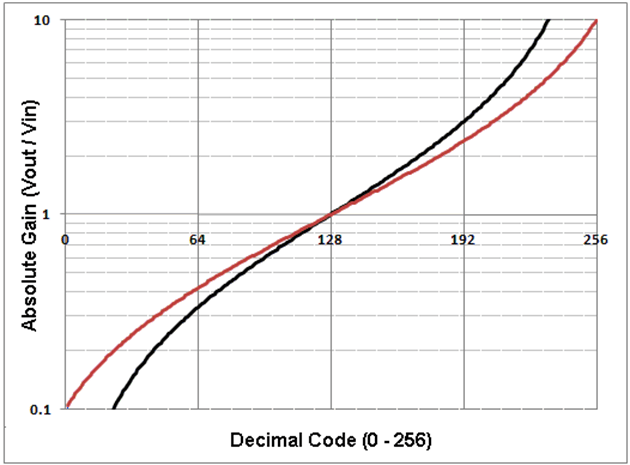
　　然而，尽管有了这种改进，关键项仍然是伪对数。它仍然不是真正的对数函数，事实上，从数量上看，它甚至没有那么接近对数函数，在某些地方偏差了近两倍。我们能做得更好吗？是的！
　　简单的（软件）技巧是准备一个 257 字节的对数查找表，将 0.1 到 10.0 的增益范围设置转换为对数生成这些增益所需的 Dpot 代码。
　　我们将表索引变量称为J 。然后，对于 (abs) 增益G从 0.1 到 10.0（含）的 257 字节表，
　　J(G) = (128 LOG 10 (abs(G)) + 128)
　　…例如…
　　J(0.1) = 0，
　　J(0.5) = 89，
　　J(1.0) = 128，
　　J(10.0) = 256，
　　等等。
　　检查图 1 中的增益表达式可知，（）增益G所需的Dpot 十进制代码N为：
　　N(G) = (284.4G – 28.4)/(G + 1)
　　…因此…
　　N(.1) = (28.4 – 28.4)/(.1 + 1) = 0/1.1 = 0，
　　N(.5) = (142 – 28.4)/(.5 + 1) = 114/1.5 = 76，
　　N(1.0) = (284.4 – 28.4)/(1 + 1) = (256)/2 = 128，
　　N(10.0) = (2844 – 28.4)/(10 + 1) = 2816/11 = 256，

　　等等。

　　图3总结了G、J和N之间的终关系。
　　图 3 Dpot 设置 [N(J)] 与对数表索引 [J(G)]，总结了 G、J 和 N 之间的关系。
　　对数增益表可在此 Excel 表中找到。终结果（具有 8 位允许的尽可能好的对数一致性）如图4中可爱的绿线所示。
　　图 4增益[G abs = 10 (J/128 -1) ] 与十进制码 (J) 的关系。