在一些技术文章中,转换器的操作是在理想条件下进行研究的。理想条件是没有中断、干扰和错误导致操作偏离正常条件。这些不可避免的偏离正常条件的中断可能是由于电路参数的变化造成的,例如电源和负载的电压、
开关时间以及电感器或
电容器等电路元件。系统的这种行为称为动态系统行为,需要通过控制机制进行纠正才能获得正确的输出。这需要通过建模方法分析和设计控制器,这为我们提供了广泛的范围来分析各种中断或问题。 控制系统通过开环或闭环系统测量扰动来控制电路参数。如图所示,开环控制器可以通过前馈路径化预期的扰动。然而,单靠开环系统无法满足转换动态控制的需要。在这里,闭环系统可用于测量系统的当前行为并通过反馈采取适当的措施。控制系统的配置如下图 1 所示。

控制系统总体配置
图 1. 控制系统的总体配置
在设计所需操作模式的组件时,需要了解转换器的静态和动态行为。开关转换器是一个随时间变化、非线性和离散的系统,因此必须使系统对线路中的负载或干扰不那么敏感。
闭环控制器通过注意输入的偏差并改变触发角等参数来设置输出。闭环的优点是,控制器还可以控制输出切换期间出现的瞬态。前馈路径本身无法设置输出的期望值,并且会产生超出允许限度的瞬态。
维持输出电压或电流的解决方案之一是使用 PI 或 PID 控制器。当涉及到稳态误差时,由于包含微分误差/输出,PID 控制器比 PI 控制器更快。
在本技术文章中,说明了获得适合非线性和线性转换器模型的技术。为简单起见,转换器模型将针对连续或不连续传导模式设为线性。因此,特别关注线性时不变 (LTI) 模型。线性模型用于创建等效电路。
基本 AC 建模方法
需要为不同阶段选择合适的模型。例如,闭环控制器对于特定阶段的电路开环性能来说并不是一个好的选择。有不同的方法来设计转换器的模型。在这里,我们可以从电路平均设计模型开始讨论,该模型描述了转换器的平均性能以供分析,但它并不总是的方法。有时,电路方法或平均方法并不总是适合和方便建模控制器,因此我们还将看到状态空间建模方法。
通过电路平均法建立动态模型
高频转换器使用简单的电路图。我们将构建非线性模型并将其转换为描述电路小信号性能的线性电路。
功率转换器的开关操作会导致组件中电流和电压产生脉冲频率。但为了实现稳定性,很难考虑这些电压和电流的脉冲频率。对于转换器的动态分析,需要采取另一种方法,然后寻找详细的开关模式行为或脉冲频率的脉动,从而产生动态平均法。
在许多电力
电子应用中,电流和电压的平均值比瞬时值更有价值,前提是谐波和波纹的值足够小,可以忽略不计。因此,我们可以使用电路方法取电压或电流等变量的平均值。任何时间的平均值都是在间隔 T 内取的,间隔 T 是与电源电路过程相关的短重复开关间隔。
ˉˉˉˉˉˉˉˉˉx(t)=1T∫tata?Tx(t
对长度 T 取平均值。因此,ˉˉˉˉˉˉˉˉˉx(t) 与 x (t) 相比更平坦。
如果 x(t) 具有特定频率 fC=cT 的振荡。那么,这些频率分量在动态平均过程中将被抵消。
这些平均变量也满足基本方程,即 KCL 和 KVL。
因此,我们可以说
ˉˉˉˉˉˉˉˉˉˉˉˉˉVR(t)=RˉˉˉˉˉˉˉˉˉˉˉˉIR(t)
ˉˉˉˉˉˉˉˉˉˉˉˉVL(t)=LddtˉˉˉˉˉˉˉˉˉˉˉIL(t)
应用平均和微分的顺序是可以互换的(即,可以先应用任何方法,然后再应用其他方法)。
同样,对于电容器,我们有以下方程:
CddtˉˉˉˉˉˉˉˉˉˉˉˉˉVC(t)=ˉˉˉˉˉˉˉˉˉˉˉˉIC(t)
利用这些类型的基本方程,我们可以创建一个平均电路模型。
我们必须用平均值改变所有瞬时值,而不改变 LTI 组件。电路的线性部分不会改变,因为它们对正常变量和偏差变量施加了相同的约束。但是,时变组件和非线性组件会随着具有某个平均电压或平均电流值的等效电路的表示而改变。例如,BJT 开关被替换为小信号模型,如下所示: BJT 的非线性模型和小信号模型
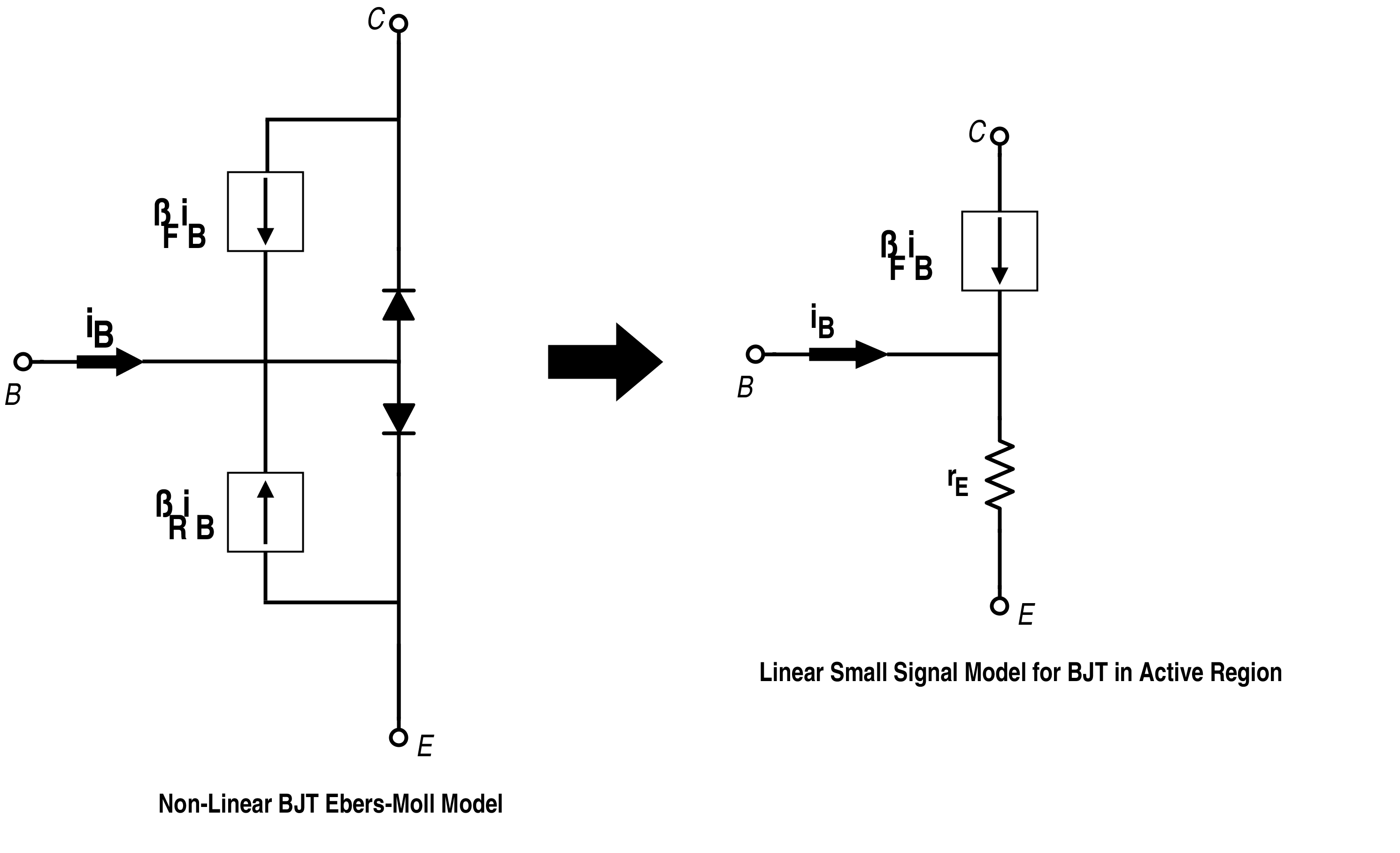
图 2. BJT 的非线性模型和小信号模型
线性模型又称为小信号模型,它通过使非线性电路近似线性来简化分析判断。我们还可以分析正常工作条件下偏差较小的稳定性。因此,控制设计的初始目标是使线性模型比非线性模型更稳定,因为非线性模型可能会变得繁琐。
考虑一个电压源和一个由等效诺顿电路表示的电路,其中转换器位于中间,如图 3 所示。 通用开关电路

图3.通用开关电路
这里,x (t) 是一个开关函数,它对源电压进行调制。这取决于开关的占空比。q(t) 的值设置在有限值之间,例如降压转换器的 1 和 0 之间,PWM 逆变器的 1、0、-1 之间。此基本开关电路的平均电路如图 4 所示。 上述电路的平均电路
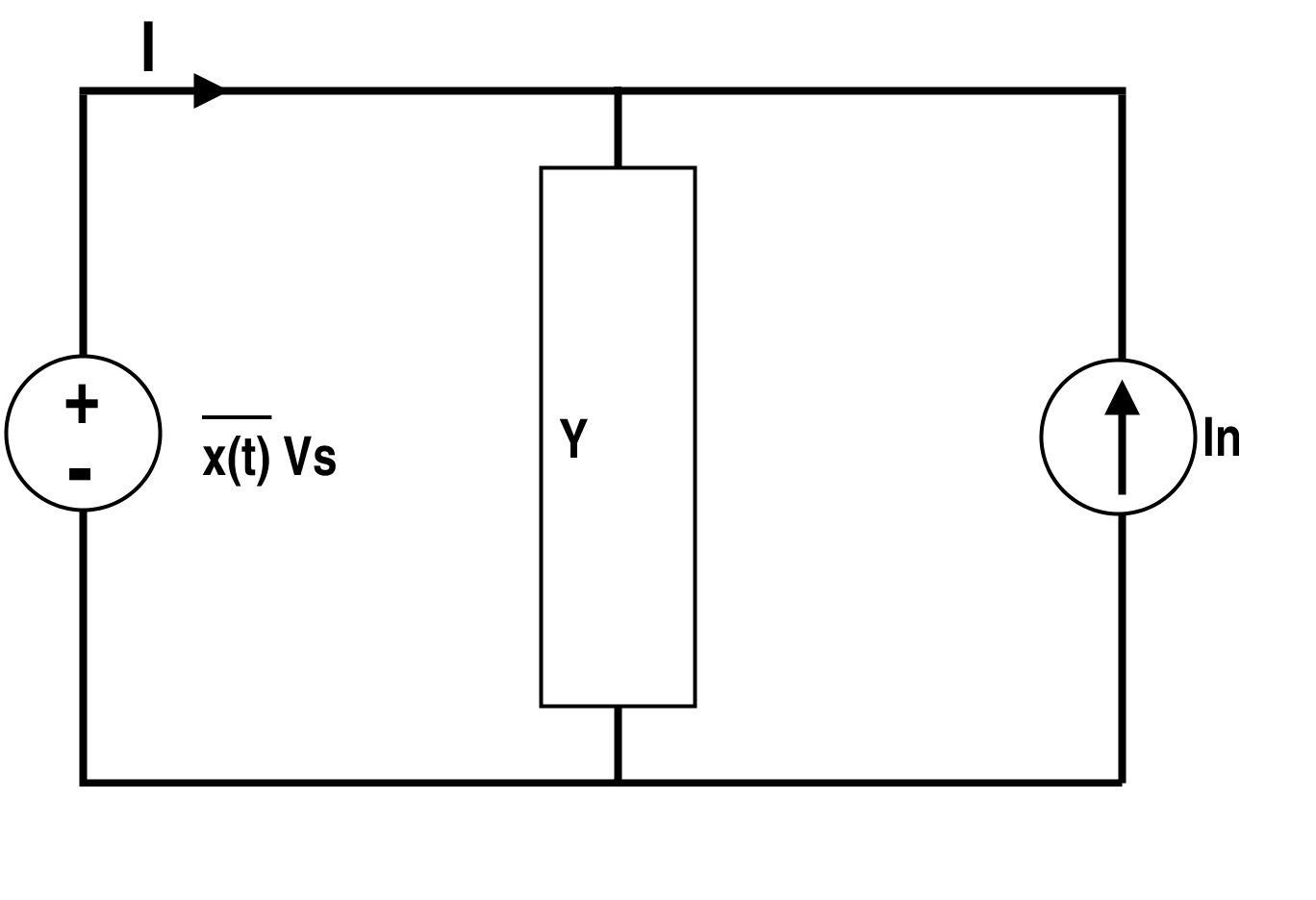
图 4. 上述电路的平均电路
函数
是一个平均开关函数,也称为连续占空比。
完全取决于控制变量和电流平均值,即 = ˉˉˉˉˉˉˉˉˉx(t)VS
这是借助比较器、锁存器、时钟等电路生成的。开关函数位于锁存器的输出端。锁存器连接到时钟和比较器的输出。控制器的输出是调制的占空比连续平均值波,连接到比较器。时钟可以是施加到比较器正极的锯齿波形。
与输入电压成反比。因此,输入电压变化引起的输出扰动在平均电路中受到限制。输入电压的前馈控制减少了瞬态和稳态误差对输出的影响。
随时间变化,甚至可以为负。但是,如果 x(t) 的周期为 T,且开关频率没有任何偏差,则
用线性小信号模型代替开关,可以为我们控制模型性能的变量。图 5 显示了开关的标准电路,可以用图 6 中的连续导通平均电路代替。平均电路也可以用理想
变压器表示,如图 7 所示。 标准开关电路
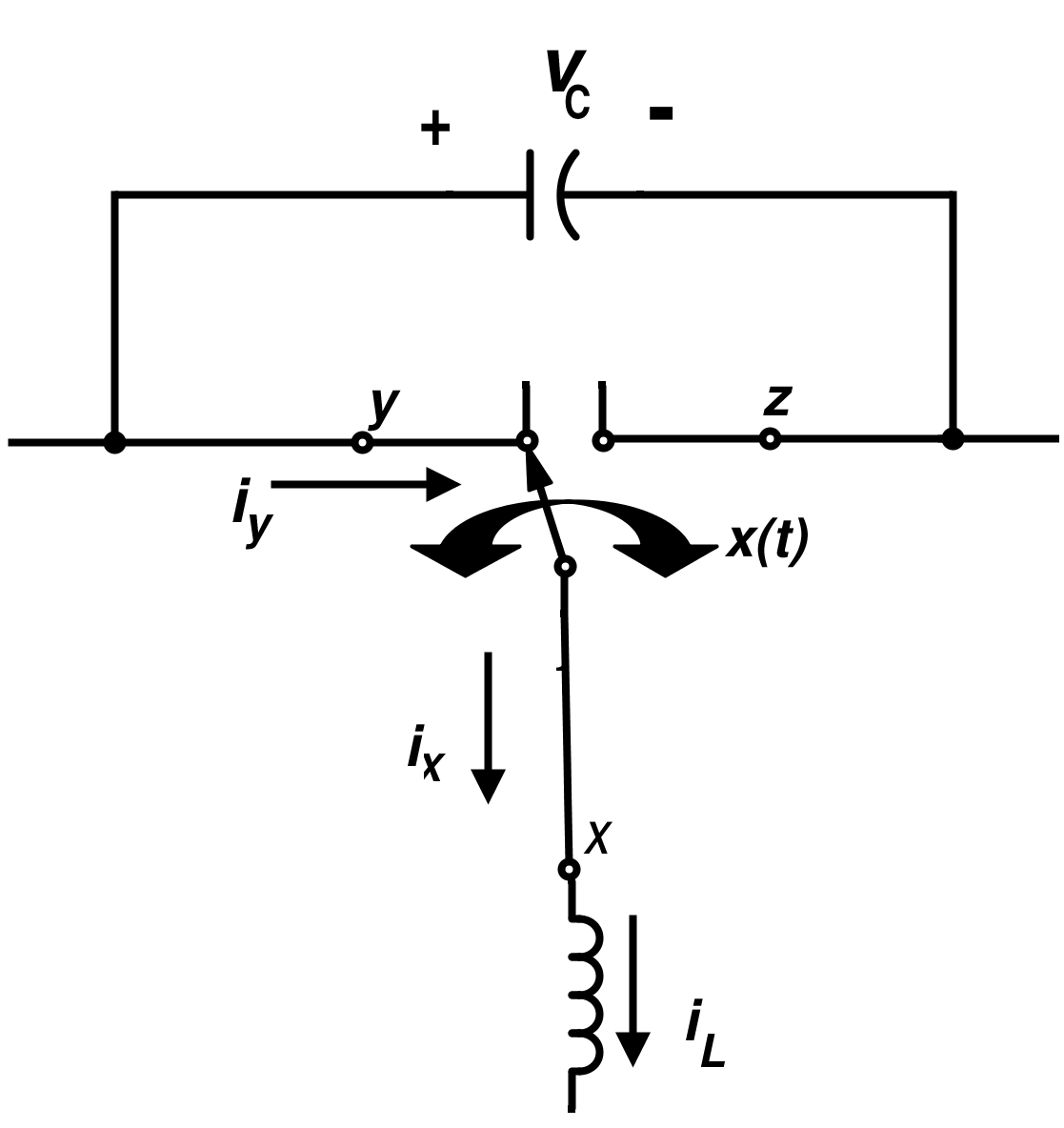
图 5. 标准开关电路
假设只有很小的纹波,那么负载电流和电容电压可以用它们的平均值很好地近似。此外,假设负载电压、电源电压和电容电压在长度 T 的间隔内变化不大。
如果我们假设 iX ( t) 由于波动较小且平均值在周期 T 内变化缓慢而接近恒定,则
对于区间 tT ≤ r ≤ T,
现在,电感电压平衡条件和电容电荷平衡条件不成立。但对于标称值来说,这是正确的。此外,这些方程表明存在一个单独的电压和电流源来表示偏差。 连续导通模式下标准开关的平均电路
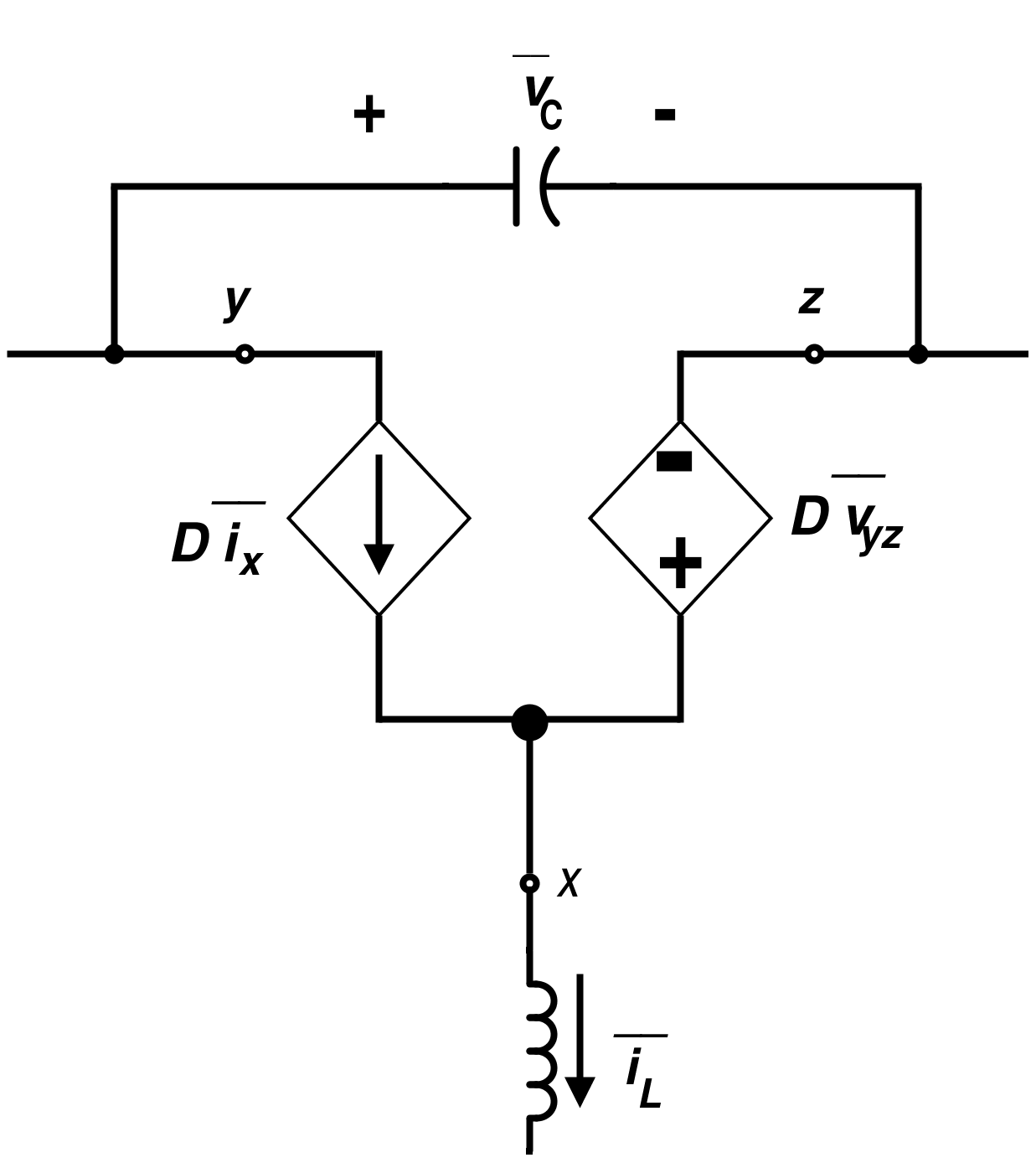
图 6. 连续导通模式下标准开关的平均电路 使用理想变压器的标准开关平均电路

图 7. 使用理想变压器的标准开关平均电路
我们可以进一步简化该电路以实现线性化。
假设电路初处于稳定状态,平均值和瞬时值相等,例如
,其中 V n (t) 是正常工作电压。现在,如果与正常情况有任何微小偏差。那么非线性电路中的每个电压都被替换为两组电压或电流以解释偏差。系统对原始变量和偏差施加约束。
由于小信号假设,我们现在有,
其中V n (t)为正常工作电压,无任何偏差。
使用这些方程(包括偏差)来求解电感和电容,我们将得到模型的非线性项。这些方程需要使用泰勒级数展开。如果我们保留一阶项,我们将得到线性模型,该模型也适用于小偏差。 标准开关的线性平均模型
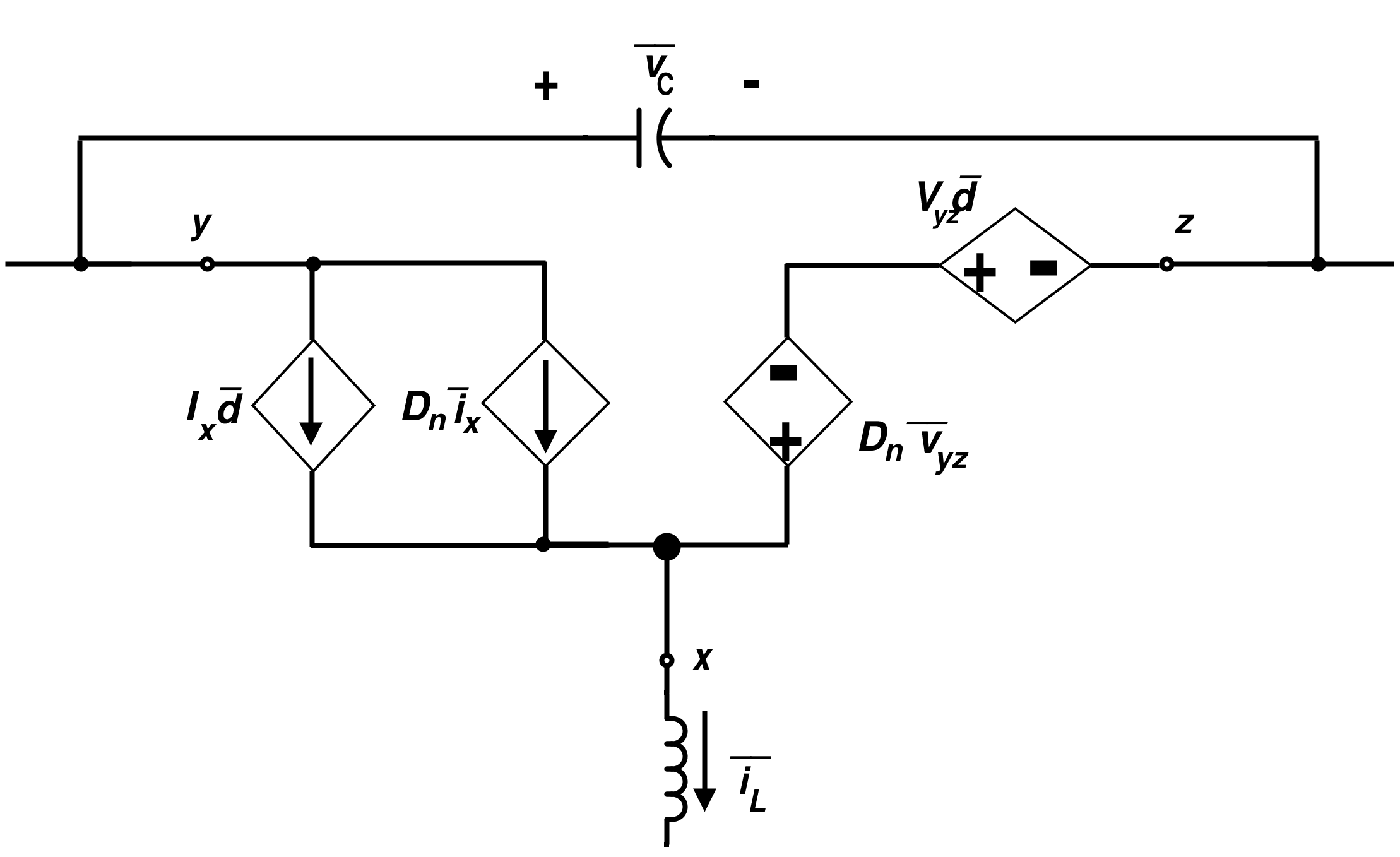
图 8. 标准开关的线性平均模型 图9显示了使用理想变压器的开关线性模型的另一种表示形式。
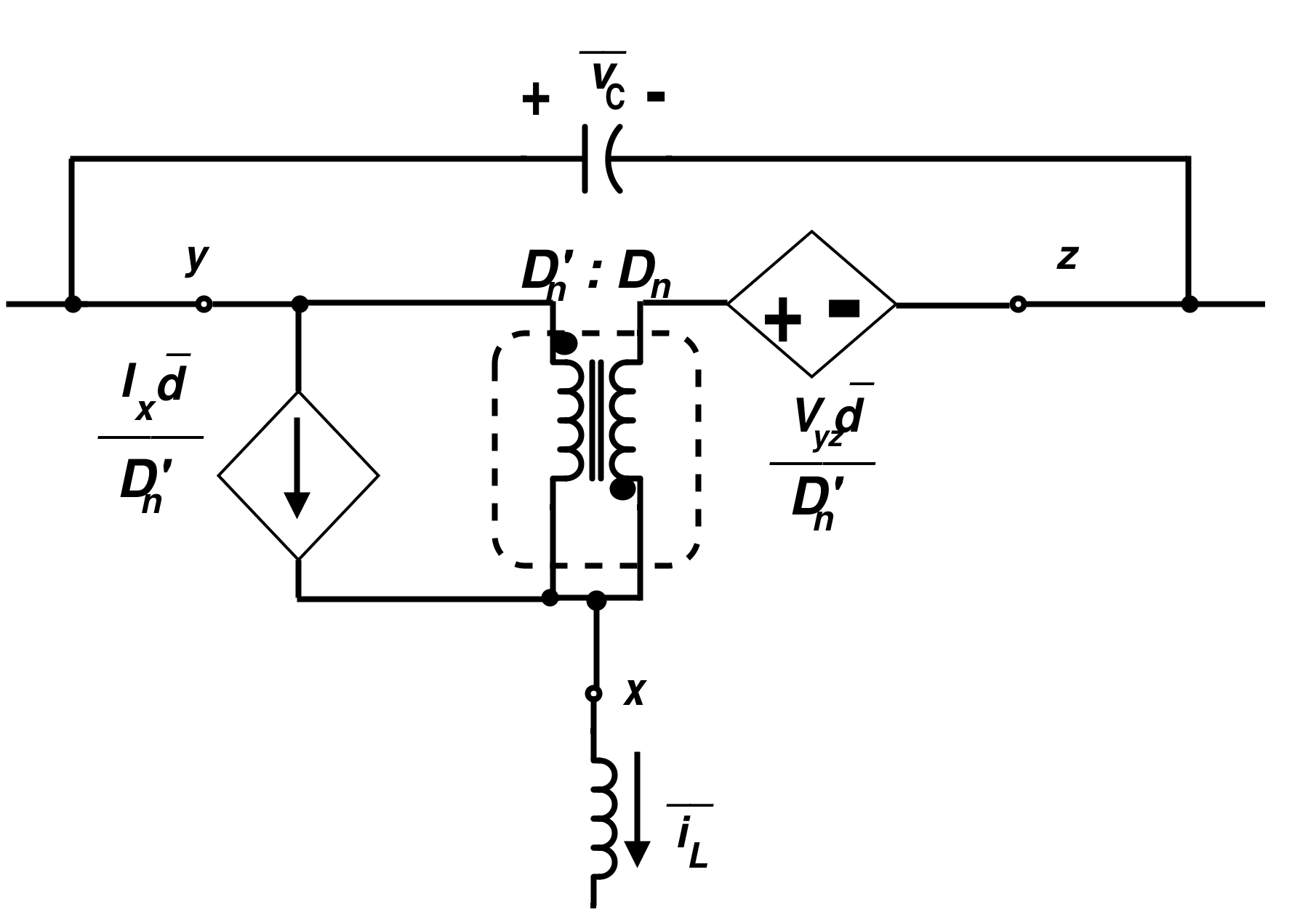
使用理想变压器的开关线性模型 图 9. 使用理想变压器的开关线性模型
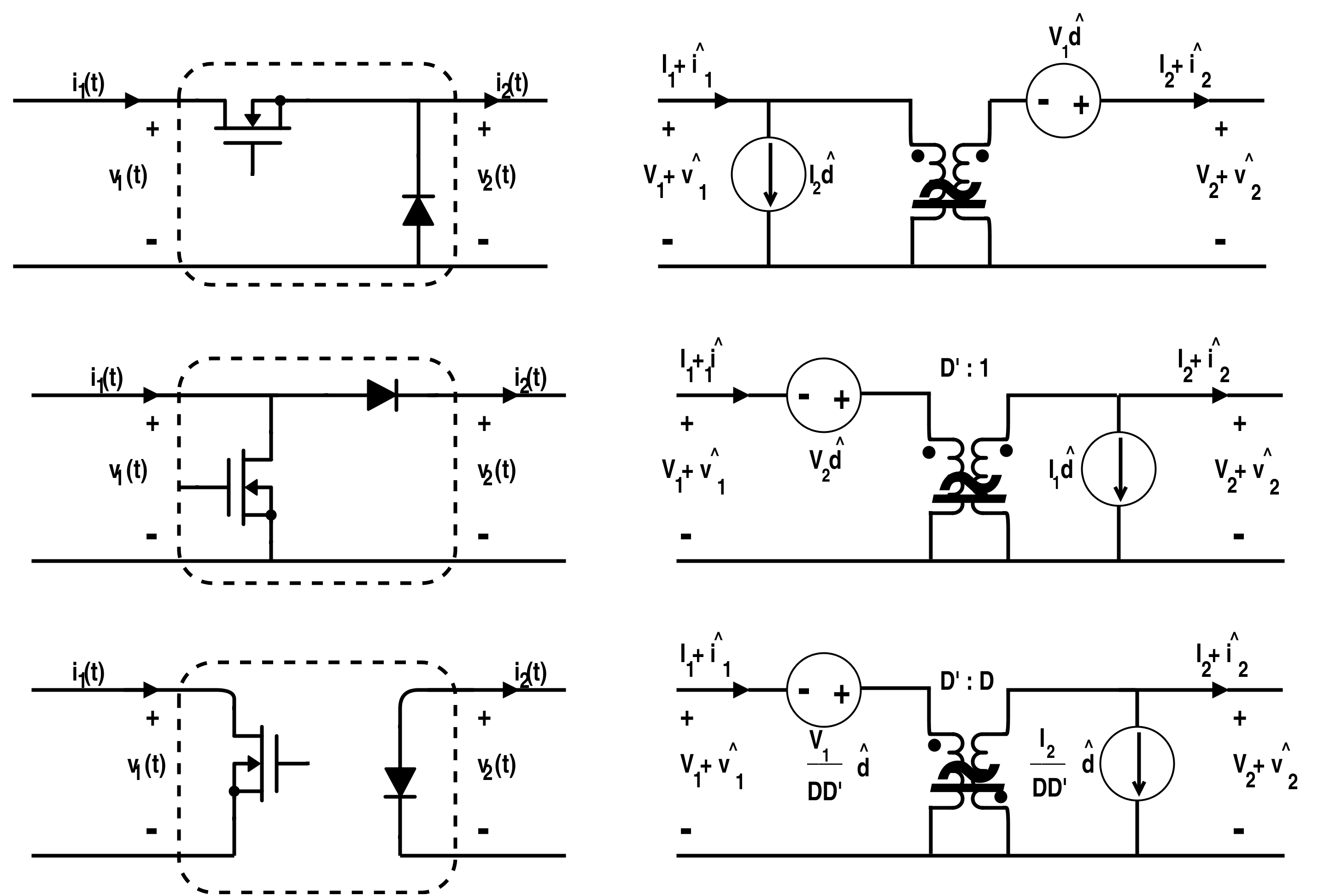
图 10 显示了三种不同开关连接模式的配置。这些线性模型对交流和直流均有效。
不同的开关配置及其线性模型转换
图 10. 不同开关配置及其线性模型转换
下面显示的线性电路甚至可以设计为不连续传导模式。当不连续传导负载 R 足够高时,电感电流的值达到零值。如果输入电压在开关周期内保持不变,则电感电流线性上升,直到衰减为零。当电流衰减为零时,它可以形成 RLC 振铃电路,该电路由线性段近似。降压转换器的不同电路模式如下所示。振铃电路如图 11(b) 所示,需要近似线性。 不连续传导模式的不同电路图
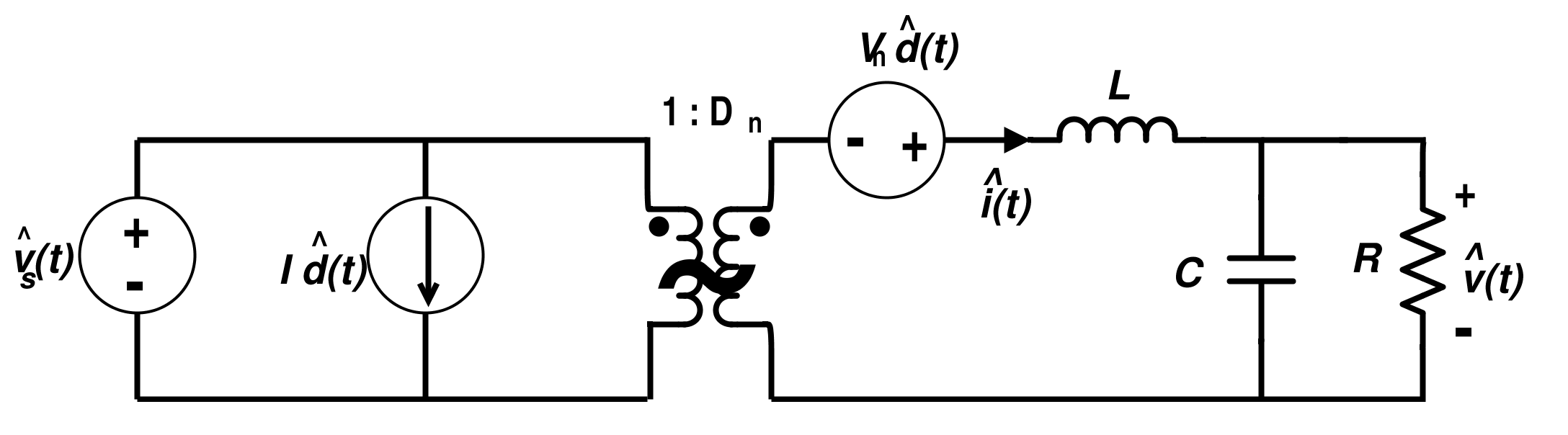
图 11. 非连续传导模式的不同电路图
几个基本转换器的结果
现在,图 12 至图 19 给出了降压转换器、升压转换器、升降压转换器和反激式转换器的线性电路模型和开关转换器电路。 降压转换器的开关转换电路
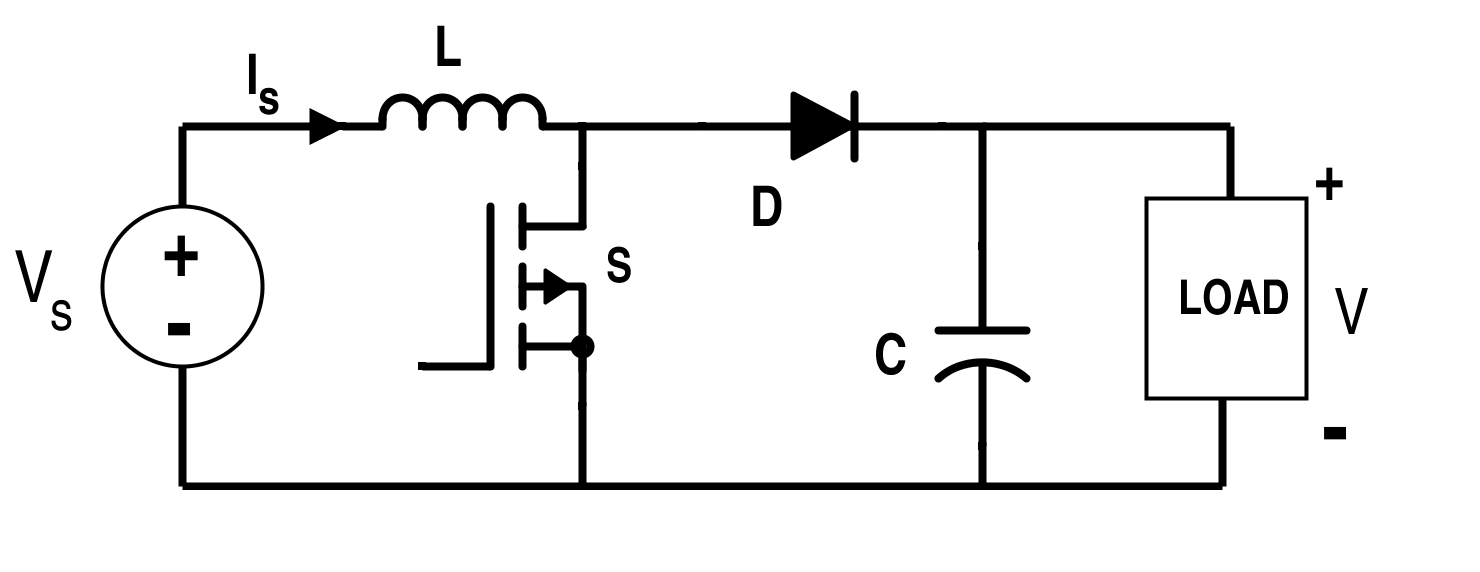
图 12. 降压转换器的开关转换器电路
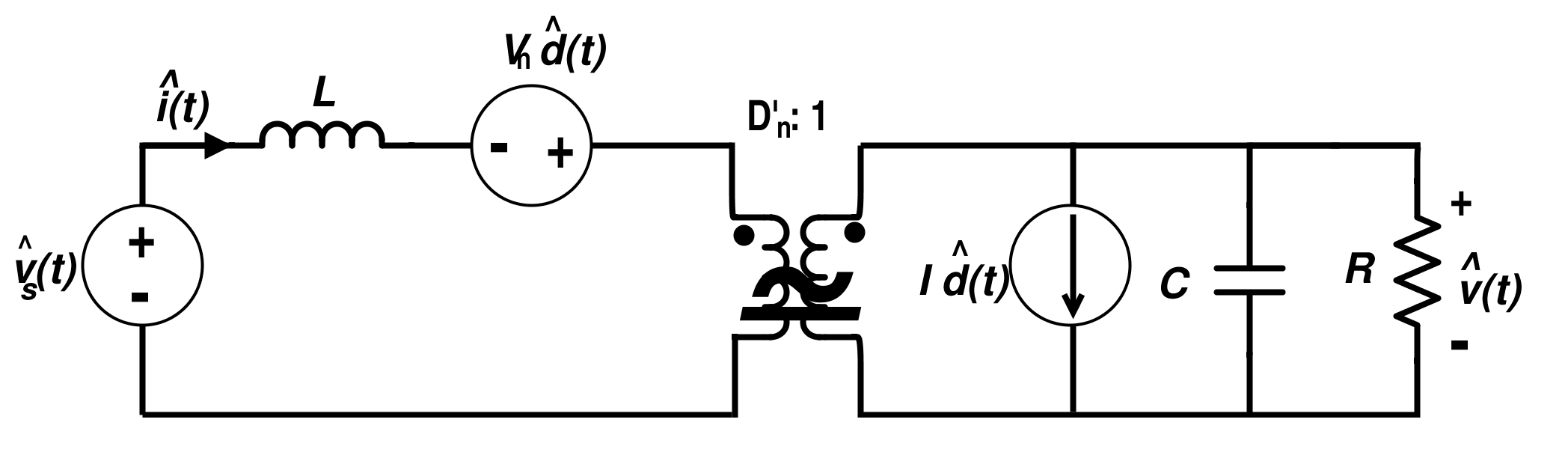
图 13. 降压转换器的线性电路模型
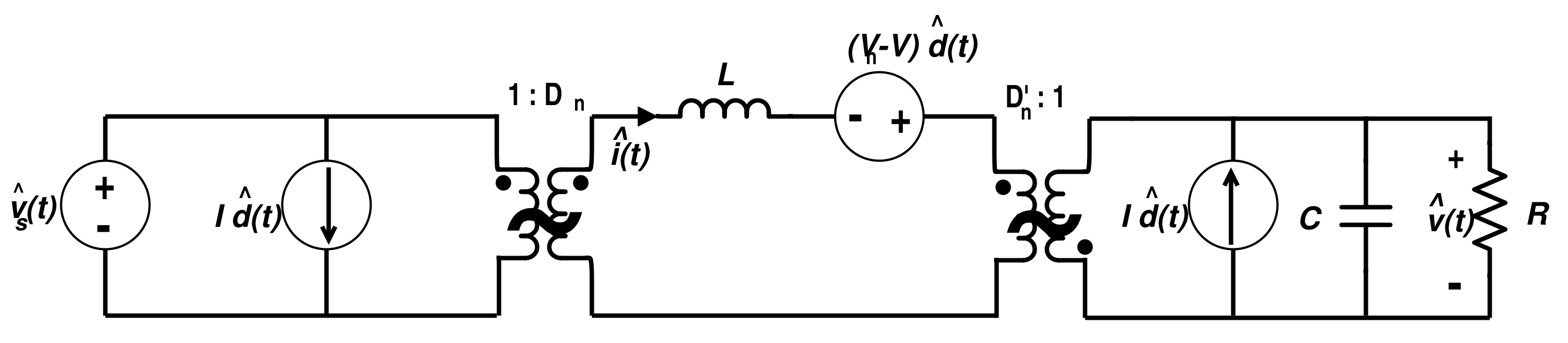
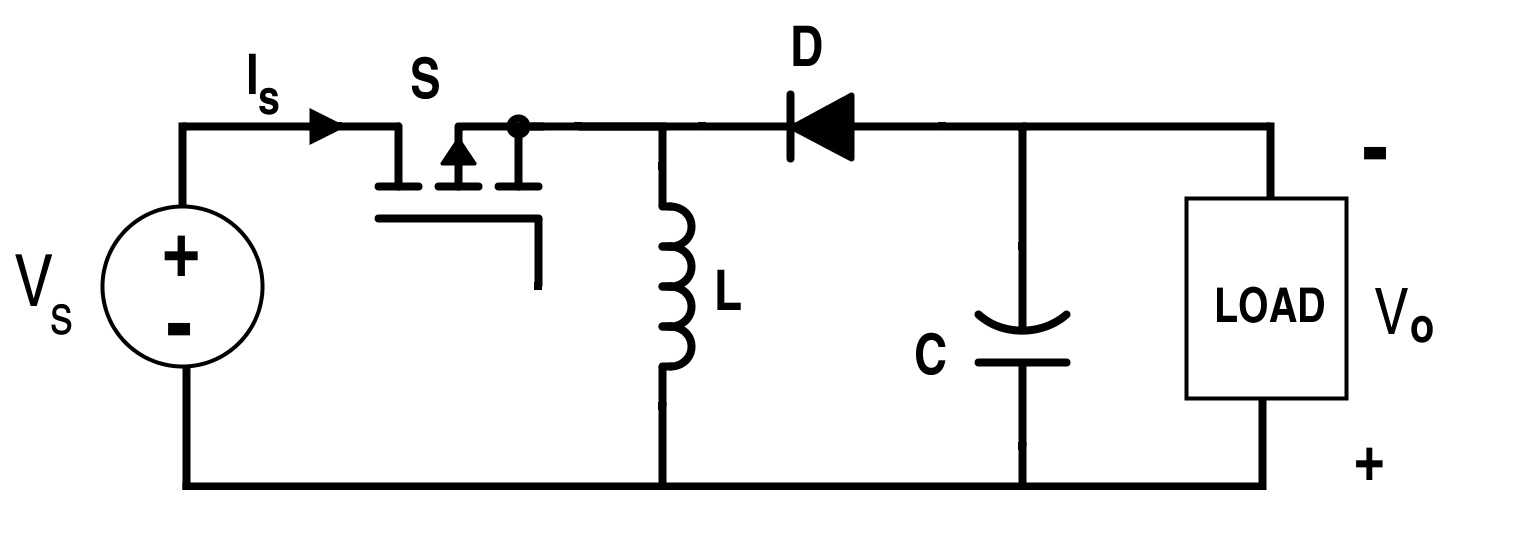
图 14. 升压转换器的开关转换器电路
降压-升压转换器的线性电路模型

图 17. 降压-升压转换器的线性电路模型 反激式转换器的开关电路
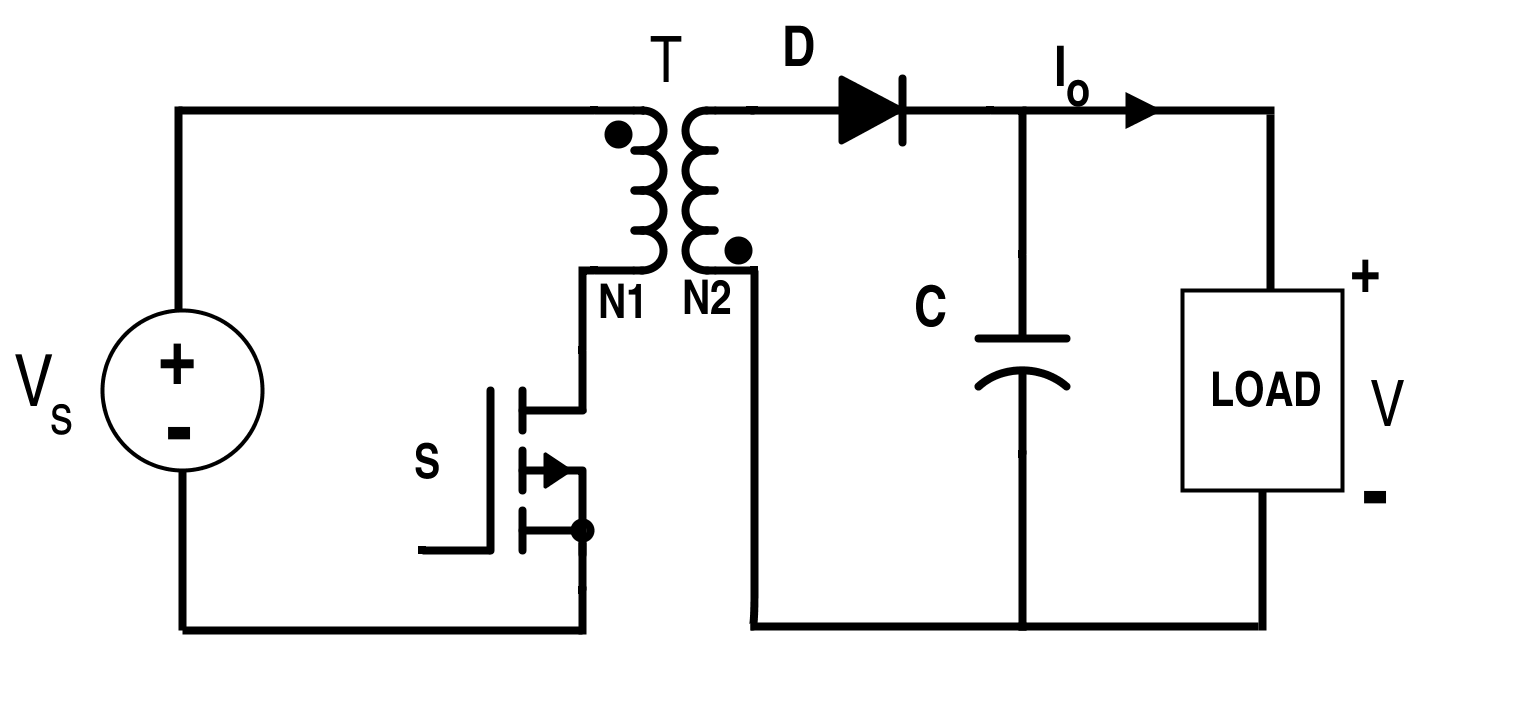
图 18.反激式转换器的开关电路
设开关S导通时的电阻为R ON ,
开关S与
二极管D交替导通。 反激式转换器的线性电路模型
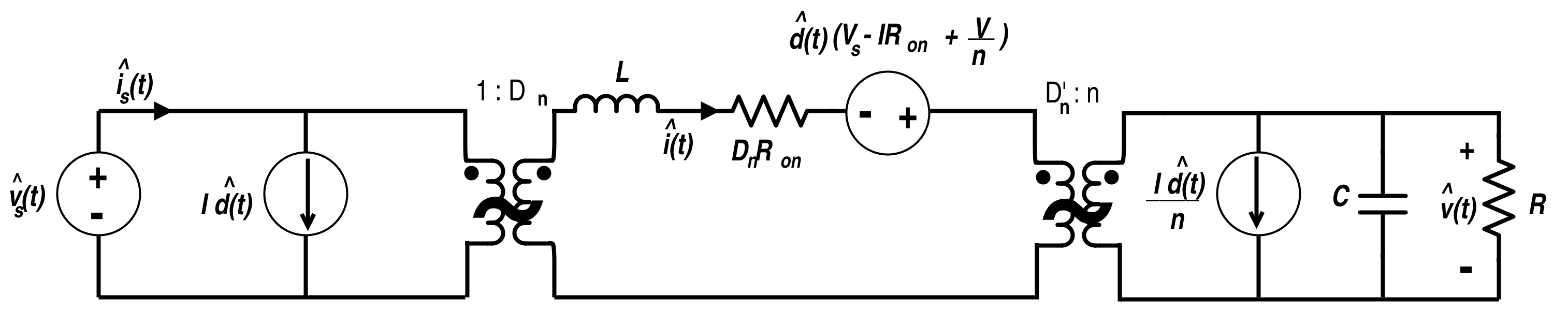
图 19.反激式转换器的线性电路模型














 降压-升压转换器的线性电路模型
降压-升压转换器的线性电路模型

