三角波发生器 (TWG) 的另一种变体是使发生器环路成为差动环路,如下所示。这是 Exar 2206 FG IC 的简化电路。
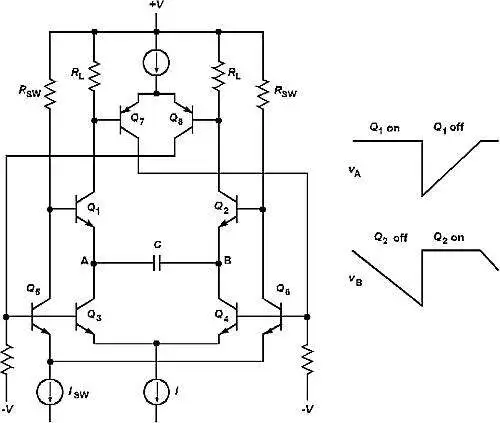
在该电路中,定时
电容器C不接地,而是以差分方式悬空在电流源
开关之间。为了保持准确的波形,环路后面的差分放大器必须能够将两个波形片段重建为连续(“无故障”)波形。HP3314A 中还使用了性能更高的差分 TWG。
自对称 FG
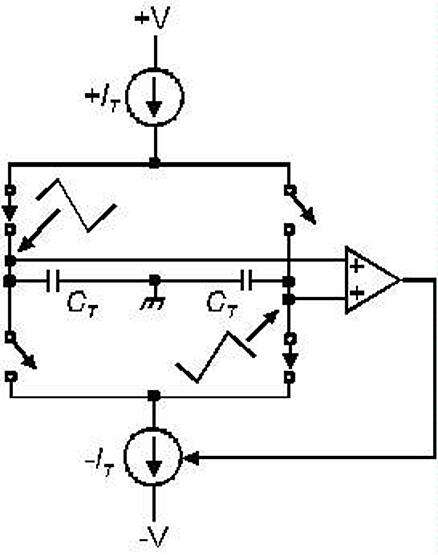
差分波形生成的优势在 Tek FG506 原型(从未作为产品推出)中得以实现,如下图所示。通过检测差分波形的总和并将其放大为差分误差,可以校正两个定时电容器的值差异。然后,由误差驱动 – I T 电流源,以保持波形对称。
这种自动对称方案能够在四十个十年的频率扫描中保持对称性,而以前的方案基本上无法实现这一壮举。不对称是正弦失真的主要原因,FG506 采用了四十个十年的正弦扫描。
下图所示的 FG506 框图说明了具有自对称性的扫描 FG 所涉及的内容。
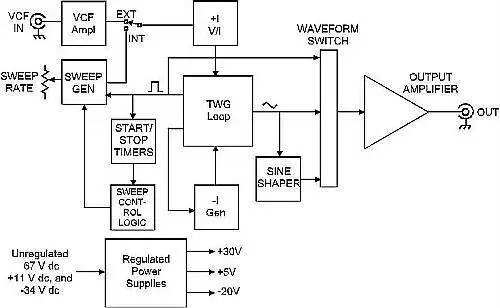
如下所示,另一个亮点是生成指数扫描频率(由“扫描生成”块生成),这样,通过使用四十倍频正弦波(10 Hz 至 100 kHz)扫描音频放大器或其他被测设备,可以通过观察屏幕上的正弦波幅度在示波器屏幕上显示波特幅值图。指数扫描使水平示波器轴显示为对数轴。如今,有了微控制器,这种简单的技术仍然适用,因为 FG 频率通常超过 μC 中断率。
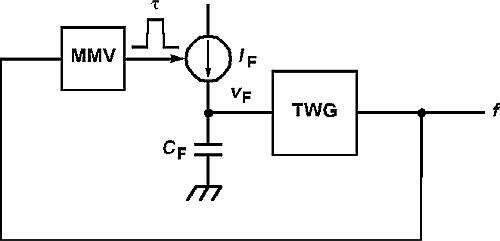
三角波发生器的压控频率 (VCF) 输入v F 是积分电流脉冲I F ,持续时间为τ T ,其中T = 1/ f 。因此 ,当 TWG 输出的每个周期触发单稳态 (MMV) 时,固定电荷会转储到C F 中。因此, v F 每个周期 增加 Δ v F ;
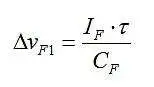
在 Δ t间隔内,vF ( t ) 的变化率为
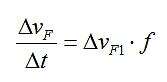
对于频率扫描期间的许多周期n,速率可以用导数来近似;
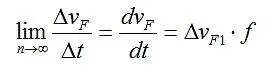
TWG 输出频率f取决于v F , 其比例因子为K F ,并且
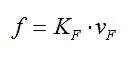
然后结合方程,
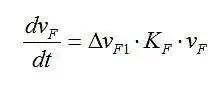
这个一阶微分方程的解为,
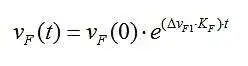
频率因此呈指数变化:
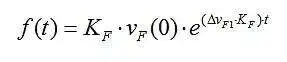
在基于 μC 的 FG 中,可以使用相同的基本原理通过避免指数函数的计算来简化指数的软件生成。相反,它来自增量函数生成。在低 FG 频率下,对于每个 FG 周期,μC 都会中断,并且v F 会以决定频率扫描速率的量递增。FG 频率很容易超过快速 μC 可以处理的频率,因此 FG 频率会输入到 μC 计数器中,通过该计数器可以测量频率并控制v F。 在扫描期间,计数器设置为每N 个 周期溢出,从而导致中断,其中 应用Δ v F。N 取决于扫描的低频和高频限制。然而,对于宽带扫描,模拟电路仍然可行,也许是,以保持 μC 中的N = 1,以便在更短的时间内扫描低频。1 Hz 的低频可能导致扫描持续数秒。
附加 FG 功能
正弦整形器
除了输出三角波和方波的基本 TWG 环路之外,正弦波也是 FG 功能的一部分。与上述 FG 电路一样,
二极管电阻网络在 FG 历史早期用作分段线性函数整形器。每个整形器的多个钳位电路之一如下所示。
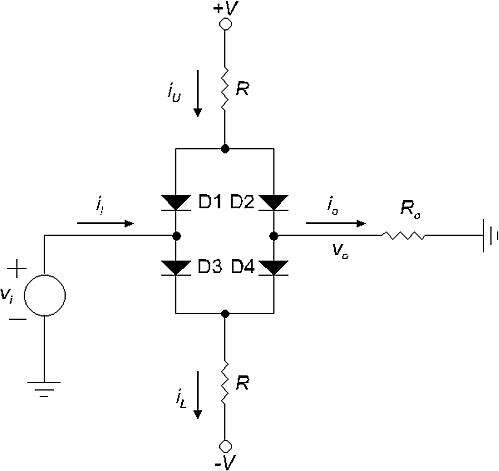
通常,三到四个这样的电路并联,并使用一个公共输出电阻,该电阻位于 各段的
分流器R o 和地之间。通过用R调整断点并用R调整 斜率,音频频率下的总谐波失真 (THD) 通常可以降低到 0.1% 左右。
通过使用跨线性电路,可以进一步降低该值,并在较高频率下保持较低值。跨线性电路基于 BJT 结的匹配以及 使用它们生成幂级数函数的能力。例如,下面显示的电路实现了两个象限的正弦函数的三项泰勒级数展开。发射极耦合 BJT 对电流源是正弦级数系数的比率。
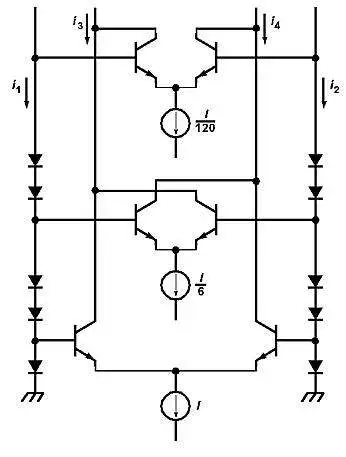
下面显示了一个改进和简化的四象限正弦波发生器。它由差分三角波电流驱动,输出为差分正弦波。它由 Art Metz 开发,Tektronix 拥有一项已过期的。
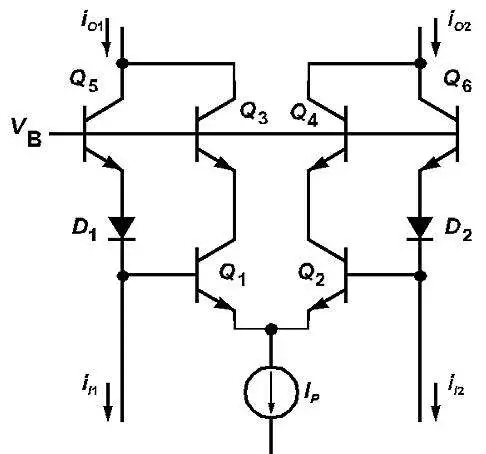
利用该电路可以实现远低于 0.1% 的 THD 值。
幅度、频率、对称性和门控的控制
由于 FG 电路的多功能性,用户可以控制多个波形参数。除了电压控制频率 (VCF) 输入之外,乘法器还提供幅度控制,用于对波形进行幅度调制。两个定时电流源允许对每个半周期进行独立控制。在某些 FG 中,对称性可以通过输入电压来改变,但在许多 FG 中,波形选择功能提供了一些固定的对称性 - 通常是 10% 和 90% 的值,可产生斜坡、反向斜坡和脉冲。具有不对称半周期的正弦波也是 FG 电路的副作用,尽管它们很少作为用户选择提供;它们作为波形的实用性令人怀疑,尽管它们确实出现在一些数字相位调制技术中。
有用的是通过外部电压输入来选通波形。波形被打开和关闭。更有用的是 FG 波形的相位选通。Tek FG501 有一个控件,可以调整起始相位。在另一种变体中, 可以同步选通和计数N 个周期以生成N 个周期的突发脉冲。
输出的表现形式可能因驱动它的
功率放大器而异。标准输出电阻为 50 Ω。幅度范围从快速发生器的 5 V 到多功能发生器的 +/- 20 V。输出偏移控制增加了多功能性。FG 与 PG 的不同之处在于,幅度和偏移必须交互变化才能设置所需的高低脉冲或峰值和谷值。但是, Fgs 中的幅度处理 与 PG 中的幅度处理没有任何不同。
 在该电路中,定时电容器C不接地,而是以差分方式悬空在电流源开关之间。为了保持准确的波形,环路后面的差分放大器必须能够将两个波形片段重建为连续(“无故障”)波形。HP3314A 中还使用了性能更高的差分 TWG。
在该电路中,定时电容器C不接地,而是以差分方式悬空在电流源开关之间。为了保持准确的波形,环路后面的差分放大器必须能够将两个波形片段重建为连续(“无故障”)波形。HP3314A 中还使用了性能更高的差分 TWG。 下图所示的 FG506 框图说明了具有自对称性的扫描 FG 所涉及的内容。
下图所示的 FG506 框图说明了具有自对称性的扫描 FG 所涉及的内容。

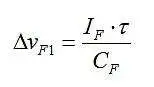 在 Δ t间隔内,vF ( t ) 的变化率为
在 Δ t间隔内,vF ( t ) 的变化率为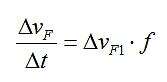
 TWG 输出频率f取决于v F , 其比例因子为K F ,并且
TWG 输出频率f取决于v F , 其比例因子为K F ,并且
 这个一阶微分方程的解为,
这个一阶微分方程的解为, 频率因此呈指数变化:
频率因此呈指数变化: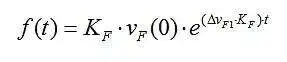 在基于 μC 的 FG 中,可以使用相同的基本原理通过避免指数函数的计算来简化指数的软件生成。相反,它来自增量函数生成。在低 FG 频率下,对于每个 FG 周期,μC 都会中断,并且v F 会以决定频率扫描速率的量递增。FG 频率很容易超过快速 μC 可以处理的频率,因此 FG 频率会输入到 μC 计数器中,通过该计数器可以测量频率并控制v F。 在扫描期间,计数器设置为每N 个 周期溢出,从而导致中断,其中 应用Δ v F。N 取决于扫描的低频和高频限制。然而,对于宽带扫描,模拟电路仍然可行,也许是,以保持 μC 中的N = 1,以便在更短的时间内扫描低频。1 Hz 的低频可能导致扫描持续数秒。
在基于 μC 的 FG 中,可以使用相同的基本原理通过避免指数函数的计算来简化指数的软件生成。相反,它来自增量函数生成。在低 FG 频率下,对于每个 FG 周期,μC 都会中断,并且v F 会以决定频率扫描速率的量递增。FG 频率很容易超过快速 μC 可以处理的频率,因此 FG 频率会输入到 μC 计数器中,通过该计数器可以测量频率并控制v F。 在扫描期间,计数器设置为每N 个 周期溢出,从而导致中断,其中 应用Δ v F。N 取决于扫描的低频和高频限制。然而,对于宽带扫描,模拟电路仍然可行,也许是,以保持 μC 中的N = 1,以便在更短的时间内扫描低频。1 Hz 的低频可能导致扫描持续数秒。 通常,三到四个这样的电路并联,并使用一个公共输出电阻,该电阻位于 各段的分流器R o 和地之间。通过用R调整断点并用R调整 斜率,音频频率下的总谐波失真 (THD) 通常可以降低到 0.1% 左右。
通常,三到四个这样的电路并联,并使用一个公共输出电阻,该电阻位于 各段的分流器R o 和地之间。通过用R调整断点并用R调整 斜率,音频频率下的总谐波失真 (THD) 通常可以降低到 0.1% 左右。 下面显示了一个改进和简化的四象限正弦波发生器。它由差分三角波电流驱动,输出为差分正弦波。它由 Art Metz 开发,Tektronix 拥有一项已过期的。
下面显示了一个改进和简化的四象限正弦波发生器。它由差分三角波电流驱动,输出为差分正弦波。它由 Art Metz 开发,Tektronix 拥有一项已过期的。 利用该电路可以实现远低于 0.1% 的 THD 值。
利用该电路可以实现远低于 0.1% 的 THD 值。