什么是真值表？
　　逻辑系统的真值表列出了输入二进制变量及其结果输出的所有可能组合。逻辑系统的输出来自逻辑表达式——布尔表达式——将系统的输出与输入关联起来。
　　具有 n 个二进制输入的逻辑电路真值表将具有 2 个输入组合或行。例如，对于一个输入，只有两个可能的值，即 0 和 1；对于两个输入，有四种输入组合：00、01、10 和 11；对于三个输入，有八种输入组合：000、001、010、011、100、101、110 和 111。
　　在本文的所有进一步讨论中，我们将使用字母 A、B、...、N 来表示逻辑系统的 n 个输入，使用字母 Y 来表示输出。

　　表 1显示了图 1中双输入逻辑系统的真值表。对于这个特定的系统，当 A = B = 0 时，输出 Y = 0，对于所有其他输入组合，输出 Y = 1。

　　图 1.双输入逻辑系统。

　　　

     

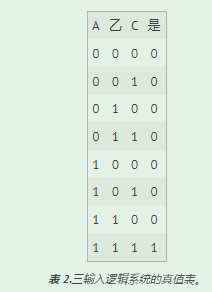
      表 1.双输入逻辑系统的真值表。

　　表2显示了图2中三输入逻辑系统的真值表。在本例中，我们假设当A = B = C = 1时，输出Y = 1，对于所有其他输入组合，输出Y = 0。

　　图 2.三输入逻辑系统。

　　

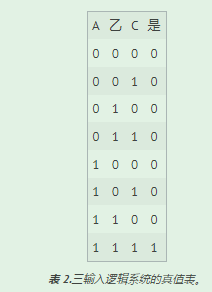
　表 2.三输入逻辑系统的真值表。

　　什么是逻辑门？
　　逻辑门是数字系统的初始构建块。每个主要逻辑门都是用于执行基本逻辑表达式的硬件或电子电路。
　　布尔代数定律有助于操纵二进制变量并简化逻辑表达式，但这些定律在数字系统中是通过称为逻辑门的电子电路来执行的。三种基本逻辑门是或、与和非。
　　在以下关于逻辑门的讨论中，我们忽略电压如何表示 1 和 0 以及晶体管如何处理它们。这样我们就可以深入讨论基础知识，而无需描述物理硬件。
　　或门

　　或门具有以下定义（正逻辑）：“如果一个或多个输入达到 1 状态，则或门的输出获得 1 状态。” 或门可以具有两个或更多输入和一个输出。

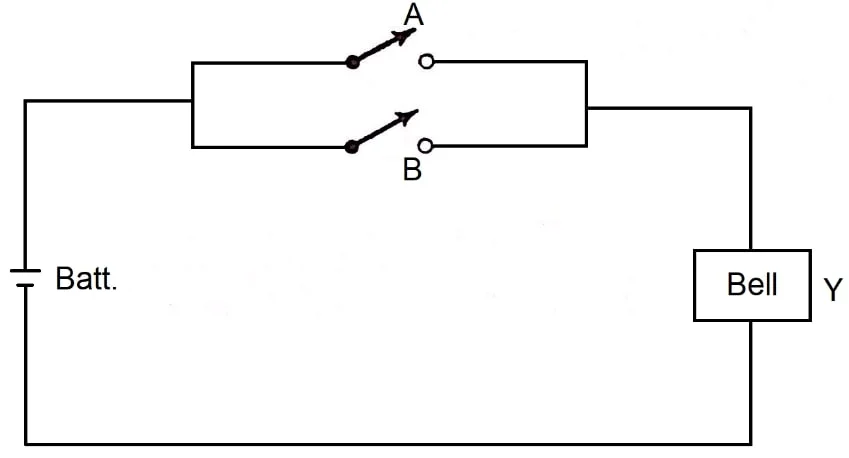
  　图 3的简单电路图显示了或门的基础。

　　图 3.或门的工作原理。
　　该电路通过两个开关 A 或 B 中的任意一个来激活铃铛 Y。我们可以观察到 A 或 B 或两者都会响铃。因此，这是一个或电路或开关逻辑术语中的或门，因为 A OR B = Y。
　　虽然我们在这个例子中使用了三个符号，但我们必须记住，只有两种状态：开和关。假设开 = 1 且关 = 0（正逻辑），我们可以说 1 OR 1 = 1，这意味着如果其中一个或两个开关处于开（1）状态，则铃也将处于开（1）状态。
　　如前所述，在布尔代数中，“+”符号是逻辑连接，表示或函数。因此，A + B 表示表达式 A OR B，而不是算术和。

　　图 4显示了或门的标准符号以及该门的布尔表达式。该表达式表明 Y 等于 A 或 B 或... 或 N。

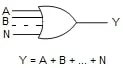
　　图 4.或门的标准符号及其布尔表达式。
　　请注意，上面的表 1与双输入或门的真值表相匹配。
　　或“+”门的一些布尔恒等式是：
　　A + B + C = (A + B) + C = A + (B + C)
　　A + B = B + A
　　A+A=A
　　A + 1 = 1
　　A + 0 = A
　　与门

　　与门具有以下定义（正逻辑）：“当且仅当所有输入都达到 1 状态时，与门的输出才获得 1 状态。” 与门可以具有两个或更多输入和一个输出。

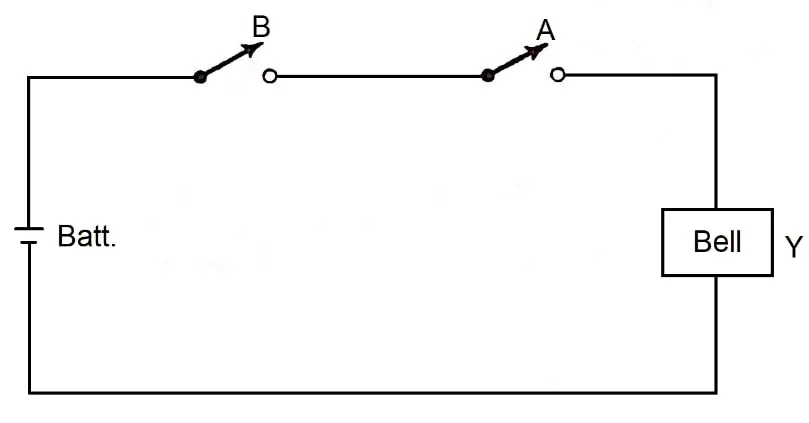
　　图 5的简单图表显示了与门的基础。
　　图 5.与门的工作原理。
　　在这种情况下，开关 A 和 B 必须同时闭合才能响铃。从逻辑上可以确定 A AND B = Y。在开关逻辑术语中，此配置为 AND 电路或 AND 门。
　　请注意，1 AND 1 = 1 - 如果两个开关都处于开启 (1) 状态，则铃也将处于开启 (1) 状态。
　　如前所述，在布尔代数中，“?”号是逻辑连接，表示 AND 函数。因此，A?B 表示表达式 A AND B，但不表示其乘法的算术意义。省略“?”号是可以的。

　　图 6显示了与门的标准符号以及该门的布尔表达式。该表达式表明 Y 等于 A 和 B 和... 和 N。

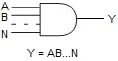
　　图 6.与门的标准符号及其布尔表达式。
　　请注意，上表 2与三输入与门的真值表相匹配。
　　AND“”门的一些布尔恒等式是：
　　ABC = (AB) C = A (BC)
　　AB = BA
　　AA = A
　　A1=A
　　A0=0
　　A（B + C）= AB + AC
　　A + AB = A
　　A + BC = (A + B) (A + C)
　　非门或反相电路
　　非门电路有一个输入和一个输出；其输出是输入的补码。
　　逻辑非具有以下定义：“非门的输出总是处于与输入相反的状态”。
　　如果我们将输入信号指定为 A，则输出信号不是 A。符号上方的线表示变量的补码或否定。因此，? 表示不是 A，如果 A 表示 1，则表达式  表示 0。如果 A = 0，则 ? = 1。同样，

　ˉˉˉ1=0和ˉˉˉ0=1。　

  　指定 NOT 函数的另一种常见方法是在输入变量后放置撇号，例如 A'。

　　该电路的另一个名称是反相器，因为它根据输入反转输出。
　　逻辑否定的标准符号是信号线与逻辑符号连接处的一个小圆圈。反转圆是示意图中显示反转的常用方法。

　　图 7显示了逻辑块输入处的逻辑非，图 8显示了逻辑块输出处的逻辑非。

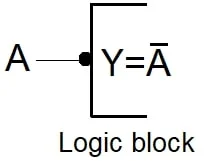
　　图 7.输入处的逻辑非。

　　图 8.输出处的逻辑非。

　　图 9显示了非门电路的熟悉符号以及该门的布尔表达式。

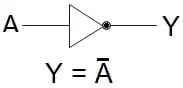
　　该表达式表明 Y 不等于 A，或者 Y 是 A 的补码。
　　表 3显示了非门或反相逻辑门的真值表。
　　A是
　　01
　　10
　　表 3.非逻辑门的真值表。
　　非门的一些布尔恒等式是：　

ˉˉˉˉˉˉˉˉA=A

ā+A=1

āA=0

A+AB=A+B

　　理解逻辑电路
　　布尔代数是逻辑设计人员简化复杂逻辑表达式的主要工具之一。该代数由一组符号和操作它们的规则组成。
　　真值表定义了逻辑电路的功能。它列出了逻辑电路的所有可能输入组合及其对应的输出。
　　逻辑门这个术语指的是执行二进制系统基本功能的数字电路。
　　当任一输入为 1 时，或门的输出将为 1。逻辑运算符符号是加号“+”。
　　只有所有输入都是 1，与门的输出才会为 1。逻辑运算符符号是点“?”。
　　非门的输出是输入的补码。非运算也称为反相。反相器的符号是信号线与逻辑符号连接处的一个小圆圈。