LTspice 反相器电路。

　　添加了负载电阻和电容的 CMOS 反相器的 LTspice 示意图。

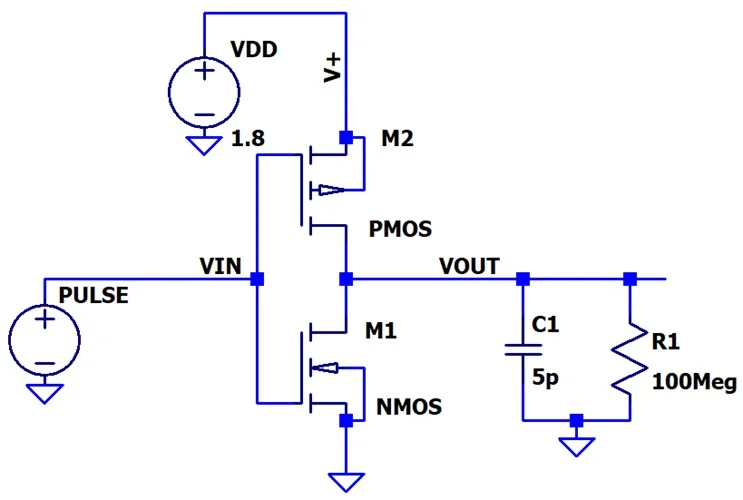
　　图 1.带负载电阻和电容的 CMOS 反相器的 LTspice 原理图。
　　在本文中，我们将继续使用上述示意图，研究“短路”或“击穿”电流。这两个术语指的是输出转换期间流过图 1 中 NMOS 和 PMOS 晶体管的电流。
　　短路电流流动是可能的，因为随着输入电压（控制两个晶体管的栅极电压）的变化，逆变器会经过 NMOS 通道和 PMOS 通道均导电的电气区域。
　　测量短路电流
　　我们只想测量由于击穿而从V DD流到地的电流。这意味着我们必须排除转换期间对负载电容器 C1 进行充电和放电的电流。
　　输出上升沿转换期间的短路电流
　　在图 2 中，我们放大了反相电路的中心部分。低到高输出转换的探针位置由 NMOS 晶体管 (M1) 漏极处的绿点表示。

　　绿点表示当输出从逻辑低变为逻辑高时我们测量击穿电流的位置。

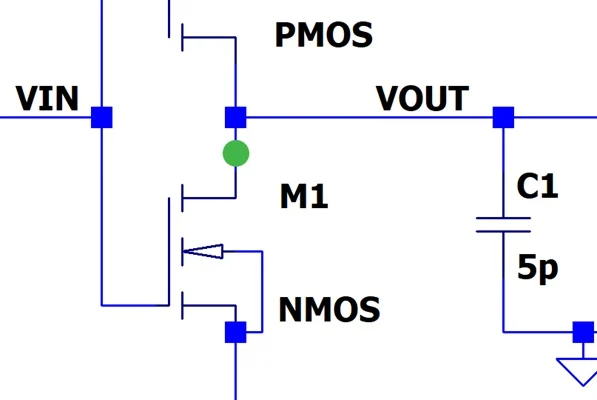
　　图 2.绿点表示当输出从逻辑低变为逻辑高时我们测量击穿电流的位置。
　　在低至高输出转换期间，充电电流流向：
　　来自V DD。
　　通过PMOS晶体管（M2）。
　　到负载电容器（C1）。
　　同时，短路电流流过：
　　来自V DD。
　　通过PMOS晶体管。
　　通过NMOS晶体管。
　　接地。
　　通过探测图 2 中绿点标记的导线段，我们测量了充电电流转向电容器后流过两个晶体管的电流。模拟结果如图 3 所示。

　　输出上升转换期间的逆变器直通电流。

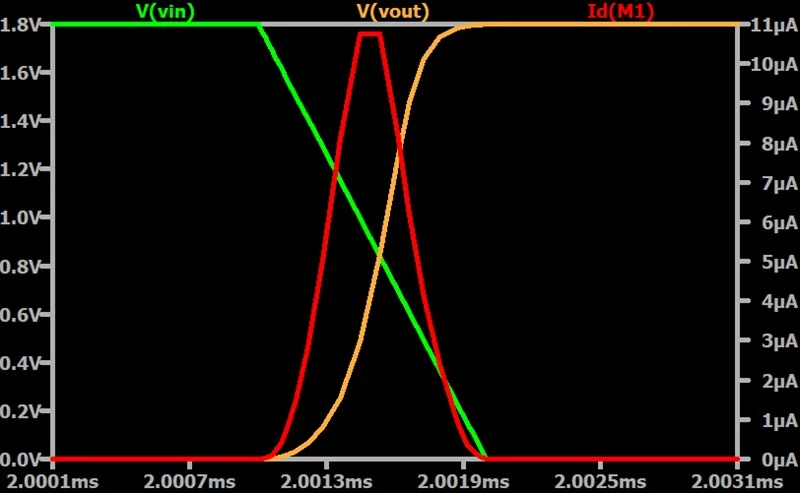
　　图3.输出上升转换期间的逆变器直通电流。
　　当输入为 0.9 V 时，测量电流达到峰值。在此电压下，NMOS 和 PMOS 晶体管均处于弱导通状态。这允许电流直接从V DD流到地。
　　输出下降沿转换期间的短路电流
　　对于高到低的输出转换，情况正好相反。放电电流流向：
　　来自负载电容器。
　　通过NMOS晶体管（M1）
　　接地。
　　然而，短路电流的路径保持不变。它仍然通过 M2，然后通过 M1 到达地。因此，我们在 PMOS 晶体管漏极处探测电流，该处位于放电电流从电容器到达的节点之前。探测位置在图 4 中标记。

　　绿点表示当输出从逻辑高变为逻辑低时我们测量击穿电流的位置。

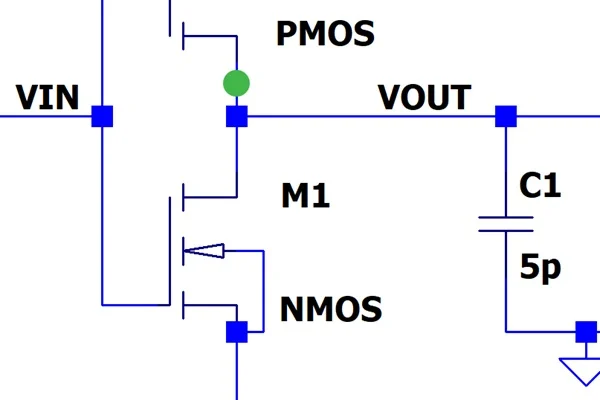
　　图 4.绿点表示当输出从逻辑高变为逻辑低时我们测量击穿电流的位置。

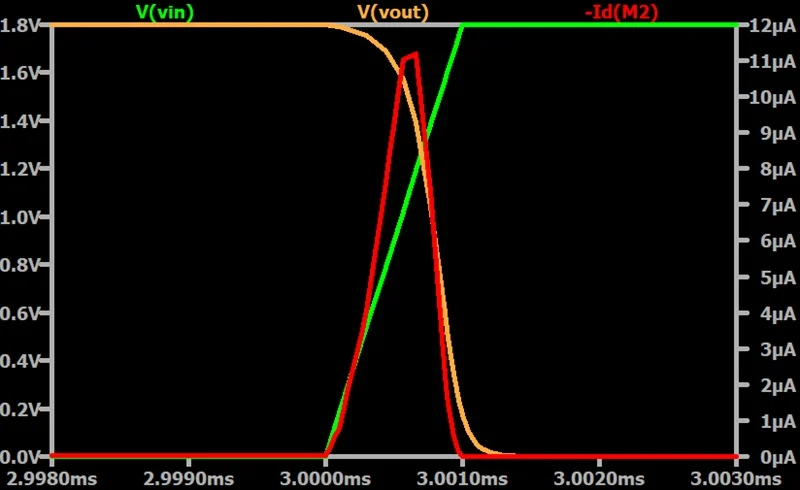
　　图 5 显示了下降输出转换的 LTspice 模拟结果。
　　输出下降转换期间的逆变器直通电流。
　　图5.输出下降沿期间的逆变器直通电流。
　　同样，当输入电压接近其中点 0.9 V 时，电流达到峰值。该短路电流在流过 NMOS 和 PMOS 电阻时会导致功率耗散。
　　测量瞬时功率耗散
　　有两个因素阻碍我们轻松地将晶体管电流测量值转换为功率耗散的数值估计值：
　　电流没有流过固定电阻，因此我们不能直接应用P = I 2 R。
　　晶体管的漏极 - 源极电压不是恒定的，所以我们不能直接应用P = IV。
　　然而，LTspice 并不反对执行必要的计算。如果您在单击组件时按下 Alt 键（在 Mac 上为 Cmd），LTspice 将绘制该组件的瞬时功率耗散。让我们尝试一下。

　　产出上升转型

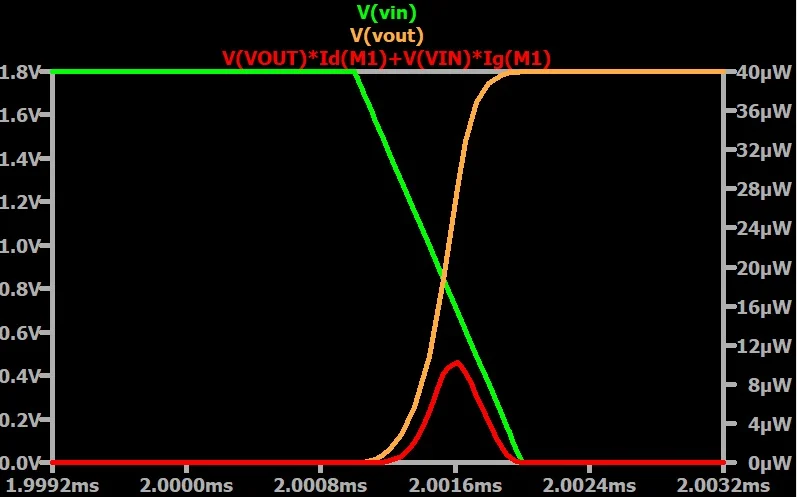
　　图 6 中的红色曲线描绘了 NMOS 在低至高输出转换期间消耗的功率。由于在上升转换期间没有充电或放电电流流过 NMOS，因此该功率耗散主要来自短路电流。
　　低至高输出转换期间的瞬时 NMOS 功率耗散。
　　图 6.低至高输出转换期间瞬时 NMOS 功率耗散。
　　相比之下，图 7 显示了 PMOS 在相同转换期间的瞬时功耗。由于充电电流确实流过该晶体管，因此其功耗明显较高。

　　低至高输出转换期间的瞬时 PMOS 功率耗散。

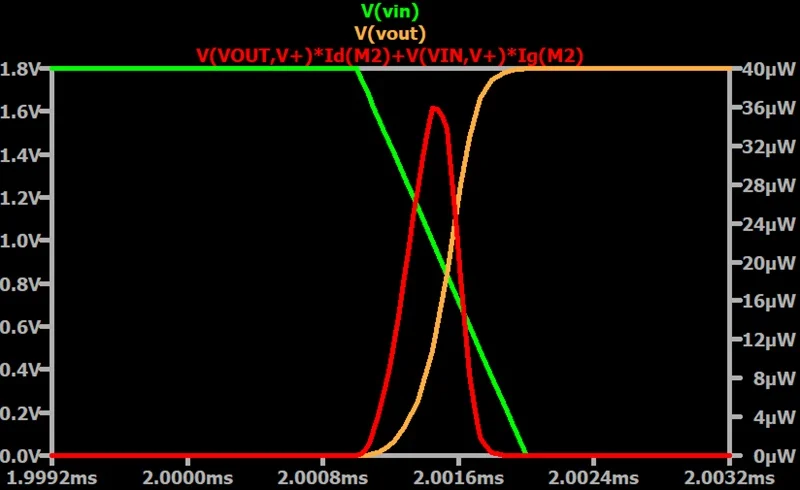
　　图 7.低至高输出转换期间的瞬时 PMOS 功率耗散。
　　衰落的转变
　　对于高至低输出转换，电容电流流过 NMOS 而不是 PMOS。NMOS 的功耗（图 8）现在大于 PMOS 的功耗（图 9）。

　　高至低输出转换期间 NMOS 的瞬时功率耗散。

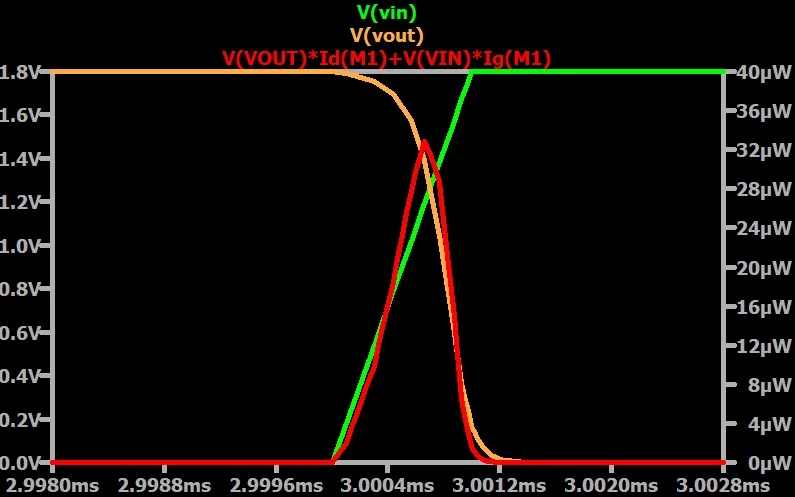
　　图 8.高至低输出转换期间 NMOS 的瞬时功率耗散。

　　高至低输出转换期间 PMOS 的瞬时功率耗散。

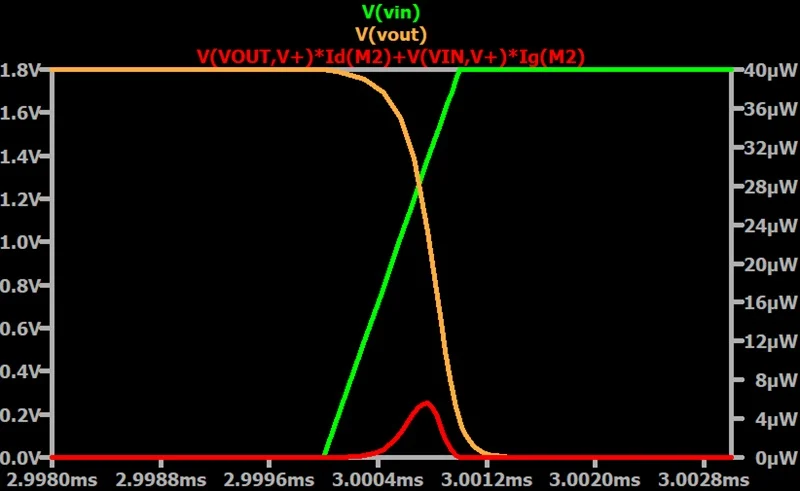
　　图 9.高至低输出转换期间 PMOS 的瞬时功率耗散。
　　对于下降沿转换，PMOS 是我们要检查的组件，以找到逆变器的短路功率耗散。
　　LTspice 如何获得这些结果？

　　LTspice 不仅能计算功率，还能通过迹线标签让我们知道它是如何执行计算的。例如，我们可以看到，在上升沿期间，NMOS（M1）的功率耗散等于：

    PM 1 =（ V O U T × I d （M 1 ））+（ V I N × I g （M 1 ））    

　　
　　其中I d是晶体管的漏极电流（短路电流），I g是栅极电流。
　　同一转换期间 PMOS（M2）的功率耗散为：
　PM 2 =（ V （V O U T ，V +） × I d （M 2 ））+（ V （V I N，V +） × I g （M 2 ））

　　其中V +指的是电源电压（我们原始原理图中的V DD ）。
　　在这个特定中，功耗几乎完全归因于漏极电流。然而，两个方程中都有I g，这提醒我们，栅极电流也会影响总功耗。
　　能量损失和平均功率耗散
　　终，本系列文章中的概念和模拟旨在提供用于分析 CMOS 反相器动态功耗的工具包。本着这种精神，我想在结束之前再介绍一下 LTspice 的功能。虽然它不会帮助我们了解有关短路功率的任何其他信息，但它与动态功耗这一更广泛的主题完全相关。

　　如果我们按住 Ctrl 并单击其中一个瞬时功率波形的迹线标签，LTspice 将打开一个光标框。此框底部的字段标记为“积分”，模拟转换过程中损失的能量。例如，图 10 显示了 NMOS 在低到高输出转换过程中的总能量损失。

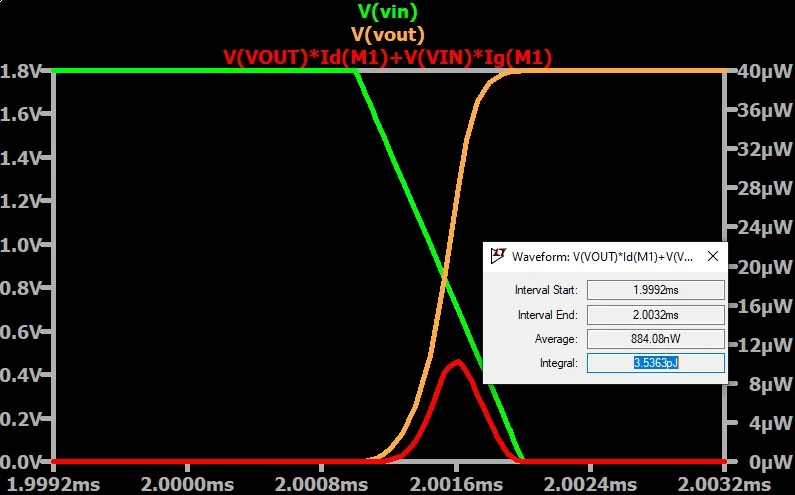
　　上升转换过程中通过 NMOS 晶体管损失的能量。
　　图 10.上升转换过程中通过 NMOS 晶体管的能量损失。
　　图 11 显示了下降沿转换的总 NMOS 能量损失。

　　下降沿转换过程中通过 NMOS 的能量损失。

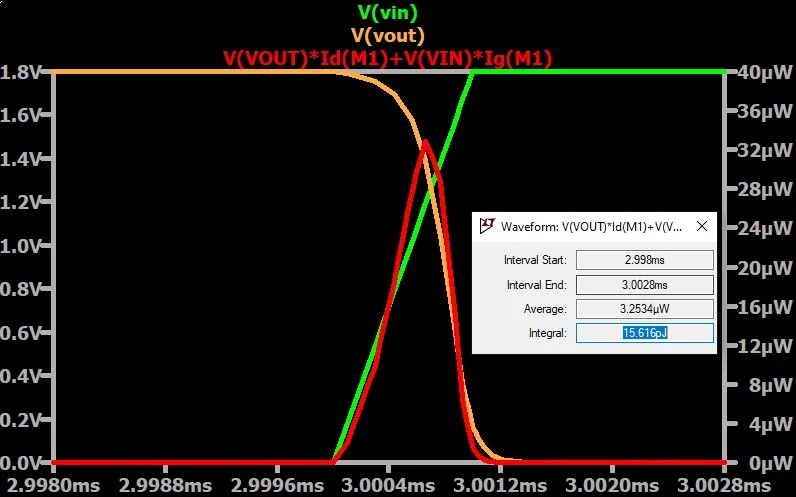
　　图 11.下降沿转换期间通过 NMOS 的能量损失。
　　一旦我们找到 PMOS 的总能量损耗（图 12 和 13），我们就可以估算出逆变器的平均动态功率耗散。

　　上升转换期间通过 PMOS 损失的能量。

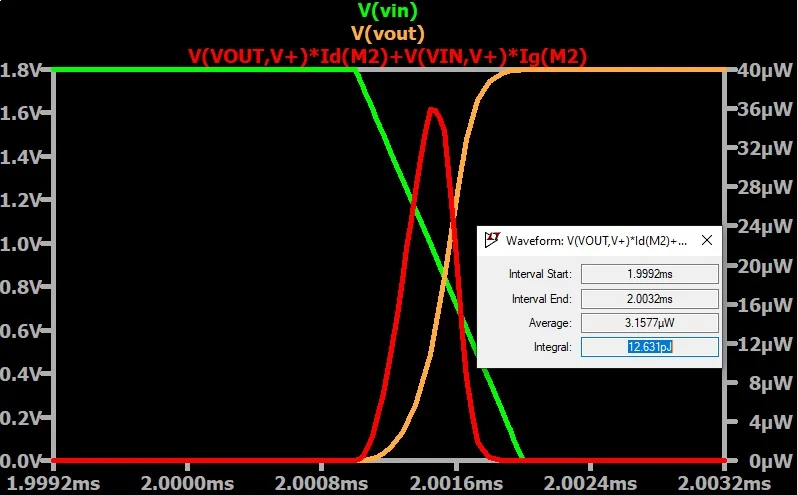
　　图 12.上升沿期间通过 PMOS 的能量损失。

　　下降沿转换期间通过 PMOS 损失的能量。

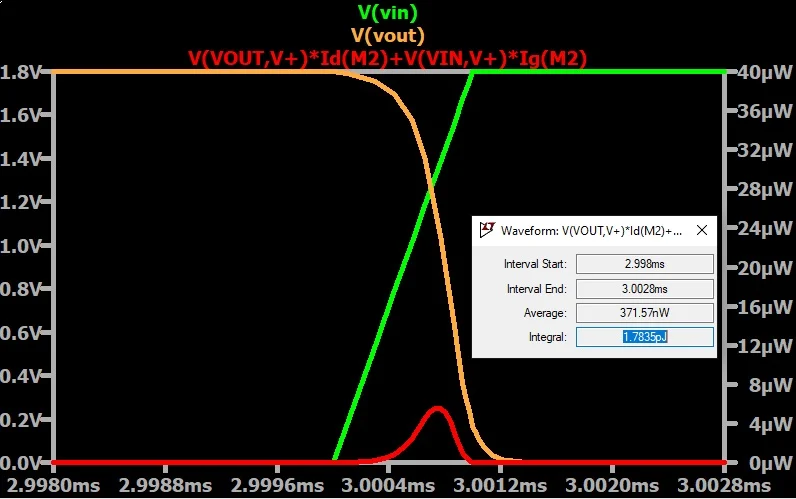
　　图 13.下降沿转换过程中通过 PMOS 的能量损失。
　　为了方便参考，能量损失值在表 1 中重现。请注意右侧的“总计”列 - 我们稍后会使用这些数字。
　　表 1.上升和下降转换期间晶体管的总能量损失。
　

　我们现在可以估算逆变器的平均动态功率耗散如下：　P平均值=( P上升+ P下降) × f   

　其中f是每秒的周期数。

　　对于此模拟，我们有P上升= 16.2 pJ 和P下降= 17.4 pJ。假设逆变器以 500 Hz 切换。回想一下，一瓦等于每秒一焦耳 (1 W = 1 J/s)，这给了我们估计的功耗：
　P平均值=(16.2pJ+17.4pJ)×500Hz=16.8nW       
　　至此，您已准备好尝试减少 CMOS 反相器中的动态电流和功耗的技术。至此，我关于 CMOS 反相器功耗的系列文章就结束了，不过我们以后可能会再讨论这些模拟。与此同时，我希望您觉得我们的讨论有所帮助。