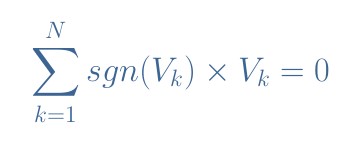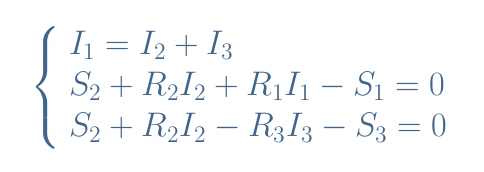在本教程中，我们介绍了基本、重要的电路定律之一。这些法律由德国医生古斯塔夫·基尔霍夫 (Gustav Kirchoff) 于 1845 年命名并制定。与许多物理定律一样，基尔霍夫电路定律(KCL) 相对容易理解，并且是从能量守恒定律的观察中得出的，这可能是物理学中古老和基本的原理之一。尽管如此，KCL 可能简单且易于理解，它们仍然是电路分析中需要掌握的基本工具，并且至今仍被广泛使用。KCL 由与定义电路能量的物理值相关的两个不同定律组成：电流和电压。下面我们分别分两节介绍基尔霍夫电流定律和电压定律。在这些部分之前，值得在部分中介绍使用 KCL 定律的框架以及与该原则相关的许多定义。第三部分展示了如何将 KCL 应用到实际电路并解决未知参数问题的示例。，一节简要介绍了 KCL 对于某些特定情况的限制。
　　框架和定义

　　应用基尔霍夫定律的框架是电路，它由两个极与闭环配置中的组件中间连接的电源或发电机组成。电路根据集总元件模型绘制，该模型假设元件为理想元件，相关表示如下图 1所示：

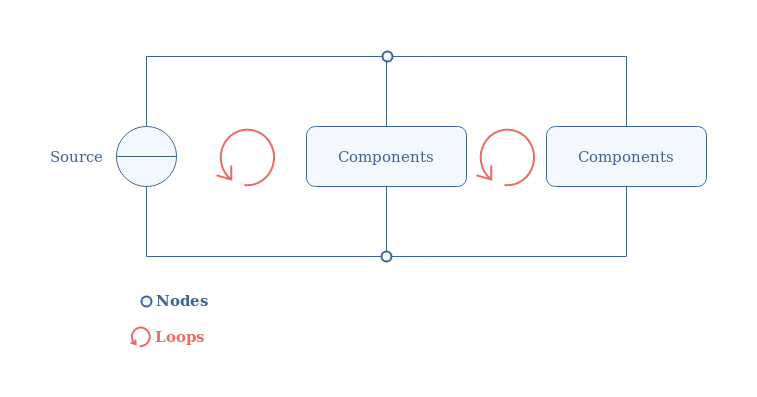
　　图 1：电路的集总元件模型
　　我们可以提供一些有关电路拓扑的具体细节。直线是电路不同元件之间的理想连接/电线，这意味着它们不呈现电阻或电抗行为，因此不存在功率损耗或相移现象。电源为电路提供电源，电源由电压和电流信号（直流或交流）组成。这些元件是无源的，它们由电阻器、电容器和电感器的组合组成。它们可以并联连接（如图1所示），也可以串联连接。本教程不考虑放大器等有源组件，因为它们与外部电源相关。用电线连接两端的一组元件称为分支。为了稍后充分理解基尔霍夫定律，两个重要的拓扑定义非常重要：节点和环。节点代表分支之间的连接点，它们在图 1中用蓝色圆圈突出显示。上图中的红色圆圈箭头突出显示了循环，它表示分支的闭合路径。
　　基尔霍夫电流定律

　　电流定律也称为节点定律或结点定律，规定在节点处相遇的电流的代数和等于零。可以用连接三个分支的节点来说明一个简单的示例：

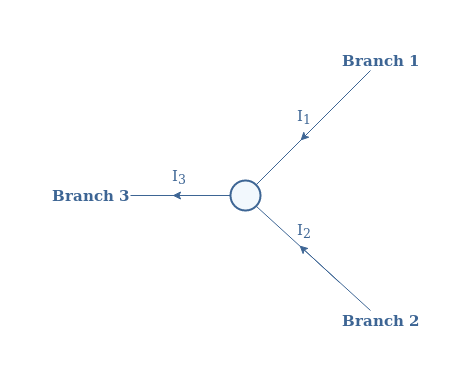
　　图2：三个分支的节点连接
　　因此，该定律规定进入节点的电流总和等于离开结点的电流。在我们的示例中，这句话在数学上翻译为I 1 +I 2 =I 3 或I 1 +I 2 -I 3 =0，当前 I 3为负，因为它正在退出节点。在一般情况下，N个分支的节点结点的电流被标记为I 1，I 2，…，I N满足以下方程1：
　　eq 1：基尔霍夫电流定律
　　如果电流 I k 进入节点，则符号函数sgn等于+1 ；如果存在，则符号函数 sgn等于-1 。节点定律是根据封闭系统中电荷不变的观察直接写出的。这种假设也称为电荷守恒定律。 在物理学中，原理是指没有经验证明无效但尚未被证明的观察结果，相当于数学中的假设。
　　基尔霍夫电压定律

　　电压定律也称为环路规则，它与节点规则非常相似，但适用于环路而不是节点。第二定律指出电路环路中电压的代数和为零。可以用为串联 RC 滤波器供电的直流电源来说明一个简单的示例：

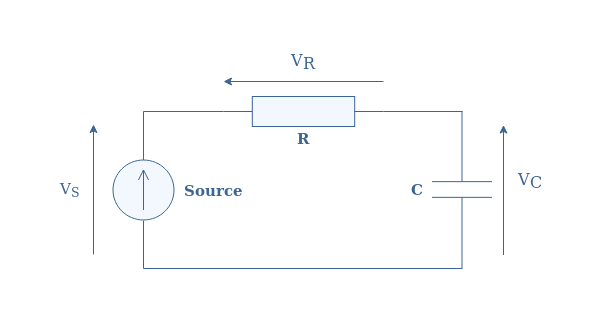
　　图 3：具有三种不同电压的环路

　　电压的符号由箭头的方向决定，通常认为源为正，因此顺时针箭头为正，逆时针箭头为负。因此，基尔霍夫电压定律指出V S =V R +V C或V S -V R -V C =0。对于具有 N 次电压 V 1、V 2、…、V N生成和下降的环路，满足等式2 ：

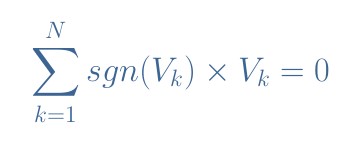
　　eq 2：基尔霍夫电压定律
　　当产生电压时（我们示例中的源），符号函数 sgn 等于+1 ；当观察到电压降时，符号函数 sgn 等于-1 （使用图 3中的无源组件）。
　　伦敦大学学院申请

　　在本节中，我们将展示使用 KCL 可以解决的典型问题的解决过程。考虑图 4所示配置中与电阻器 R 1、R 2和 R 3连接的三个源 S 1、S 2和 S 3：

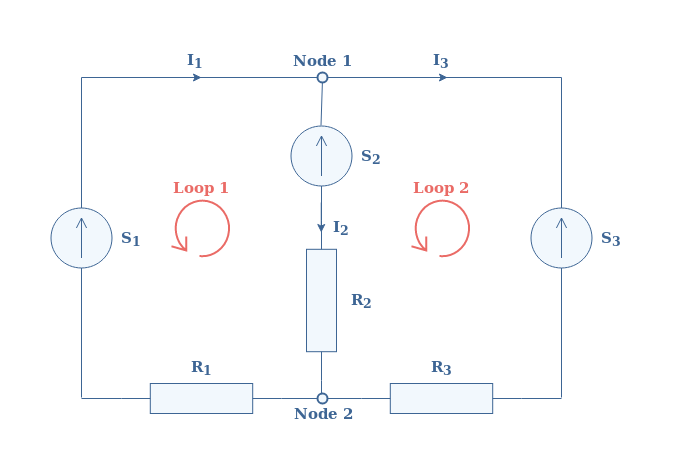
　　图 4：电路配置示例

　　电源是直流且理想的，这意味着它们不存在内阻。我们取S 1 = 4 V，S 2 = 3 V，S 3 = 10 V，并且R 1 = 3 Ω，R 2 = 2 Ω，R 3 = 1 Ω。根据基尔霍夫现行定律，我们可以为节点 1 和 2 写出以下等式：节点1： I 1 =I 2 +I 3节点2： I 2 +I 3 =I 1与节点1的方程类似根据基尔霍夫电压定律，我们写出循环 1 和循环 2 的等式：循环1： S 1 =S 2 +R 2 ×I 2 +R 1 ×I 1循环2： S 2 +R 2 ×I 2 =S 3 +R 3 ×I 3我们可以以不同的方式编写这些方程，以获得以下具有 3 个未知参数 I 1、I 2和 I 3 的3 个方程组：

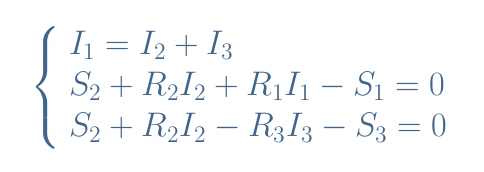
　　eq 3：KCL 线性方程组
　　该方程组可以用消除法求解，即在第二行（L2）中将 I 1替换为 I 2 +I 3 ，并通过加法 R 3 ×L2+R 1 ×L3消除项 I 3 。我们直接找到I 2 =4.2 A，然后我们可以通过替换 L3 中的 I 2来找到 I 3，得到I 3 =1.4 A，我们得到I 1 =I 2 +I 3 =5.6 A。
　　KCL 的局限性
　　在部分中，我们已经了解了 KCL 应用的框架，但电路还必须遵守一些其他更微妙的条件。我们在本节中简要强调了 KCL 有效的进一步条件。个条件称为准静态近似，即信号的传播时间与信号的周期相比必须可以忽略不计，这给出了电路尺寸的条件。例如，考虑200 kHz (T=5 μs) 的交流信号，如果接收器位于电路中D=10 cm处，则传播时间将为 Δt=D/c=0.33 ns，其中 c 为速度光。在这种情况下，Δt<<T，准静态近似有效并且遵守应用 KCL 的条件。然而，如果接收器位于D=1 km处，则传播时间变为 Δt=3.3 μs，并且不遵守不等式 Δt<<T，因此近似无效，并且 KCL 无法应用于电路。 在准静态近似中，源的任何变化都被认为会立即传播到电路中的任何点，从而避免了可能使 KCL 失效的延迟效应。这个肯定可以用麦克斯韦-安培方程来证明，其中当准静态近似有效时可以消除变分项，然后可以用格林-奥斯特罗格拉茨基定理来证明基尔霍夫电流定律。赋予 KCL 有效性的另一个常见条件是电路回路上的磁通量的变化必须可以忽略不计。根据感应定律，磁通量的变化会在电路中产生感应电流，从而产生感应电压。 磁通的变化引入了一个新的电压项，该电压项不是由元件或电路的拓扑结构解释的，而是来自外部源，从而使环路规则失效。
　　结论
　　KCL 是电子学的基本定律，可应用于由环路和节点构成的电路。这些拓扑定义以及其他拓扑定义在本文的部分中介绍，该部分提供了应用 KCL 的框架。基尔霍夫定律由电流定律和电压定律组成，反映了电路中能量守恒定律。电流定律解释了电荷守恒，它指出节点中电流的代数和等于零。电压定律规定环路中电压的代数和为零。进一步的章节介绍了使用这两个定律可以通过求解线性方程组来解决典型的电子问题。，我们在一节中简要介绍了为了使 KCL 有效，必须考虑有关电路尺寸和外部磁通量存在的一些微妙条件。