网格分析是计算电子电路内电流的非常方便的工具。通过了解每个网格（部分）内的电流，我们可以求解每个组件的电压和功率（瓦）。工程师和设计师利用这些信息来选择正确的部件，在通电时不会发出神奇的白烟。
　　　
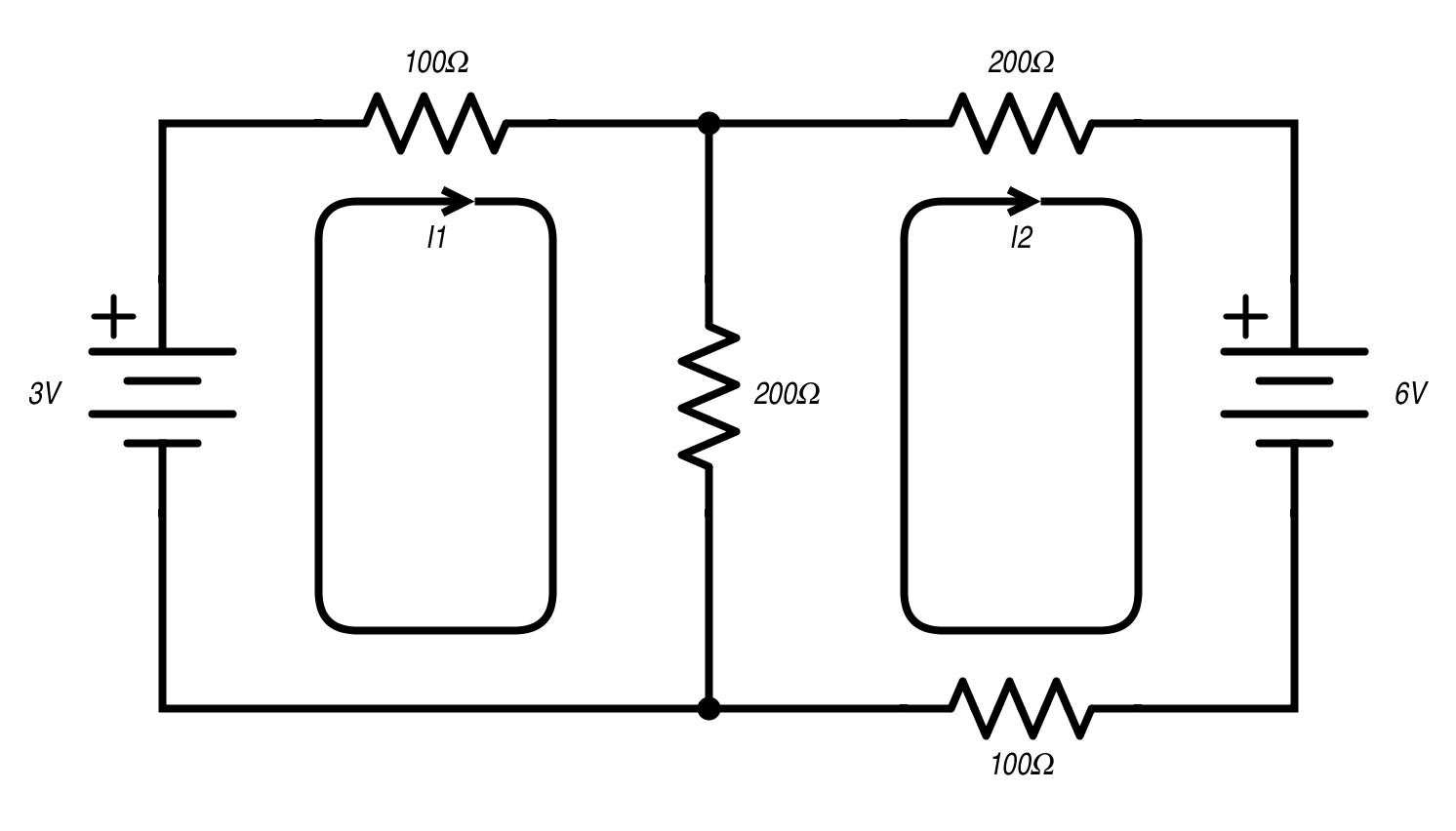
　　我们可以将上面的示例分为两个网格， I 1和 I 2。I 1表示网格1中的虚拟电流。I 2表示网格2中的虚拟电流。网格电流通常以顺时针方向描绘。从这里开始，我们将每个网格写成线性方程，并使用求解工具找到 I 1和 I 2。
　　使用基尔霍夫电压定律 (KVL)，网格 I 1可写为：?3 v+100Ω(I1)+200Ω(I1?I2)=0
　　I 1 -I 2是因为流经中心200Ω电阻的电流是两个网格之间的差异。由于I 1顺时针流动，电池的(-)侧被记录为电压。

　　电池将被视为独立的电压源。如果我们用压控电压源 (VCVS)（例如真空管或 FET 电路）替换其中之一，会发生什么？

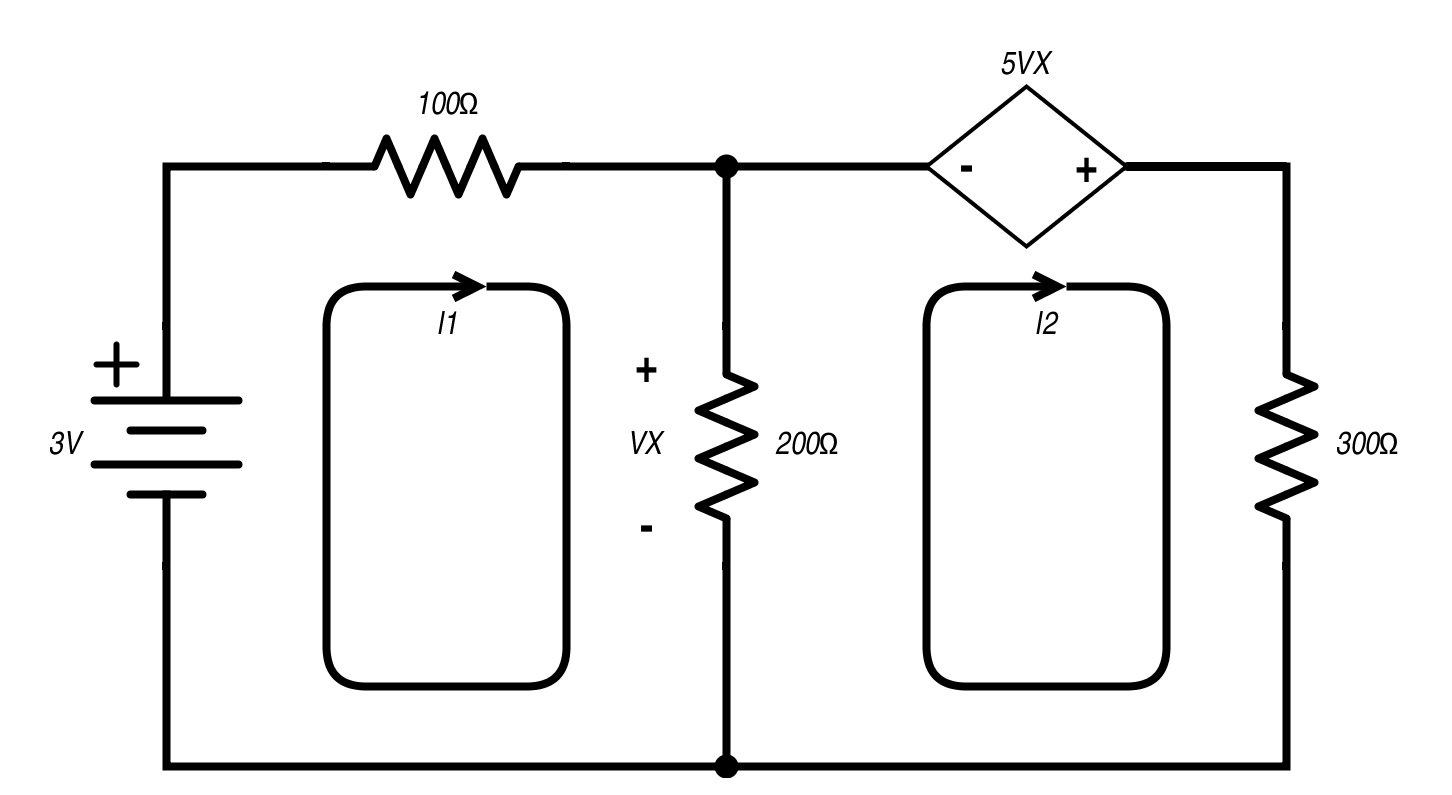
　　网格分析　　
　　I 1网格的公式与前面的示例相同。　　
　　此时，相关电压源是一个比率，而不是一个固定数字。为了能够求解这个系统，我们需要编写 VX 的公式。将电阻 200 Ω 乘以电流即可得出。
　　由于两个网格都使用该电阻器，因此电流为：
　　对于求解器，V X将被注释为“c”。
　　将三个线性方程（方程 3、4 和 5）放入 Wolfram Alpha 友好语法中：
　　等式的结果为：I 1的电流为 21.429 mA，I 2的电流为 17.143 mA，V X 的电压为 0.857 V。我们的依赖源增益为 5，因此产生 4.286 伏电压。这时，有人在想：“嘿，等一下。如果依赖电源的电压低于它所更换的电池，为什么在第二个示例中 I 1的电流更大？” 不错的收获！我们交换了相关源的极性，I 1和 I 2电流都跳变了。希望这是有计划的，我们的电路不会像烤面包机里的袜子一样冒烟。
　　其他相关源包括电流控制电压源 (CCVS)、电压控制电流源 (VCCS) 和电流控制电流源 (CCCS)。双极结型晶体管是 CCCS 的一个很好的例子。
　　在规划使用放大器或放大组件的电路时，理解具有相关源的网格分析非常重要。这些方法与没有依赖源的方法几乎相同，只是需要提供更多信息来实现解决方案。