本文介绍了有关带隙电路的一些基本信息，这些电路广泛用于生成与温度无关的参考电压。
　　带隙参考技术是创建与温度无关的参考电压常用的方法之一。
　　传奇电子工程师 Bob Widlar 在 20 世纪 60 年代末为当今的带隙电压基准奠定了基础。在此之前，的半导体解决方案依赖于使用噪声大、温度敏感的齐纳二极管。除了这些缺点之外，基于齐纳二极管的方法还需要大于 5V 的电源电平。
　　我们将看到，正常的带隙电压基准可以产生低至约 1.23 V 的基准电压。此外，还有一组带隙基准，称为分数带隙，可以产生低至几毫伏的输出电压。　
　　什么是带隙参考？
　　电压基准的目标是生成稳定的电压，理想情况下该电压独立于温度和其他外部因素的变化。不幸的是，环境温度会影响电路内不同组件的特性。
　　例如，BJT 晶体管的基极-发射极电压是温度的线性函数，并且表现出约 -2 mV/°C 的温度系数。这种器件限制将影响电路输出。
　　如果我们无法获得更好的设备，我们将不得不以某种方式补偿温度引起的变化。例如，如果我们可以生成一个与温度成线性函数且具有 2 mV/°C 正温度系数的电压，那么我们也许能够补偿基极-发射极结引入的变化。
　　生成 2 mV/°C 温度系数的一种方法是注意以下方程给出的热电压 (VT) 是温度的线性函数：
　　
　　V_{T}=\frac{kT}{q}
　　
　　在此方程中，k是玻尔兹曼常数，q是单个电子携带的电荷，T 是开尔文温度。热电压的温度系数为$$\frac{k}{q}$$，约为+0.085 mV/°C。如您所见，温度系数为正，但远小于所需值 2 mV/°C。
　　为了解决这个问题，我们可以通过与温度无关的常数 M 来放大热电压，使得 $$\frac{Mk}{q}$$ 等于大约 2 mV/°C。这个概念是带隙基准的主要思想，如下图 1 所示。
　　
　　图 1图片由模拟集成电路分析与设计提供。    
　　
　　热电压由“V T发生器”块产生。该块的输出乘以适当的因子 M，然后添加到 BJT 的基极-发射极电压。理想情况下，总输出应与温度无关。
　　基本带隙具有弓形漂移曲线
　　我们假设基极-发射极电压的温度系数约为-2 mV/°C；然而，它并不是 100% 恒定的。这就是带隙输出不会完全独立于温度的原因。
　　只有在一个目标温度下，我们才能调整因子M，将参考输出的温度系数设置为零。当温度远离该目标时，基极-发射极电压的温度系数将略有变化。因此，带隙输出将随温度出现轻微变化。
　　基本带隙基准的典型输出曲线如图 2 所示。每条曲线对应于在某一特定温度下将温度系数设置为零。正如您所看到的，基本带隙基准的输出电压在绘制温度曲线时具有弓形漂移曲线。 
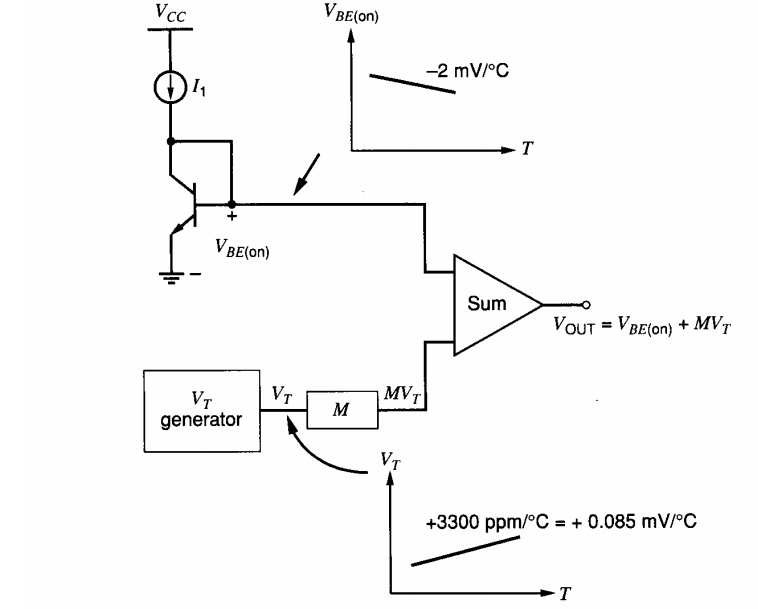
　　　　图 2图片由模拟集成电路分析与设计提供。   　
　　一些带隙基准采用温度补偿电路来进一步提高基本结构的漂移性能。例如，LT1019（精密带隙基准）的输出如图 3 所示。该器件采用了大大改进的曲率校正技术。
　　
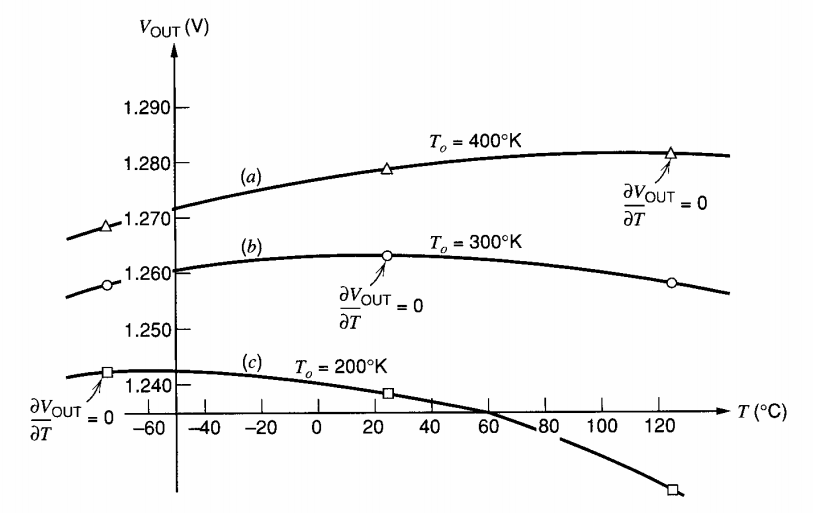
　　图 3图片由Linear Technology提供。
　　为什么他们称其为带隙参考？
　　对于上述讨论，我们假设基极-发射极电压的温度系数为 -2 mV/°C，并容易得出$$\frac{Mk}{q}$$ 应为 2 mV/°C。为了更准确，我们应该用器件参数来表达基极-发射极电压，并使用得到的方程来计算因子M。更多信息，您可以参考Analog Integrated Analysis and Design一书的4.4.3节电路。在这里，我们只看一个终的分析结果，其输出电压为：　　
　　$$V_{OUT}|_{T=T_{0}}=V_{G0}+\伽玛V_{T0}$$　　
　　V G0是硅的带隙电压，为1.205V。γ是与基极掺杂水平相关的参数。T 0表示带隙基准的温度系数设置为零时的温度。因此，热电压V T0和带隙输出 $$V_{OUT}|_{T=T_{0}}$$ 被视为 $$T=T_{0}$$。 
　　假设带隙输出在 $$T_{0}=300 K$$ 处设置为零。因此，我们有 $$V_{T0}=26 mV$$。假设γ的典型值= 3.2，我们得到　
　　V_{OUT}|_{T=300 K}=1.205 V + (3.2\times 26 mV)=1.2882 V
　　正如您所看到的，普通带隙基准的输出电压接近硅的带隙电压，这解释了此类电压基准的名称。现在我们已经熟悉了创建与温度无关的参考电压的基本思想，让我们看一下这个概念的电路实现。
　　Widlar 带隙参考
　　如图 1 所示，带隙基准电压源需要生成等于热电压的电压。我们可以生成与热电压成正比的电压，而不是生成等于V T的电压。然而，比例因子应该与温度无关，以便我们可以成功应用上一节中讨论的概念。让我们看看是否有一种简单的方法可以实现这一目标。我们知道 BJT 的基极-发射极电压由以下等式给出：　　
　V_{BE}=V_{T}ln\left (\frac{I_{c}}{I_{s}}\right )　　
　　其中I c和I s分别是集电极电流和饱和电流。如果I c和I s与温度无关，则基极-发射极电压将等于V T乘以与温度无关的因子 $$ln\left ( \frac{I_{c}}{I_{s}}\right ) $$。然而，我们知道比例因子与温度无关。让我们考虑一下两个晶体管Q 1和Q 2的V BE差异：　　
　V_{BE1}-V_{BE2}=V_{T}ln\left ( \frac{I_{c1}}{I_{s1}}\right )-V_{T}ln\left ( \frac{I_ {c2}}{I_{s2}}\right )=V_{T}ln\left ( \frac{I_{c1}}{I_{c2}} \frac{I_{s2}}{I_{s1}} \右）
　　
　　在这种情况下，我们可以通过设置集电极电流比 ($$\frac{I_{c1}}{I_{c2}}$$) 和饱和电流比，使V BE差成为热电压的常数因子($$\frac{I_{s2}}{I_{s1}}$$) 常数。缩放晶体管的发射极面积使我们能够设置饱和电流比。对于集电极电流比，我们可以简单地使用电流源来设置晶体管的偏置电流。因此，可以使VBE差成为热电压的恒定因子。带隙基准通常使用两个 BJT 的V BE差异来创建图 1 中的“V T发生器”块。 
　　作为示例，让我们看一下下面图 4 所示的简化 Widlar 带隙参考。
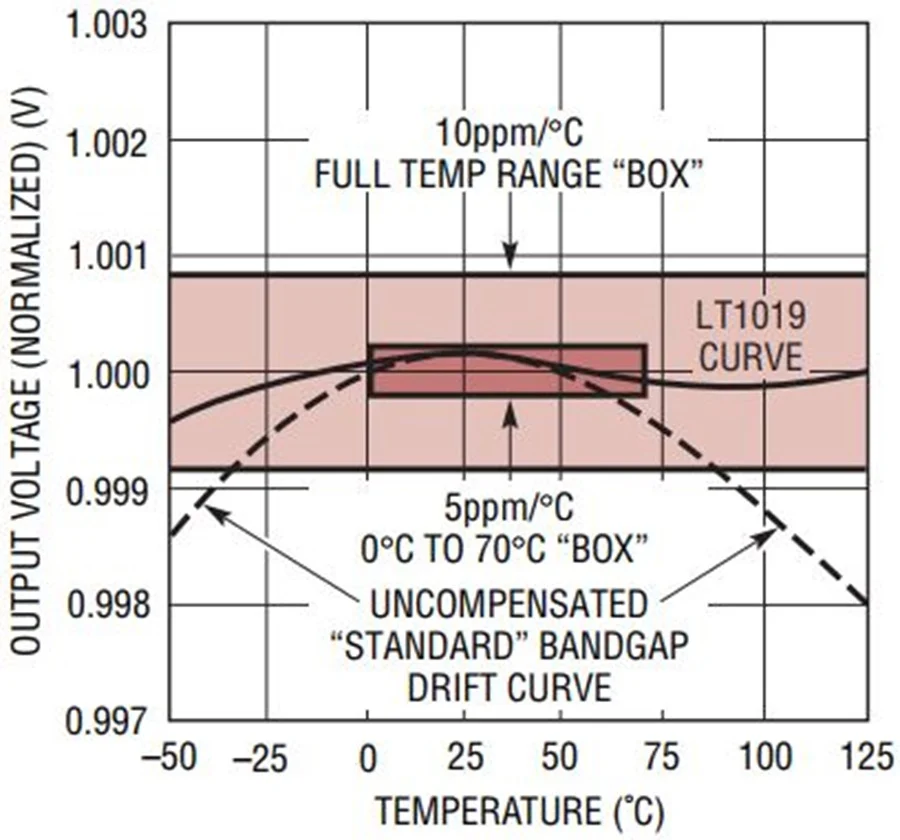
　　　　图 4图片由IEEE Explore提供。　
　　Q 1和Q 2的V BE以及R 3电阻器创建了一个环路。因此， R 3两端的电压降等于Q 1和Q 2之间的V BE差。这两个晶体管相同 ($$I_{s1}=I_{s2}$$)，但具有不同的集电极电流。假设$$V_{BE1}=V_{BE3}$$，电阻R 1和R 2具有相等的电压降。因此，集电极电流比 $$\frac{I_{c1}}{I_{c2}}$$ 等于电阻比 $$\frac{R_{2}}{R_{1}}$$ （我们忽略晶体管的基极电流）。因此， R 3上的电压降由下式给出 　　
　　$$\Delta V_{R3}=V_{BE1}-V_{BE2}=V_{T}ln\left ( \frac{I_{c1}}{I_{c2}} \frac{I_{s2}}{ I_{s1}}\right )=V_{T}ln\left ( \frac{R_{2}}{R_{1}}\right )$$　　
　代入图 4 中给出的电阻值，我们得到 　　
　　$$\Delta V_{R3}=V_{T}ln(10)=2.3V_{T}$$　
　　流经R 3 的电流等于R 2的电流，因此我们得到R 2上的压降为： 　
　　$$\Delta V_{R2}=\frac{\Delta V_{R3}}{R_{3}}\times R_{2}=\frac{R_{2}}{R_{3}}\times 2.3V_ {T}=23V_{T}$$　
　　参考输出等于 R2 压降加上Q 3的基极-发射极电压：　　
　　$$V_{REF}=V_{BE3}+23V_{T}$$　
　　假设 $$V_{BE3}=0.65 V$$ 和 $$V_{T}=26 mV$$，我们有 $$V_{REF}=1.248 V$$。此外，我们可以将温度系数值代入V BE3和V T并计算输出的温度系数： 　
　　$$\frac{\delta V_{REF}}{\delta T}\约-2mV/^{\circ}C+23\times 0.085mV/^{\circ}C=-0.045mV/^{\circ }C$$　
　　这远小于基极-发射极电压的温度系数。典型的带隙基准可以实现低至 20 ppm/°C 的温度系数。
　　带隙参考的后期发展
　　Widlar 的电压基准于 1971 年发布，为当今的带隙基准奠定了基础。尽管这是一项伟大的成就，但它仍然存在当前的驱动灵敏度限制。此外，它无法产生有用的电压电平，例如 2.5 V 和 5 V。这些问题后来通过 AP Brokaw 推出的突破性设计得到解决。这是个基于带隙的精密电压基准。
　　后来，研究人员开发了称为分数带隙的带隙基准，可以输出低至几毫伏的电压。有关这组带隙基准的更多信息，请参阅 JSSC 论文“具有低于 1V 操作的 CMOS 带隙基准电路”。