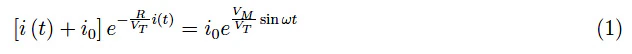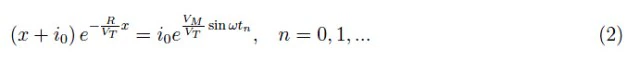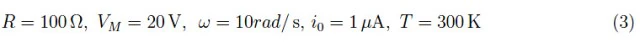限幅器电路 - 也称为鉴幅器（限幅器） - 类似于简单的半波整流器，不同之处在于输出信号是二极管两端的电压降，而不是电阻器两端的电压降。第二个新颖之处是与二极管串联的电池。
　　在分析这样的电路之前，有必要反思一下开发仿真软件时遇到的困难。在本期中，我们将展示传统的编程语言需要使用多行代码来实现例程，而使用Mathematica软件只需一行代码即可解决问题。
　　数值程序
　　让我们从简单的电路开始：由输入信号Vin ( t ) = V M sin ωt供电的电阻器R。我们将此量视为输出信号，而电流按因子R 1缩放。在这种情况下，模拟被认为是相同的，因为它再现了输入信号。
　　然后将二极管 D 与电阻器R串联插入，如图 1 所示。　　　

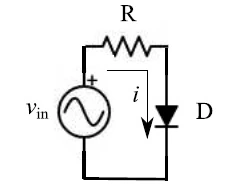
　图 1：电阻器与二极管串联。

　　图 1：串联电阻和二极管
　　通过应用基尔霍夫第二原理并考虑电压-电流特性，经过简单的步骤，我们得出以下方程：
　　电力电子科学笔记：限幅器电路简介
　　我们记得V T 是以伏特为单位的热当量，在室温下，它等于 26 mV。
　　因此，串联RD中流动的电流是式(1)的解。这被称为“函数方程”，因为未知数是函数而不是数字。
　　我们可以立即说方程（1）不能以封闭形式求解，因为我们无法获得电路中流动的电流i ( t )的解析表达式。之后，我们可以使用Mathematica进行数值计算，对连续变量t在周期区间 [0 , 2 π/ω ] 内进行离散采样，即方程（1）的第二个成员。结果是N 个解耦方程组：
　　电力电子科学笔记：限幅器电路简介
　　这可以通过Mathematica 的Solve 语句轻松解决。例如，对于：
　　电力电子科学笔记：限幅器电路简介　　解列表 { x 0 , x 1 , …, x N } 被绘制为t n的函数，如图 2所示 。通过连接连续线，我们获得如图 3 所示的趋势。

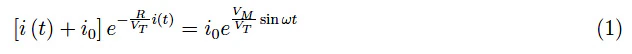
　　图 2：以数值方式得出的解 xn = in 的趋势。　　

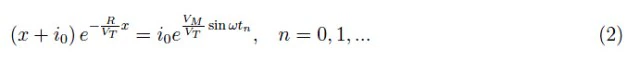
　　图 3：使用 ListLinePlot 指令获得的解 xn = in 的趋势。
　　图 3：使用 ListLinePlot 指令获得的解x n = i n的趋势
　　象征性程序
　　将函数方程（1）改写为以下形式更为方便：
　　电力电子科学笔记：限幅器电路简介
　　其中x ( t ) 是反向饱和电流归一化的电流强度，a = Ri 0 /V T，并且f ( t ) =  v in ( t )。在符号模式下工作，我们强制 Wolfram 语言内核通过 Solve 指令找到解x ( t ). 相应的输出通过Lambert W 函数表示，该函数在 Wolfram 语言中是内置的，并由指令ProductLog调用.　　对于正弦输入，假设电阻R和峰值V M 作为参数；对于角频率，我们照常假设ω = 20 rad/ s，请记住结果与该量无关。相反，R和VM是决定性的，尤其是二极管的 整流效果的峰值。例如，如果V M = 1mV，则无论R的值如何，二极管都不会进行整流，如图 4-5 的图表所示。

　　

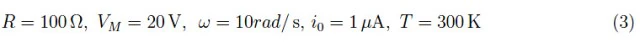
　图 4： R = 1Ω时以安培表示的电流趋势

　

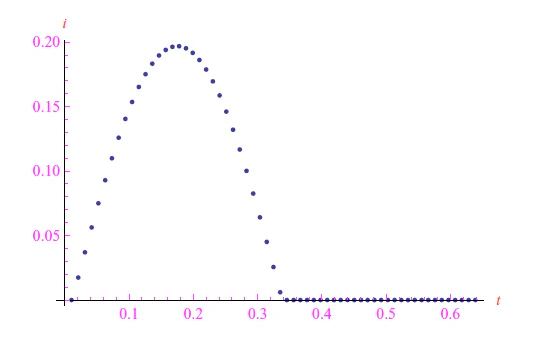
　　图 5： R = 1MΩ时以安培表示的电流趋势

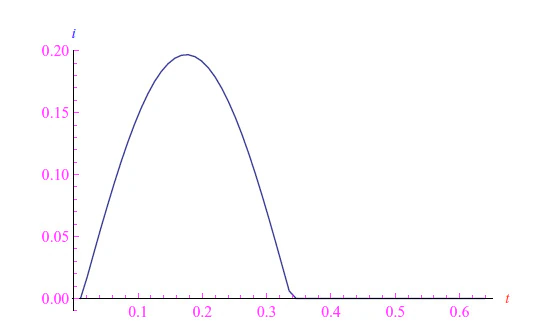
　　基本上，这种行为是由于输入信号归一化为热当量（以伏特为单位），即V T = 26 mV。输入的峰值相对于V T必须足够高。图 6 的图表证实了这一点，从图中我们可以看出，整流器实际上是理想的，但由于R值较低，无论如何它几乎都是正向偏置短路。当R = 1 MΩ 并保持输入峰值时，我们得到图 7 的图表。　　由于欧姆元件的线性，R上的电压降将具有与电流相同的趋势。否则，我们预计二极管两端的电压降会出现扭曲的趋势。如果我们使用Mathematica计算的数量，我们会发现图 8 的奇怪趋势，其中输入信号的负半波的峰值被截断。这是 Mathematica 内核在搜索方程 (4) 的解时发出警告的结果。为了验证上述内容，使用基尔霍夫第二原理计算电压v D 并绘制解决方案就足够了（见图 9）。

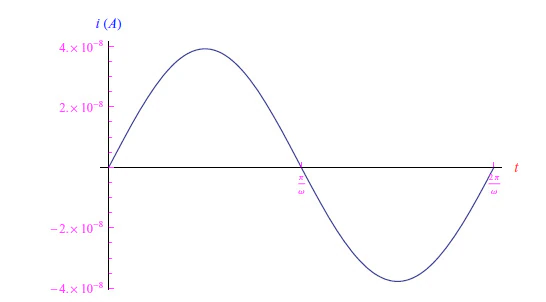
　　图 6：R = 1Ω 和 VM = 10V 时的电流强度趋势。　

　　图 7：R = 1MΩ 和 VM = 10V 时的电流强度趋势。

　

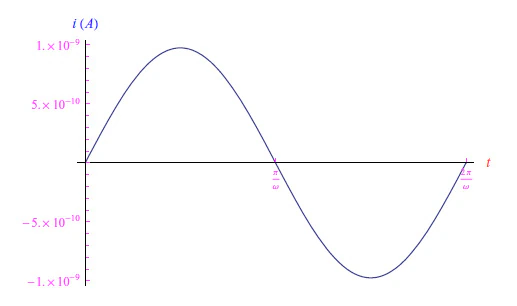
　　图 8： R = 10Ω 且VM = 1V时二极管两端压降的趋势

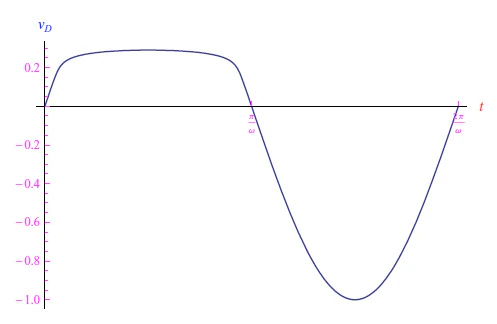
　　图 9： R = 10Ω 且VM = 1V时二极管两端压降的正确趋势