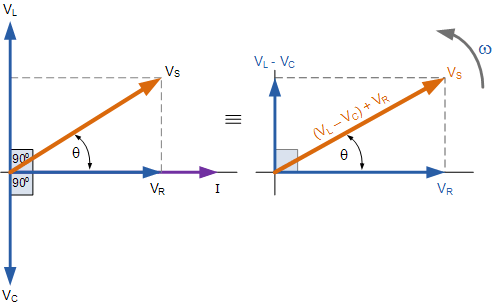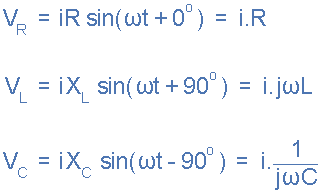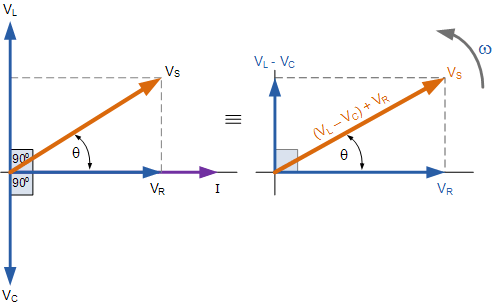
从上面右侧的相量图中我们可以看到，电压矢量产生一个矩形三角形，由斜边V S、水平轴V R和垂直轴V L  – V C  希望您会注意到，这形成了我们的人们喜欢电压三角形，因此我们可以使用毕达哥拉斯定理来计算电压三角形，以数学方式获得V S的值，如图所示。

    串联 RLC 电路的电压三角形

    串联 RLC 电路的电压三角形
    请注意，使用上述等式时，终无功电压必须始终为正值，即必须始终从电压中减去电压，我们不能将负电压添加到 VR 上，因此正确的是有V L  – V C 或  V C  – V L。取值中的值，否则V S的计算将不正确。    从上面我们知道，串联 RLC 电路的所有组件中的电流具有相同的幅度和相位。那么各个元件两端的电压也可以根据流过的电流进行数学描述，而各个元件两端的电压为。

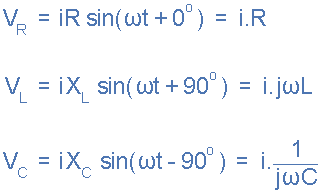
    串联 RLC 电路的瞬时电压    通过将这些值代入上面的电压三角形毕达哥拉斯方程，我们将得到：

    源电压方程
    所以我们可以看到，源电压的幅值与流过电路的电流的幅值成正比。这个比例常数称为电路的阻抗，它终取决于电阻以及感抗和容抗。
    那么在上面的串联 RLC 电路中，可以看出，电流的阻力由三个分量组成，X L、X C和R以及电抗，任何串联 RLC 电路的X T定义为：X T  = X L  – X C 或  X T  = X C  – X L  以较大者为准。因此，电路的总阻抗被认为是驱动电流通过它所需的电压源。