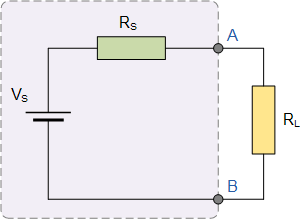
在上面的戴维宁等效电路中,功率传输定理指出“如果负载电阻的值等于供电网络的戴维南或诺顿源电阻,则功率将在负载电阻中耗散”。
换句话说,导致功耗的负载电阻的值必须等于等效戴维南源电阻,则R L = R S但如果负载电阻的值低于或高于网络的戴维南源电阻,其耗散功率将小于值。
例如,找到负载电阻R L的值,它将在以下电路中提供功率传输。 功率传输示例 No1
功率传输定理其中:
R S = 25Ω
R L在 0 – 100Ω 之间变化
V S = 100v
然后使用以下欧姆定律方程:
功率传输
我们现在可以完成下表来确定电路中不同负载电阻值的电流和功率。
电流与功率对照表
电阻L (Ω)我(安培)P(瓦)
04.00
53.355
102.878
152.593
202.297
电阻L (Ω)我(安培)P(瓦)
252.0100
301.897
401.594
601.283
1000.864
使用上表中的数据,我们可以绘制负载电阻、R L与功率、P不同负载电阻值的关系图。另请注意,开路(零电流条件)和短路(零电压条件)时功率为零。
功率与负载电阻关系图
负载功率
从上表和图表中我们可以看到,当负载电阻R L的值等于源电阻 R S 时,功率传输发生在负载中,即:R S = R L = 25Ω 。这称为“匹配条件”,并且作为一般规则,当外部设备的阻抗与源的阻抗完全匹配时,功率从有源设备(例如电源或
电池)传输到外部设备。
阻抗匹配的一个很好的例子是音频
放大器和
扬声器之间的阻抗匹配。放大器的输出阻抗Z OUT可以被给定为4Ω到8Ω之间,而扬声器的标称输入阻抗Z IN可以仅被给定为8Ω。
然后,如果8Ω扬声器连接到放大器输出,则放大器会将扬声器视为8Ω负载。并联两个8Ω扬声器相当于放大器驱动一个4Ω扬声器,并且两种配置均在放大器的输出规格范围内。
不正确的阻抗匹配会导致过多的功率损耗和散热。但是,如何才能使阻抗非常不同的放大器和扬声器进行阻抗匹配呢?嗯,有扬声器阻抗匹配
变压器可以将阻抗从4Ω更改为8Ω,或更改为16Ω,以允许以各种组合连接在一起的许多扬声器进行阻抗匹配,例如在 PA(公共广播)系统中。

