确定三角形连接发电机中的相电压和线电压及电流

　　三相发电机产生的输出电压电平取决于三个独立发电机回路（或线圈）的连接布置。两种可能的连接方法是 wye （Y） 和 delta （Δ），因为电路与这些符号相似。
　　输出电压和电流
　　作为 Y 型连接的替代方案，三相发电机的各个线圈可以以 Δ （delta） 配置连接。
　　在图 1 所示的 Δ 连接发电机中，线圈端子连接 A 到 c，B 连接到 a，C 连接到 b。三条输出线标识为 A、B 和 C。不涉及中性导体。
　　线路电压 （VL） 是测得的电压 E血型、 E公元前或 ECA.下标的顺序表示当每条线路电压为正时端子极性。相电压 （Vp） 是在三个线圈的输出端子上测得的 RMS 电压。
　　从图 1 中可以明显看出，在 Δ 连接的发电机中，线电压和相电压是相同的。对于 Δ 连接的发电机
　　线路电压 = 相电压
　　那是

　　\（V_{L}=V_{P}\） （1）

　　图 1.对于 Δ 连接的三相发电机，相电压和相电流是每个线圈的输出电压和电流。线路电压是在任意两条输出线路之间测得的电压，线路电流是线路中流动的电流。图片由 Amna Ahmad 提供
　　线路电流 （IL） 是在每个线路导体中测得的电流电平。I 指示的方向L每条线路中是线路电压为正时电流流动的方向。
　　当 E血型为正，则线 A 相对于线 B 为正。线路电流 I 的方向一个然后离开端子 A，如图 1 所示。同样，当 B 相对于 C 为正时，IB从端子 B 流出，当 C 比 A 更正时，I 的方向C远离航站楼 C。
　　相电流 （Ip） 是三个发电机线圈中每个线圈中产生的电流水平。
　　同样，图 1 中指示的电流方向是每个线圈输出为正时出现的电流方向。当 E机 管 局为正，则 I一个流出终端 A 并进入终端 A。当 EBb（黑）为正，则 Ib线圈内的方向是从 B 到 B。同样，对于 E抄送，Ic 从 c 流向 C，因此输出电流从端子 C 流出并进入 c。
　　相电流的方向如图 1 所示，环流似乎可能会绕过 Δ 连接的发电机的线圈。这是不可接受的，因为它会在发电机线圈中产生不必要和浪费的功率耗散。
　　考虑下图中的波形，并注意在 t1:
　

eAa=Em<br>

和

eBb=?0.5Em<br>

eCc=?0.5Em

图 1-1。 三相波形。图片由Amna Ahmad提供

 

这些瞬时电压电平可以通过计算轻松确定，如下所示：

eAa=EmSin=EmSin90°=Em<br>

eBb=EmSin(?120°)=EmSin(90°?120°)=?0.5Em<br>

eCc=EmSin(90°?240°)=?0.5Em<br>

 

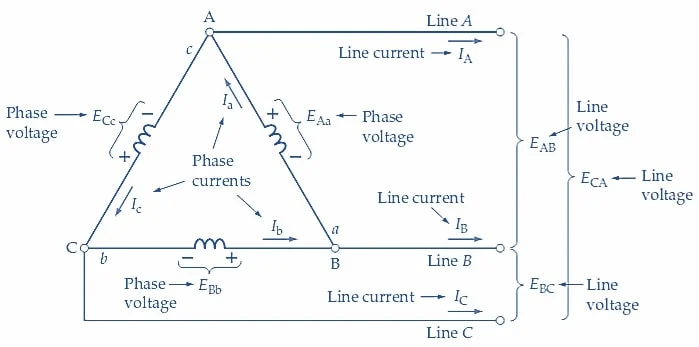
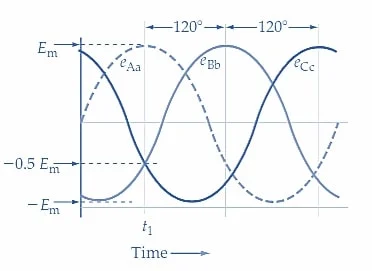
产生循环电流的瞬时电压水平如图 1 所示：

e=eAa+eBb+eCc<br>

 在图 1-1 中的时间 t 1处，

e=Em?0.5Em?0.5Em=0<br>

可以看出，在时间t 1 时， 线圈形成的闭环周围没有电压作用。因此，线圈中没有电流循环。

通过图 1-1 所示的三相波形中的任何其他实例，可以证明在 Δ 连接的发电机中环流电流始终为零。

再次参见图 1，请注意，Ia 流向端子 A，而 Ic 和 IA 均从 A流出 。

这给出了，

Ia=IA+Ic<br>

或者，线电流为，

IA=Ia?Ic

　　因为电流是相量;这是一个 Phasor 差异。
　　图 2（a） 显示了三相发电机在平衡负载下可能产生的相电流的相量图。如前所述，当出现平衡负载时，所有三个线路电流都相等，并且与各自的线路电压具有相同的相位关系。如果负载由三个相等的 Δ 连接电阻组成，则存在平衡负载条件。

　　在图 2（a） 中，三个相等相电流 （I一个我b和我c） 以 120° 相位角间隔绘制。线路电流 I一个如图 2（a） 所示，其中 （I一个-我c）（如前面的方程式中确定）。由此可见，我一个和 –Ic相隔 60°，并且因为它们的星等相等。　IA=Iacos30°+Iccos30°=2(Ipcos30°)=1.732Ip=√3Ip　　

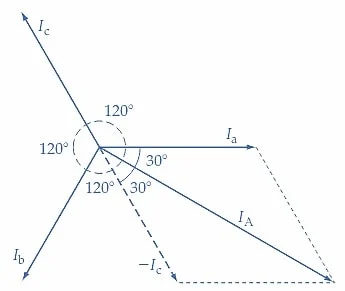
（a） 线路电流 I一个是相量差 I一个-我c

　　（b） 线路电流 IB= 我b-我一个和我C= 我c-我b
　　图 2.对于 Δ 连接的三相发电机，线路电流是相电流对的相量和。在平衡负载下，每条线路电流等于 3（相电流）。图片由 Amna Ahmad 提供
　　因此，在负载均衡的情况下，
　　

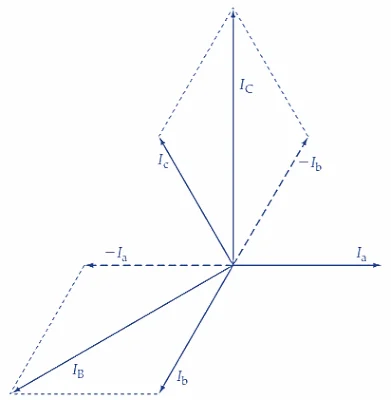
线电流=√3×电流<br>

　　\（I_{L}=\sqrt{3}\times I_{p}\）（2）
　　图 2（a） 还显示（对于平衡负载），相电流 （I一个）引线电流 （I一个） 的 30° 角。在图 2（b） 中，I 的测定B和我C显示为相量差 （Ib-我一个） 和 （Ic-我b） 分别。
　　增量连接载荷

　　用于推导出 Δ 连接发电机的方程 1 和 2 的推理也可以应用于 Δ 连接的负载。对于图3（a）中的电路，各个Δ连接的负载电压显然等于线路电压。

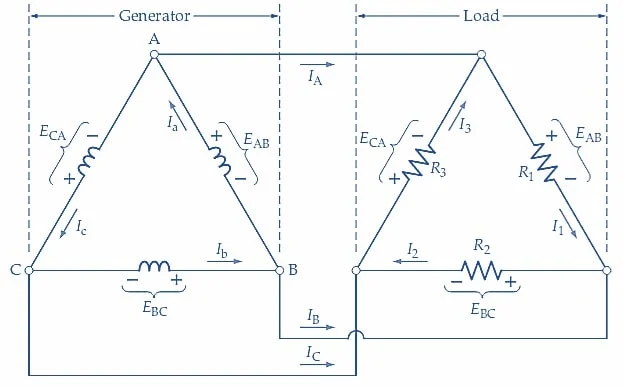
　　（a） Δ 连接电阻负载的 Δ 连接三相发电机

　　（b） 纯电阻负载的负载电压和电流相量图

　　（c） 线路电流 I一个是相量差 I1-我3
　　图 3.具有 Δ 连接平衡负载的 Δ 连接三相发电机的电路和相量图。负载电压等于发电机相电压，线电流为 3（负载电流）。图片由 Amna Ahmad 提供
　

对于 Δ 连接的负载，

负载电压=线路电压负载电压=线路电压

此外，在所有三个负载阻抗相同的情况下，提供平衡负载，各个负载电流组合起来产生，

线路电流=√3×Load电流<br>

实施例1

在图3(a)所示电路中，R 1 =R 2 =R 3 =100 Ω，V p =100 V。计算负载电流和线电流。

解决方案 

根据公式 1，

VL=VP=100V<br>

以电压 E AB 作为所有相角的参考电压，

I1=EABR1=100V100Ω=1A∠0°<br>

I2=EBCR2=100V\角度?120°100Ω=1A\角度?120°<br>

=1A[cos(?120°)+jsin(?120°)]=?0.5A?j0.866A<br>

I3ECAR3=100V\角度?240°100Ω=1A\角度?240°<br>

=1A[cos(?240°)+jsin(?240°)]=?0.5A+j0.866A<br>

负载电压和电流的相量图如图 3(b) 所示。由于负载是纯电阻性的，因此负载电流与负载电压同相。

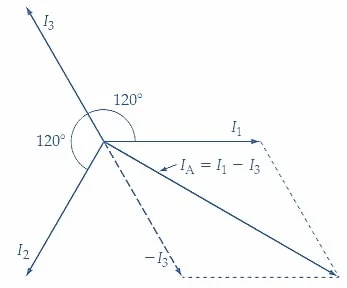
IA=I1?I3=1A?(?0.5A+j0.866A)=1.5A?j0.866A<br>

=√1.52+0.8662∠tan?1(?0.8661.5)=1.732A∠?30°<br>

图3(c)显示了I A的相量推导 为I 1 -I 3。

IB=I2?I1=(?0.5A+j0.866A)?1A=?1.5A?j0.866A

=√1.52+0.8662∠tan?1(?0.8661.5)=1.732A∠?150°

相似地，

IC?I3?I2=(?0.5A+j0.866A)?(?0.54+j0.866A)=0+j1.732A<br>

=1.732A\角度?270°