为什么我们需要与高速 Logic 系列匹配的端接？

电信号在通过电线时具有有限的速度。速度的确切值取决于导线的特性，但我们可以假设其速度大约是光速的一半，接近12×3×10812×3×108米/秒。因此，电信号需要大约 1 纳秒 （ns） 才能通过 15 厘米 （cm） 的电线传播。

信号上升和下降时间

现在，假设我们有一个快速逻辑系列，其上升和下降时间约为 1 ns。如果我们将这个高速 logic 连接到一条相对较长的导线上，这会引入与信号上升时间相当的延迟，会发生什么情况？

正如您可能已经猜到的那样，在这种情况下，我们可能无法将电线视为理想的零延迟导体。事实上，logic gate 可能会将电压转换应用于导线的开头，而导线的另一端仍然具有其先前的电压值。这种现象会给我们带来麻烦吗？我们将在本文后面回答这个问题。首先，我们将讨论传输线。

传输线

当我们处理高速信号时，我们通常需要从传输线而不是普通电线的角度来考虑。传输线需要特殊的分析技术，并且要更加注意导体和接地屏蔽之间的距离或 PCB 走线的尺寸等细节。传输线可以按如下方式建模：

图 1. 点击放大。

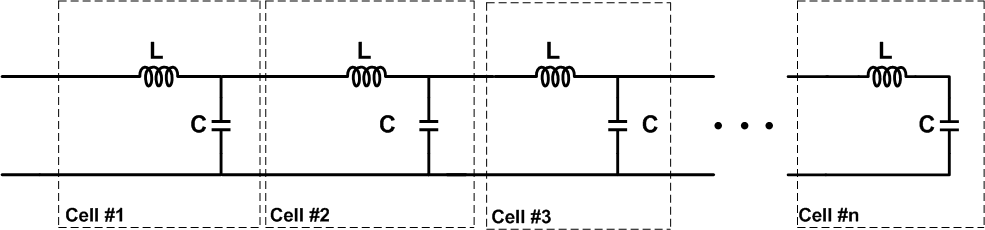
传输线被分成更小的部分，每个部分都使用一些无源元件进行建模。如图所示，这些无源元件沿导线分布。在这里，R 和 G 分别代表导线的电阻和分隔导体的电介质的电导。L 和 C 代表传输线的电感和电容。

请注意，传输线的分布式元件模型通常使用无限系列的单元，如下图 2 所示。

图 2. 用于对传输线进行建模的单元原理图。图片由Omegatron提供 [CC BY-SA 3.0]

在图 2 中，分量 R、L、G 和 C 的值是按单位长度指定的。但是，在图 1 所示的模型中，分量的值不是每单位长度。在图 1 中，我们假设给定长度的传输线被分成足够小的段（或者等效地，n 足够大），以便每个段都可以由一些无源元件表示。使用这个模型，我们将直观地了解传输线中的电波反射。为了简化本文的讨论，我们假设 wire 是无损的 （R = G = 0）。这将得到图 3 所示的模型。

图 3. 点击放大。

如上所述，我们打算基于无损传输线的电路模型来发展对反射现象的直观理解。虽然下面给出的波形的整体形状可以通过电路仿真来验证，但从电路仿真器获得的波形（示例在文章末尾给出）与本主题的更多理论讨论中提供的简化图之间可能存在差异。但是，本文的主要目标不是讨论确切的波形;相反，我们想通过用电路模型替换传输线来解释电波反射。

现在，让我们使用图 3 中的模型来检查将高速逻辑门连接到相对于信号上升时间较长的导线。

无限长的传输线

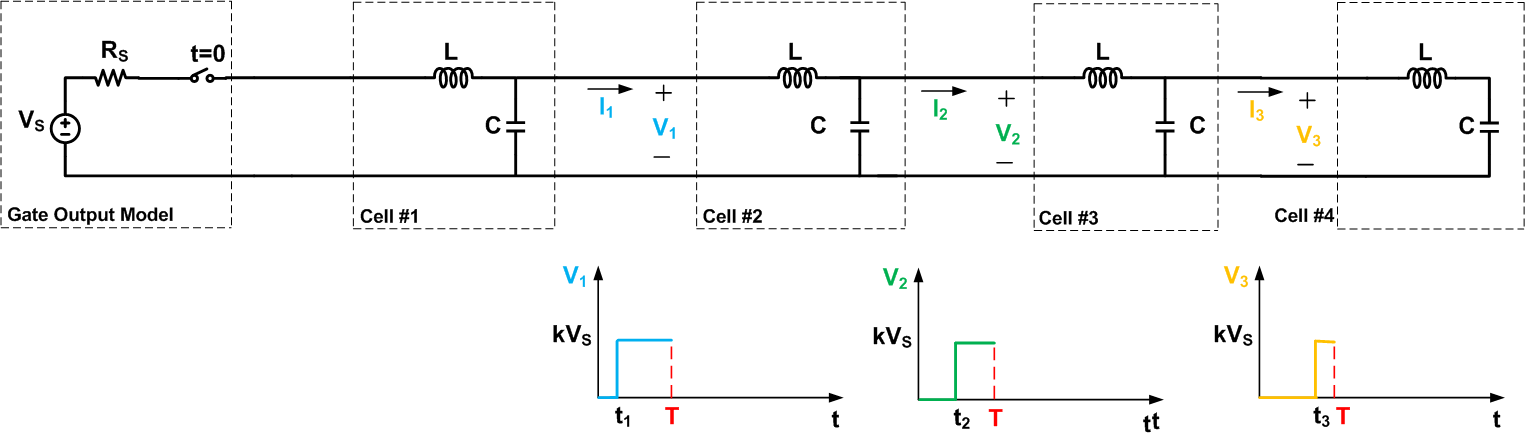
首先，假设 gate 连接到无限长的传输线。图 4 显示了从低到高的转变模型。在此图中，Rs 是从逻辑低电平到逻辑高电平时栅极的输出阻抗，Vs 是逻辑高电压。在本文中，我们将假设栅极的输出电阻 Rs 等于√LCLC。本文末尾将解释此假设的原因。

图 4. 点击放大。

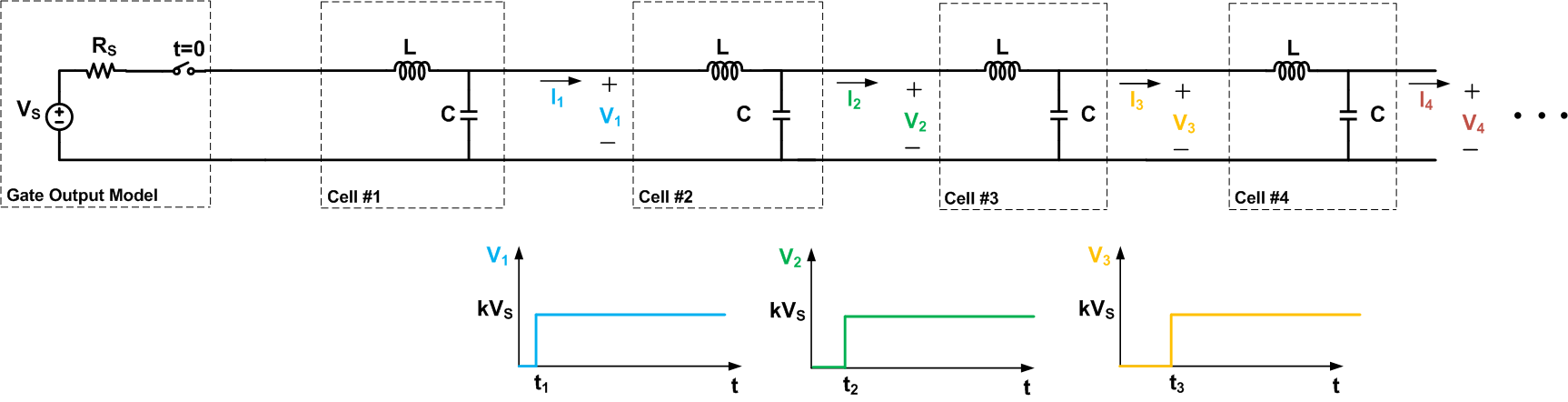
在图 4 中，我们假设了从低到高的非常突然的转变。该图显示，沿线路较远的单元格经历更大的延迟，即t3t3 > t2t2 > t1t1。另外，请注意，当输入源应用从 0 到 Vs 的转换时，电池的电压转换是从 0 到 kVs！因子 k 小于 1;我们不会进行推导值所需的数学运算。

我们假设这条线是无限长的。因此，导线上总有一个电池尚未经历电压转换。导致该特定电池转换的电流必须由放置在导线开头的电压源提供。该电流必须流经更靠近源极的电池，并终输送到经历电压转换的电池。由于电流从源流向导线，我们可以得出结论，电池两端产生的电压小于 Vs（即 k<1）。

可以证明因子 k 等于Z0Z0+RSZ0Z0+RS，其中Z0Z0是传输线的特性阻抗。特性阻抗由传输线的几何形状和材料决定，对于均匀的线路，不取决于其长度。

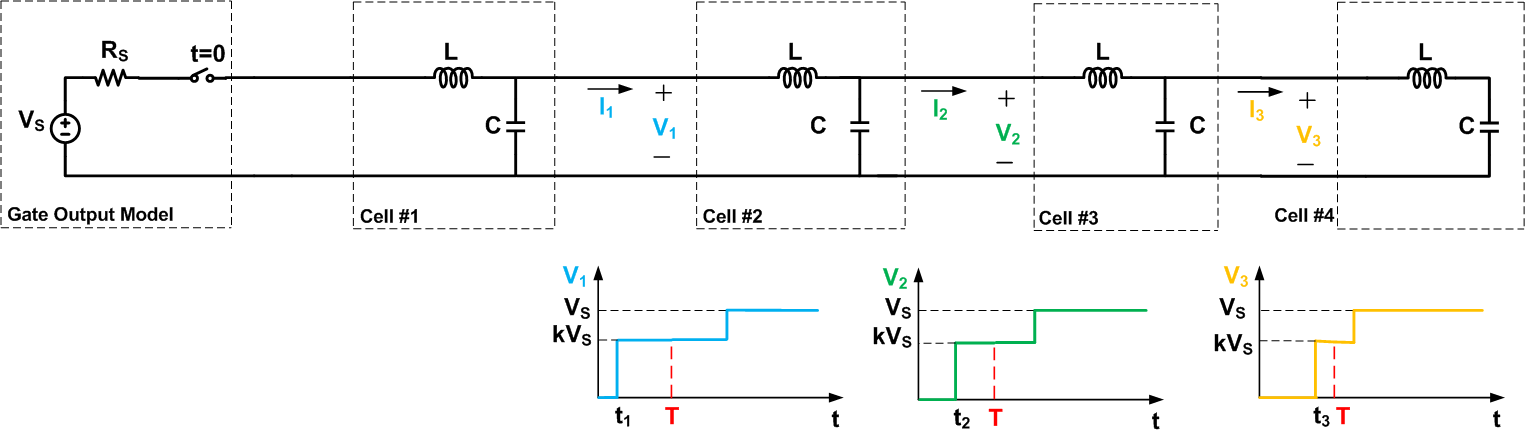
现在我们已经熟悉了电波通过无限长的导线传播，让我们看看沿短路传输线的传播，如图 5 所示。为了简化我们的讨论，我们在图中只显示了四个单元格。

图 5. 点击放大。

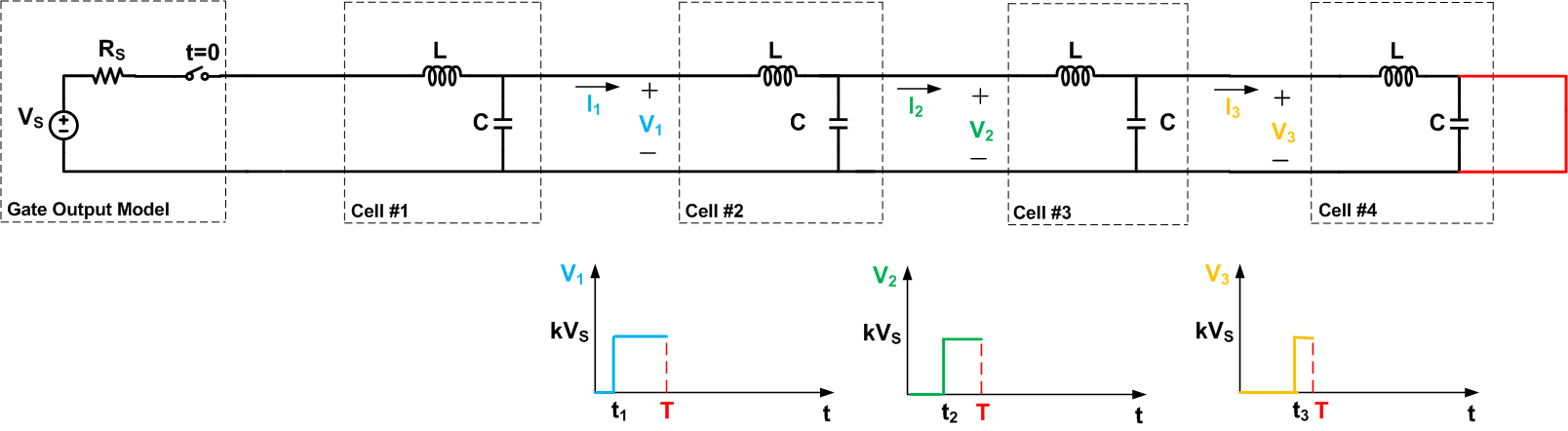
该图显示了tt<T的波形，其中 T 是从传输线起点到其远端的延迟，该远端被红线短路。对于 $t < T$$，图 5 和图 4 的波形是相同的。事实上，在这个区间内，短路会迫使图 5 的第四个电池两端的电压为零，但请注意，该电压初在图 4 中被假定为零。

然而，对于t>Tt>T，两条电路表现出不同的行为。在图 5 中，第四节电池的输出被迫保持在零伏。短路实际上也为以前的电池放电提供了一条路径。这就是为什么在一段时间后，V3V3将表现出向零的过渡。这反过来会导致V2V2在一段时间后归零。因此，我们得到终波形，如图 6 所示。

图 6. 点击放大。

开路传输线

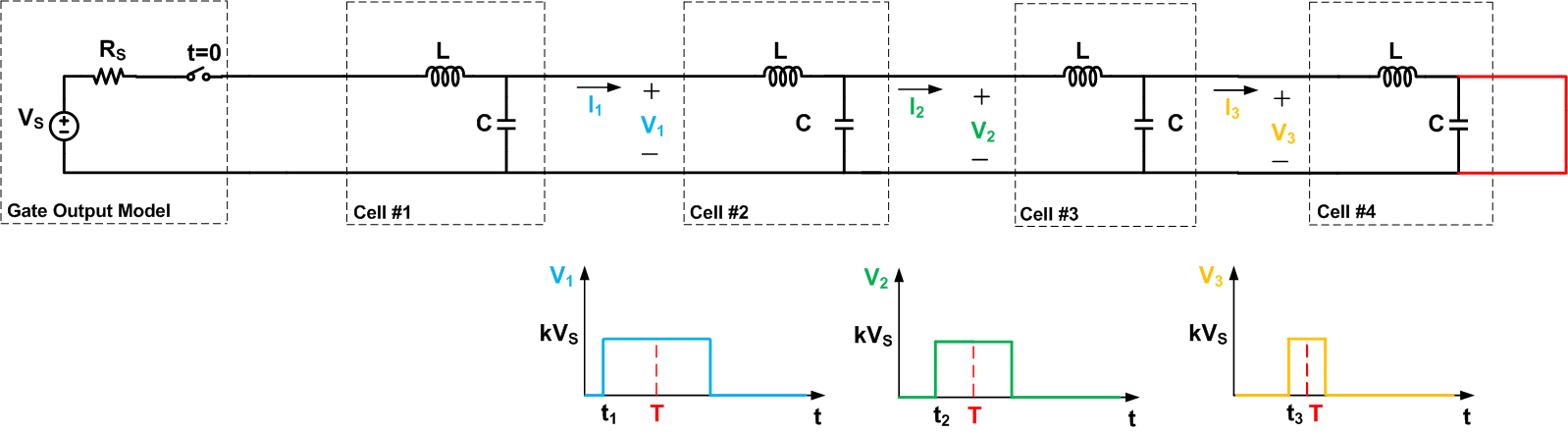
现在，我们来看看电波沿开路传输线的传播，如图 7 所示。同样，为了简化我们的讨论，我们在图中只显示了四个单元格。

图 7. 点击放大。

该图还描述了 t T 的波形，电路显示了不同的行为。由于在第四节电池之后没有任何其他电池，因此一节电池将能够充电到 Vs 而不是 kVs。现在第四节电池充电到源电压，流入该电池的电流将趋于零。这将允许第三个电池充电至 Vs。然后，更靠近源极的其他电池两端的电压将以类似的方式达到 Vs。请注意，靠近传输线末端的信元将经历较短的延迟以达到其终值。完整的波形如图 8 所示。

图 8. 点击放大。

反射系数

为了统一处理这个问题，我们可以定义一个反射系数：

ρ=ZtermZ0Zterm+Z0ρ=Zterm<br>Z0Zterm+Z0

其中ZtermZterm和Z0Z0是传输线的端接阻抗和特性阻抗。例如，考虑图 6 中所示的波形。在这种情况下，终止阻抗为零，得到ρ=?1ρ=?1。这意味着图 5 所示的原始波形将以 -1 的反射系数进行反射。换句话说，幅度等于原始波但极性相反的波将从传输线的短路端反射。

对于图 8 的波形，终止阻抗是无穷大的，得到ρ=1ρ=1。因此，等于原始波的波将从传输线的开路端反射。将反射波形添加到原始波形中，可以得到图 8 所示的波形。

避免反射

上面的讨论显示了端接传输线的电阻的重要性。从示例中可以看出，不同的终端电阻会导致不同的反射系数。我们如何避免反射？

我们观察到，当传输线为无限长时，没有反射。在实践中，我们不能有无限长的传输线，但我们可以使用等于线路特性阻抗的端接电阻来避免反射。这也可以使用等式 1 来验证，该方程式给出Zterm=Z0Zterm=Z0的ρ=0ρ=0。例如，当正参考射极耦合逻辑 （PECL） 通过传输线驱动负载时，我们将传输线端接到接近线路特性阻抗的电阻。如图 9 所示。

图 9.Thevenin 端接，用于驱动 50 传输线的 PECL 栅极。图片由 idt 提供。

在图 9 的示例中，终止电阻为R1||R2=50ΩR1||R2=50Ω等于线路的特性阻抗。值得注意的是，除了提供匹配的端接外，电阻器的值还决定了 PECL 接收器输入的直流电平。在本例中，选择电阻器将输入的 DC 电平设置为约 1.3V。

在上面的例子中，我们看到当ZtermZterm不等于Z0Z0时，传输线的末端可以反映传播波。需要注意的是，如果源电阻 Rs 不等于Z0Z0，则当到达传输线的起点时，反射波本身可以被重新反射。由于无损传输线的特性阻抗等于√LCLC，因此我们在文章开头假设了Rs=√LCRs=LC，以避免反射波的重新反射。

如果 logic gate 的上升时间长于 2T，其中 T 是导线的延迟，那么我们可以忽略反射。在这种情况下，反射返回，而输入仍在上升，因此我们将有一个稍微减慢且“颠簸”的上升沿，但整体功能会很好。

一些模拟

在前面的部分中，我们使用电路模型来检查沿传输线的电波反射。现在，我们将看看从电路仿真中获得的一些波形。在这些仿真中，我们级联了 20 个 LC 单元来模拟假设的传输线。与图 5 所示的原理图类似，传输线的末端短路。从低到高的过渡应用于此传输线的起点。在图 10 所示的个仿真波形中，我们选择了 L = 2.5 nH 和 C = 1 pF。在此图中，红色曲线是施加到传输线输入端的脉冲，蓝色曲线是在第 10 节电池输出端观察到的电压。如您所见，起初，我们有一个从低到高的过渡。然后，经过一段时间的延迟后，波形表现出从高电平到低电平的过渡。这与我们为图 5 获得的波形一致。然而，与图 5 的波形不同，图 10 中有一些振铃行为。

图 11. L = 2.5 nH 和 C = 1 pF 的短路传输线模型的仿真波形。点击放大。

现在，我们将 L 和 C 的值更改为 0.05 nH 和 0.02 pF。在这种情况下，波形如图 11 所示。

图 11.L = 0.05 nH 和 C = 0.02 pF 的短路传输线模型的仿真波形。点击放大。

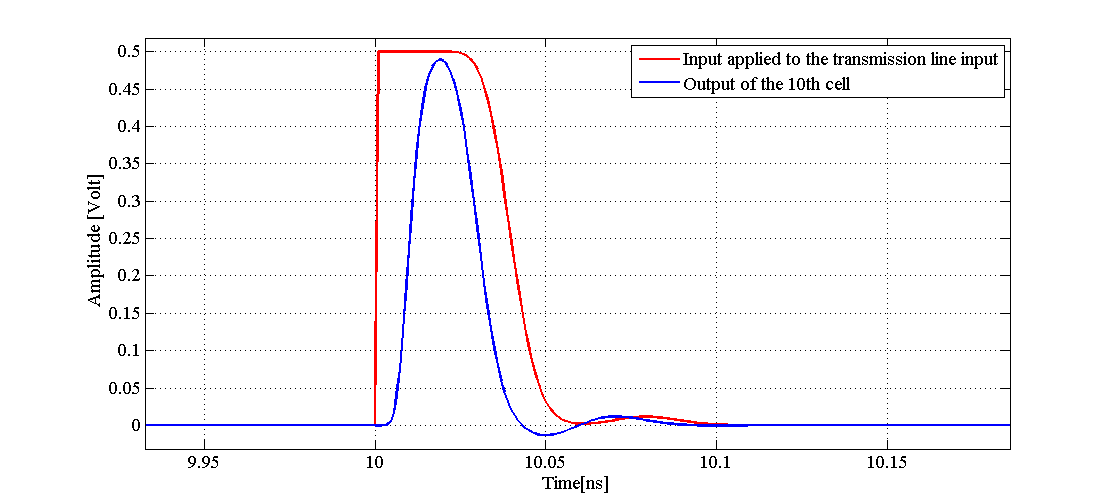
将图 10 与图 11 进行比较，我们观察到可能存在也可能不存在振铃效应，但整体行为如本文所述：远端有短路线路，由于波反射现象，电压波形返回为零伏。