本文将回顾用于设计有限脉冲响应 (FIR) 滤波器的频率采样方法的基础知识。
与无限脉冲响应 (IIR) 滤波器相比,FIR 滤波器有两个主要优点:
本文将教您如何使用频率采样方法设计 FIR 滤波器。
假设我们要设计一个具有所需频率响应 Hd(ω) 的有限脉冲响应 (FIR) 滤波器。窗口方法应用逆离散时间傅立叶变换来查找相应的时域表示 hd(n),如下所示
hd(n)=12π∫π?πHd(ω)ejnωdω
一般来说,hd(n) 的长度不是有限的,并且由于我们正在寻找有限的脉冲响应,因此我们可以截断 hd(n) 并获得所需的近似值回复。这相当于将 hd(n) 乘以矩形窗口。
正如前一篇文章《 从 FIR 滤波器设计中的滤波器规格到窗口参数》中所讨论的,我们可以使用其他窗口函数来实现通带纹波和过渡带锐度之间的权衡。
对于许多经典滤波器,我们可以轻松计算公式 1 的积分。例如,假设我们正在设计一个截止频率为 ωc 的理想低通滤波器。那么,我们有
H_d(\omega)=\begin{情况}1 & |欧米茄| \leq \omega_c \\0 & else\end{}
在这个特定的例子中,一些数学运算可以很容易地引导我们得到相应的hd(n)因为Hd(ω)是由一个简单的方程给出的。然后,我们可以应用合适的窗函数来获得有限长度响应,这是所需滤波器的近似值。
然而,如果Hd(ω)有一个复杂的方程,我们将无法轻松计算方程1。在这些情况下,我们可以使用频率采样方法来设计具有任意Hd的FIR滤波器(ω)。
在本文中,我们将首先回顾一个实际示例,其中所需的 FIR 滤波器具有复杂的频率响应,而频率采样方法非常有帮助。然后,我们将回顾使用此方法设计 FIR 滤波器的基础知识。
我们可以将实用的 DAC 视为理想的 DAC,它产生脉冲序列,后跟零阶保持块。

之所以需要保持电路,是因为实际上我们无法产生理想 DAC 的窄脉冲。然而,在理想 DAC 的输出处放置零阶保持(如图 1 所示)意味着理想输出 ys(t) 将通过保持电路的传递函数进行修改。可以证明零阶保持的传递函数为
H(f)=thsin(πfth)πfth
其中 th 是保持时间,通常等于采样周期。下图显示了保持电路的归一化频率响应,即HDAC=H(f)th

如上图所示,与低频分量相比,fs2 附近的频率分量经历了约 4 dB 的衰减。我们在之前关于 D/A 转换中的多速率 DSP 的文章中讨论过 ,可以采用多速率系统来缓解该问题。然而,对于相对较小的过采样率值(例如,L≤8),我们可能仍然需要补偿保持电路失真。为此,我们可以对图 1 中的 y(n) 应用频率响应为 1HDAC 的滤波器。
假设我们使用多速率系统(参见图 3),我们可以修改插值滤波器本身以避免使用额外的滤波器。在这种情况下,插值滤波器响应的幅度将与滤波器通带中的 1HDAC 成正比 (0≤ω≤πL 表示 L 倍插值),否则为零。

总而言之,我们可以使用公式 1 来设计理想的滤波器,例如公式 2 给出的滤波器。但是,当设计具有任意频率响应的滤波器时,例如当设计 H(z的幅度时),这种方法并不容易。) 等于特定频段中的 1HDAC。在这些情况下,我们可以使用频率采样方法。
频率采样方法基于用近似和代替方程 1 的积分。假设我们需要设计一个频率响应如图 4 所示的滤波器。

为了得到更简单的数学表达式,我们可以使用下图中的红色曲线来近似H(ω)
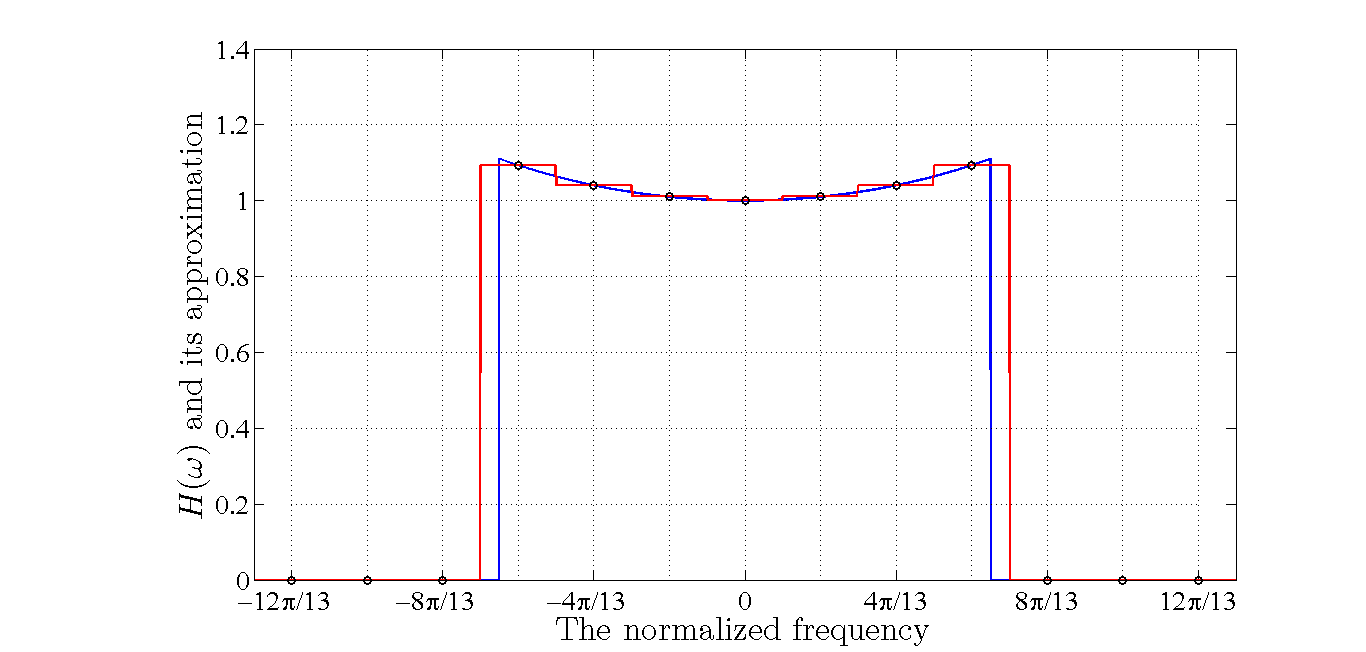
在此特定示例中,以规则频率间隔 2π13k 对所需频率响应进行采样,其中 k=0,1,2,…,12 (样本图中用点表示)。如果我们要计算 H(ω) 本身的积分,我们可以简单地近似计算红色曲线下面积的积分,该面积是 13 宽度为 2 的矩形之和pi13 和长度由 H(ω) 的样本确定。为了执行方程 1 的积分,我们还需要考虑 ejnω 项。因此,对于 H(ω) 的 N=2M+1 样本,我们可以使用公式 1 来近似
h_{d}(n)=\frac{1}{2\pi} \left ( \sum_{k=-M}^{M}H(\omega_k)e^{jn\omega_k}\frac{ 2\pi}{2M+1} \右 )
其中ωk=2π2M+1k
上式中,H(ωk)ejnωk和2π2M+1分别表示用于近似的矩形的长度和宽度H(ω)ejnω。有趣的是,将本文关于 DSP 中的 DFT 分析的公式 3 与公式 2 进行比较,我们发现频率采样方法实际上是计算 H(ω) 样本的离散傅里叶逆变换。
我们可以通过考虑频率响应关于原点对称的情况来进一步简化方程 3,即 H(ωk)=H(ω?k)。因此,我们得到
小时d(n)=12中号+1(H(ω0)+中号Σk=1H(ωk)(ejnωk+e-jnωk))
这给出了
小时d(n)=12中号+1(H(ω0)+2中号Σk=1H(ωk)c哦s(nωk))
请注意,在计算$$h_d(n)$$之后,我们可以以类似于上面讨论的加窗方法的方式应用窗口函数。小时d(n),我们可以以类似于上面讨论的加窗方法的方式应用窗口函数。
使用频率采样方法设计一个 9 抽头低通 FIR 滤波器,截止频率为 $$0.25\pi$$ 弧度/样本。0.25π弧度/样本。
首先,我们需要找到频率响应样本的值。假设理想响应,低于 $$0.25\pi$$ 的样本等于 $$1$$,其他样本为零。然后,我们得到0.25π等于1其余样本均为零。然后,我们得到

因此,方程 4 给出
小时d(n)=19(1+2c哦s(2π9n))
根据该方程,我们得到相应的时域表示,如下表所示:

设计的滤波器的频率响应如图6所示。

该图显示设计的滤波器的通带和阻带中存在一些纹波。这些纹波使得获得的响应偏离目标理想滤波器的响应。然而,请注意,在 $$\tfrac{2\pi}{9}k$$, $$k=0, 1, \dots, 8$$ 处,滤波器准确地表现出了我们初寻找的幅度响应(见表1)。这可以通过注意到频率采样基于逆 DFT 分析来解释。我们将逆 DFT 应用于表 1 的频域样本,并获得相应的时域序列 $$h_d(n)$$。图 6 是 $$h_d(n)$$ 的频率内容及其在 $$\tfrac{2\pi}{9}k$$, $$k=0, 1, \dots, 8 处的等距样本$$ 给出 $$h_d(n)$$ 的九点 DFT。显然,这些样本应该与表 1 中给出的样本相匹配。2π9k,k=0,1,……,8,滤波器准确地展现了我们初寻找的幅度响应(参见表 1)。这可以通过注意到频率采样基于逆 DFT 分析来解释。我们对表1的频域样本应用逆DFT,得到相应的时域序列,小时d(n)。图6是频率内容小时d(n)及其等距样本2π9k,k=0,1,……,8给出九点 DFT小时d(n)。显然,这些样本应该与表 1 中给出的样本相匹配。
我们可以增加频域样本的数量,以获得更好的目标滤波器近似值并实现更清晰的过渡。显然,这将需要更高阶的滤波器。下一个示例解释了示例 1 的低通滤波器的 25 抽头滤波器的设计。
使用频率采样方法设计一个 25 抽头低通 FIR 滤波器,其截止频率为 $$0.25\pi$$ 弧度/样本。0.25π弧度/样本。
首先,我们找到频率响应样本的值。假设理想响应,$$0.25\pi$$ 以下的样本等于 $$1$$,其他样本为零。然后,我们得到0.25π等于1其余样本均为零。
和
因此,方程 4 给出
小时d(n)=125(1+2(c哦s(2π25n)+c哦s(4π25n)+c哦s(6π25n)))
根据该方程,我们得到相应的时域表示,如下表所示:

和

所实现的 25 抽头滤波器的频率响应如图 7 所示。

为了减少通带纹波,我们可以采用窗函数;然而,这会增加过渡带,我们可能需要进一步增加滤波器长度以实现更清晰的响应。
当$$H_d(\omega)$$由一个简单的方程给出时,我们可以很容易地计算方程1的积分。然而,对于任意的$$H_d(\omega)$$,频率采样方法会更容易申请。Hd(ω)由一个简单的方程给出,我们可以很容易地计算方程 1 的积分。然而,对于任意Hd(ω),频率采样方法会更容易应用。
对于相对较小的过采样率值(例如,$$L \leq 8$$),我们可能需要补偿保持电路失真。为此,我们可以设计插值滤波器,使其频率响应为$$\tfrac{1}{H_{DAC}}$$。L≤8),我们可能需要补偿保持电路失真。为此,我们可以设计插值滤波器,使其频率响应为1HD一个C
。
对于$$H(\omega)$$的$$N=2M+1$$个样本,我们可以使用公式4确定频率采样方法的滤波器系数。氮=2中号+1的样本H(ω),我们可以使用公式 4 确定频率采样方法的滤波器系数。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。