DSB-SC 调制:综述
在我们开始之前,让我们快速回顾一下 DSB-SC 调制。在这种方法中,调制信号 (s(t)) 是通过将消息信号 (m(t)) 乘以载波 c(t 来产生的)) = 一个c余弦(Ωct): s(t) = m(t) × 一个c因为(ωct) 方程 1.
在频域中,m(t) 乘以载波对应于基带信号频谱 M(f) 与余弦函数频谱的卷积。因此,如图 1 所示,调制波的频谱将具有两个基带频谱副本,一个副本移至fc另一个是——fc.
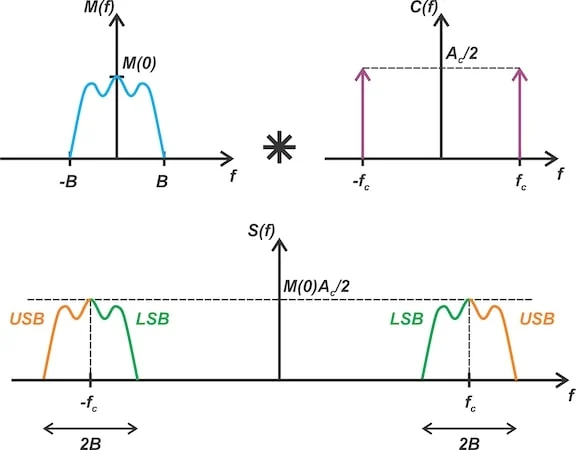
用于 DSB-SC 调制的基带和输出频谱。
图 1.时域中的乘法对应于基带频谱与频域中载波的卷积(上图)。这将基带频谱转换 ±fc(下图)。
这里的关键点是,与正弦载波相关的脉冲函数(由上图中的紫色垂直箭头表示)不会出现在调制信号的频谱中。从功率使用的角度来看,这是有利的,因为载波消耗了相当一部分传输的功率,而没有传达任何有用的信息。正如我们之前提到的,缺点是它会导致
接收器硬件的复杂性增加。
传统的 AM 输出频谱
为了将载波保留在传输的频谱中,我们使用以下公式来生成调制信号:
s(t) ~=~ A_c \Big ( 1~+~ \mu m(t) \Big ) \cos(\omega_c t)
方程 2.
哪里:
一个c是载波幅度
m(t) 是消息信号
μ 是调制指数(一个比例因子)。
在一个c(1 + μm(t)) 导致载波出现在输出频谱内。
图 2 显示了此类幅度调制的典型输出频谱。

基带信号 (a) 和常规调幅信号 (b) 的频谱。
图 2.基带信号 (a) 和常规调幅信号 (b) 的频谱。
比较图 1 和图 2,我们可以看到传输带宽是消息信号 (BT= 2B) 的 DSB-SC 和常规 AM。两种 AM 类型的输出频谱都包括 2 个基带频谱的复制品,其频率由 ±fc.然而,与 DSB-SC 方法不同的是,传统的 AM 谱包括两个由因子 0.5 加权的 delta 函数一个c.
传统 AM 中的调制指数
要讨论时域中的常规 AM,我们首先需要了解调制指数的作用。例如,考虑一条单音消息,m(t) = cos(ωmt),调制载波 c(t) = cos(ωct).图 3 显示了调制指数 μ = 0.8 时的载波和调制波的瞬时幅度 g(t) = 1 + μm(t)。
函数 g(t) 表示 μ = 0.8(上)和正弦载波(下)。
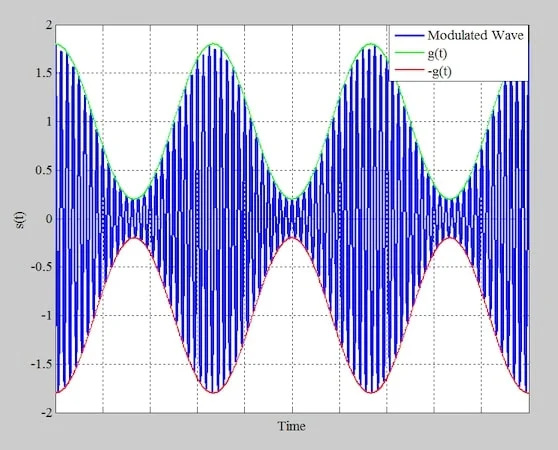
图 3.函数 g(t) 表示 μ = 0.8(上)和正弦载波(下)。
应用公式 2 可生成图 4 中的调制波形。图中的蓝色波形表示调制波;绿色和红色波形分别表示函数 g(t) 和 –g(t)。
调幅波(蓝色)、函数 g(t)(绿色)和 μ = 0.8 的 g(t)(红色)的倒置形式。
图 4.幅度调制波(蓝色)、函数 g(t)(绿色)和 μ = 0.8 的 g(t)(红色)的倒置形式。
您可能还记得上一篇文章对 DSB-SC 调制的讨论,调制信号的包络被定义为连续、平滑的曲线,它跟踪调制波形的瞬时峰值。在上面,调制信号的上包络与函数 g(t) 匹配,而调制波形的下包络是 –g(t)。
函数 g(t) 的形状与 m(t) 相同,只是偏移了一个 DC 值。从 g(t) 中提取 m(t) 需要一个 DC 模块来消除信号的 DC 分量。由于消息信息包含在调制波的包络中,我们可以使用简单的包络
检测器电路来恢复消息。
接下来,图 5 和图 6 说明了当我们将调制指数增加到 μ = 1 时会发生什么。图 5 显示了新值 μ 的调制信号的载波和瞬时幅度。
函数 g(t) 表示 μ = 1(上)和正弦载波(下)。
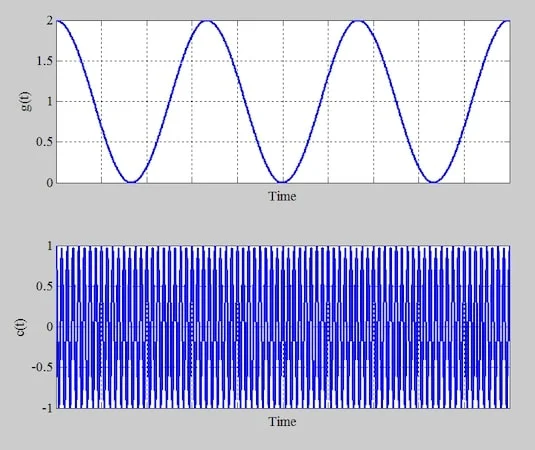
图 5.函数 g(t) 表示 μ = 1(上)和正弦载波(下)。
图 6 显示了调制波形以及 g(t) 和 –g(t)。
调幅波(蓝色)、函数 g(t)(绿色)和 g(t) 的倒置形式(红色),其中 μ = 1。
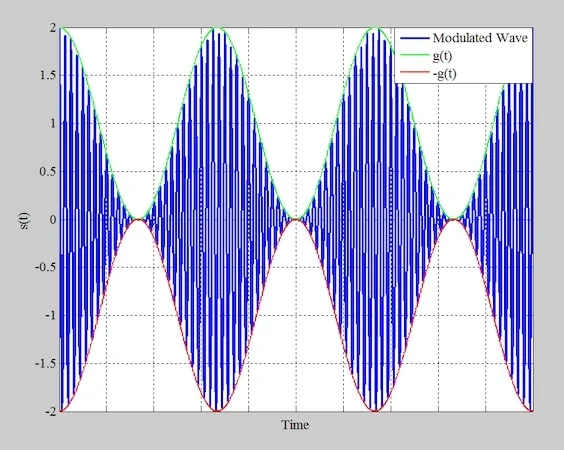
图 6.调幅波(蓝色)、函数 g(t)(绿色)和 g(t) 的倒置形式 (红色),μ = 1。
调制信号的包络再次等于 g(t) = 一个c(1 + μm(t))。当 1 + μm(t) 对于所有 t 值均为正值时,此条件意味着简单的包络检测器可用于解调。
我们通常假设 |m(t)|小于或等于 Unity (|m(t)|≤ 1)。条件 “1 + μm(t) 对所有 t 均为正” 要求 μ 小于 1。为了测试这一点,让我们看看当我们增加 μ = 1.2 时会发生什么。图 7 和图 8 显示了生成的波形。
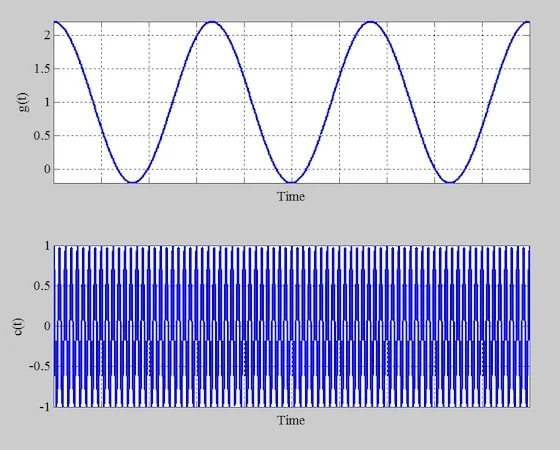
函数 g(t) 表示 μ = 1.2(上)和正弦载波(下)。
图 7.函数 g(t) 表示 μ = 1.2(顶部)和正弦载波(底部)。
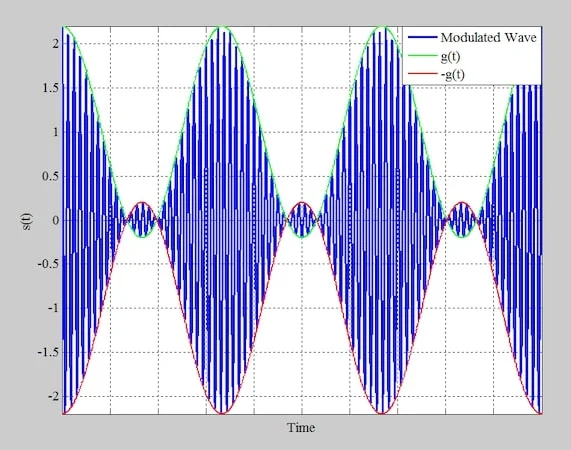
图 8.调幅波(蓝色)、函数 g(t)(绿色)和 μ = 1.2 的 g(t)(红色)的倒置形式。
在图 7 中,我们可以看到函数 g(t) = 1 + μm(t) 对于 t 的某些值为负数。当 g(t) 达到零时,调制波形中会发生相位反转。因此,当 g(t) 为正时,上包络与 g(t) 匹配,但当 g(t) 为负时,上包络将切换到 –g(t)。换句话说,上包络对应于 g(t) 的。当 g(t) 并不总是正时,我们说载流子被过调制。
由于调制波形的包络不再等于 g(t),而是等于 |g(t)|,我们不能使用包络检测器进行解调。相反,恢复消息信号需要一个 synchronous deachator,这要复杂得多。因此,几乎所有商业 AM 电台都以非负 g(t) 传输传统 AM。
在我们继续之前,值得一提的是,载波频率必须远大于消息信号的频率 (fc? B)。如果不是这种情况,接收器将无法检测到包络(跟踪调制波形的峰值)。
传统增材制造的功率效率
鉴于 carrier 不包含任何消息信息,我们可以认为它的功能被浪费了。为了量化传统幅度调制的功率效率,我们将调制信号(公式 2)表示为:
s(t) = 一个c因为(ωct) + 一个cμm(t)因为(ωct) 方程 3.
假设 s(t) 是一个电压量。如果我们将此电压施加在 1 Ω
电阻器上,则传递到
电阻器的平均功率如下: P1Ω = 林T→∞1T∫T/2?T/2s2(t) dt 方程 4.
如果 s(t) 是一个周期性信号,则计算一个周期的积分就足够了。在实践中,s(t) 通常不是周期性的,因此我们需要在更长的时间内进行测量。
等式 5 给出了方阵消息信号的表达式:
$$s^2(t) ~=~ A_c^2 \cos^2 (\omega_c t) ~+~ \big (A_c \mu m(t) \big )^2 \cos^2 (\omega_c t) ~+~ 2 A_c^2 \mu m(t) \cos^2 (\omega_c t)$$
方程 5.
考虑上述方程的一项的时间平均值。应用基本的三角恒等式,我们可以按如下方式扩展余弦函数的平方:
$$\begin{gather*}\lim_{T \rightarrow \infty} \frac{1}{T} \int_{-T/2}^{T/2} 2 A_c^2 \mu m(t) ~\times~ \frac{ 1 + \cos (2 \omega_c t )}{2} \ dt \\=~ A_c^2 \mu ~\times~ \lim_{T \rightarrow \infty} \frac{1}{T} \int_{-T/2}^{T/2} m(t) ~+~ m(t) \cos (2 \omega_c t ) \ dt ~=~ 0 \end{gather*}$$
方程 6.
通常假设 m(t) 的时间平均值为零,从而导致我们上面看到的零结果。
另请注意,两个独立函数的乘积的时间平均值等于它们各自时间平均值的乘积。由于函数 m(t) 和 cos(2ωct) 是独立的,并且 m(t) 的时间平均值为零,则 m(t)cos(2Ω ) 的时间平均值ct) 也计算为零。因此,公式 4 简化为:
$$\begin{eqnarray}P_{1 \Omega} ~&=&~ \lim_{T \rightarrow \infty} \frac{1}{T} \int_{-T/2}^{T/2} A_c^2 \cos^2 (\omega_c t) ~+~ \big (A_c \mu m(t) \big )^2 \cos^2 (\omega_c t) \ dt \\&=&~ \frac{1}{2}A_c^2 ~+~ \frac{1}{2}A_c^2 \mu ^2 ~\times~ \overline{m^2(t)} \end{eqnarray}$$
方程 7.
在上面的方程中,m 上的条形2(t) 表示其时间平均值。虽然项为载波提供功率 (Pc),则第二项量化了承载信息信号分量(边带功率,或Ps).
我们打算传输驻留在Ps.Pc仅用于使解调更方便。基于此,我们现在可以计算 Power Efficiency:
$$\eta ~=~ \frac{P_s}{P_c ~+~ P_s} ~=~ \frac{\frac{1}{2}A_c^2 \mu^2 ~\times~ \overline{m^2(t)}}{\frac{1}{2}A_c^2 ~+~ \frac{1}{2}A_c^2 \mu ^2 ~\times~ \overline{m^2(t)}}~=~\frac{\mu ^2 ~\times~ \overline{m^2(t)}}{1 ~+~ \mu ^2 ~\times~ \overline{m^2(t)}}$$
方程 8.
为了深入了解上述方程,我们假设消息信号是一个单音正弦曲线,由 m(t) = cos(ω 给出)mt).m 的时间平均值2(t) 为 0.5,从而产生: η = PsPc + Ps = μ22 + μ2
方程 9.
公式 9 表明,效率随 μ 的增加而增加。我们知道调制指数 (μ) 需要是一个小于或等于 unity (0 ≤ μ ≤ 1) 的正值。因此,效率出现在 μ = 1 时,等于 η = 33%。
这意味着,对于条件下 (μ = 1) 的单音正弦消息,只有三分之一的发射功率用于传输消息信息。较小的调制指数值会进一步降低效率。例如,当 μ = 0.5 时,效率降低到 11.11%。
电源效率的降低是拥有更简单的接收器硬件的权衡。






