电导率、电阻和欧姆定律

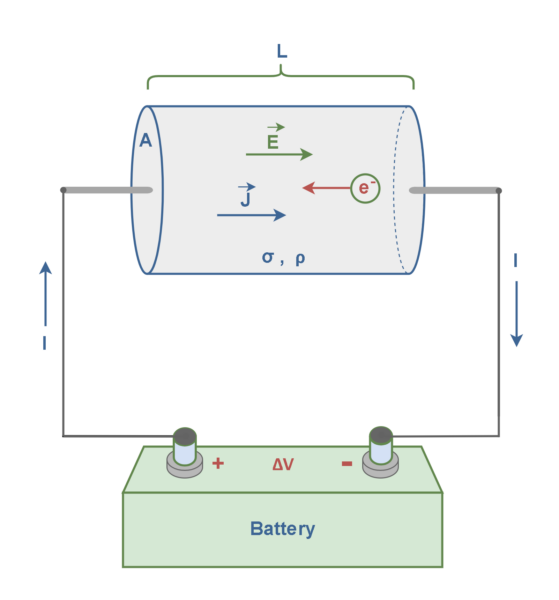
　　考虑一个圆柱形导体，其两端施加电压，如图1所示。当在导体中的两点之间施加电势差（电压 ΔV）时 ，就会产生电场 E，导体中的自由电子 (e – ) 会感受到电场产生的力。这种现象导致自由电荷移动并产生电流。这些电线必须是闭合电路的一部分，以便稳定电流“I”在这个简单电路中的电线中流动。导线中的电流与导体内自由电子的漂移速度成正比。电导率是常用来表征材料电磁特性的主要本构参数之一。关键思想是，电导率是材料的一种特性，决定了响应所施加电场的传导电流密度 (J)。

　　图 1：两端施加电压 ΔV 的金属导电圆柱体图 1：两端施加电压 ΔV 的金属导电圆柱体

　　德国物理学家Georg Simon Ohm于 1827 年首次总结了这一实验关系。方程 1（称为电磁学欧姆定律）指出，电流的体积密度等于电导率乘以电场强度：

　　方程 1：以电导率和电场表示的电流密度方程 1：以电导率和电场表示的电流密度
　　式中，E为电场强度（V/m）；J为描述电流流动的电流密度矢量，单位为安培/m 2； “σ”是电导率。在此公式中，σ 的单位为mho s每米 (Ω -1 m -1 )。姆欧（电阻单位ohm 1 Ω -1的倒数）是电导的旧术语，至今仍在使用。该装置于 1971 年采用新名称，以纪念 德国电气工程师、发明家和实业家恩斯特·沃纳·冯·西门子（Ernst Werner von Siemens ，1816 年至 1892 年）。那么，σ 更常见地表示为西门子每米或 S/m。公式 1中解释的概念提供了电导率的宏观观点，电导率本质上是衡量材料允许电流流动的能力的指标。值得注意的是，这里讨论的电流是传导电流，而不是任何其他形式的电流。
　　导体和绝缘体

　　电导率 (σ) 作为一种电磁特性，取决于材料内真实电荷的可用性和迁移率。材料根据其电导率 σ 可以分为几类。以下是经常遇到的几类材料：完美的绝缘体；完美的真空或自由空间不包含电荷（在没有材料的情况下），因此它是 σ = 0 的完美绝缘体。绝缘体良好；通常具有 σ << 10 -10 S/m 的电导率，该电导率足够低，通常可以忽略所产生的电流。熟悉的例子是空气，它的电导率仅略大于自由空间的电导率。一类重要的良好绝缘体是无损 电介质，其仅用相对介电常数(? r )就可以很好地表征，并且通常可以假设 σ = 0。绝缘体不良；其电导率较低，但产生的电流不容忽视。这些有损 电介质可以用 r和 σ 来表征。半导体；是主要用于晶体管和集成电路的材料，具有中等电导率，通常约为 10 +1 S/m。尽管半导体中的电流类型是传导电流，但其行为及其背后的机制与金属中的电流有很大不同。良导体；是具有非常高电导率的材料，通常大于10 5 S/m。良导体是一种含有可在材料内自由移动的电荷（电子）的材料。当电场施加到良导体时，电荷沿电场确定的方向移动，从而在该方向产生电流。一类重要的良导体包括金属，其中某些金属（包括铝、铜、银和金的合金）的电导率达到10 7 S/m的量级。这种材料中没有大量的能量存储，因此相对介电常数 (? r ) 的概念与良导体无关。它们通常用于布线和电气元件。完美导体；是其中 σ → ∞、E → 0 的材料。金属通常被建模为完美传导等势体积以简化分析。在上述分类中，在两个极端，我们有完美绝缘体（σ = 0）和完美导体（σ → ∞）。一些特殊材料接近这些极端条件，而大多数其他材料则介于这些条件之间。一些常见材料在20℃温度下的电导率值列于表1。

　　表1：不同材料的电导率，单位为西门子每米

　　图 2(a)显示了基于包含电池、一些电线和两个电极的简单电路的测试结构。如果我们在两个正电极和负电极之间放置一块导电材料（如金属棒），由于电势差和电子的运动，电流“I”将在所有电路中流动。电流量取决于电压 ΔV 和被测材料的电导率。

　　图 2 (a)：两个相反极性电极之间的导电材料图 2 (a)：两个相反极性电极之间的导电材料

　　图 2(b)显示了相同的结构，但在 2 个正电极和负电极之间有一块非导电材料（如木棒）。这里，虽然存在电势差和电场，但没有自由电子的运动。那么，电流就不会在电路中流动。因为绝缘体的原子结构不允许自由电子移动。

　　图 2 (b)：两个电极之间的非导电材料图 2 (b)：两个电极之间的非导电材料
　　电阻率

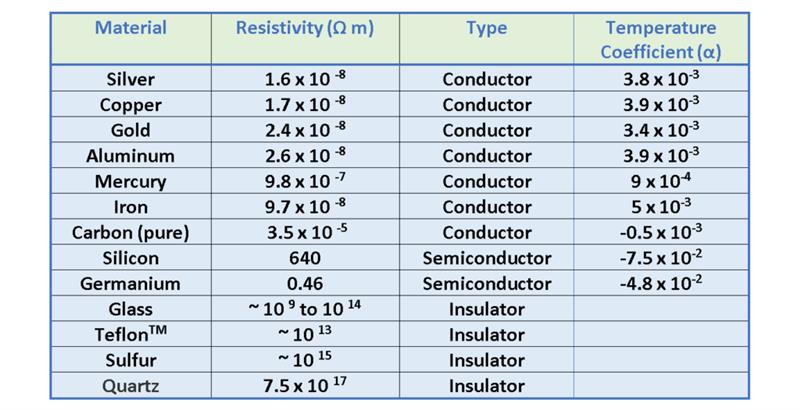
　　我们在上一篇文章中已经从微观角度考虑了漂移速度的概念。在导电体内，电子因与内部电场 ( E ) 相关的电力加速而获得速度，从而使其获得与电场相反方向的速度。本质上，携带电流的自由电子不会沿直线路径穿过导体。相反，它们会与金属原子反复碰撞。与原子的碰撞使电子的速度随机化，使其在与场相反的方向上减小。然后该过程会重复进行。这些碰撞对电子的影响类似于机械系统中的内摩擦力。它会导致自由电子移动到目的地的速度降低。这种现象是材料电阻率的起源。电阻率本质上是材料的基本属性，用于量化材料抵抗电流流动的强度。电阻率是材料的固有属性，不取决于其尺寸或形状。每种材料都具有取决于其电子结构和温度的特征电阻率。电阻率用“ρ”表示，以欧姆米 (Ω.m) 为单位进行测量。良好的电导体具有非常低的电阻率，良好的绝缘体具有非常高的电阻率。表2列出了20℃时各种材料的电阻率。不同的材料具有截然不同的电导率和电阻率值：铜等导体具有高导电性（低电阻率）木材等绝缘体的电导率非常低（电阻率高）因此，电导率和电阻率之间的数学关系如公式 2所示：

　　方程 2：电阻率和电导率的倒数
　　这意味着它们是互逆的。虽然这种数学关系表明了完美的互惠关系，但在现实世界的测量中，这种互惠并不总是直接或的。例如，金属通常更紧密地遵循相互关系，而半导体和复杂材料可能会表现出显着的偏差。本质上，不同材料的电导率和电阻率有一些影响因素；例如，原子或分子结构以及温度变化。在科学和工程应用中，研究人员经常使用实际测量，而不是仅仅依赖理论 1/ρ 关系。这意味着在特定条件下仔细测量电导率和电阻率，以了解材料的真实电气行为。
　　电阻率的温度依赖性

　　对于大多数金属，电阻率随着温度的升高而增加。这种相关性可以理解如下：随着材料温度的升高，其组成原子的振动幅度更大。结果，电子发现更难以通过这些原子，就像人们运动时比静止时更难以穿过拥挤的房间一样。因此，随着温度升高，电子散射增加，导致电阻率增加。在有限的温度范围内，根据公式3，大多数金属的电阻率随着温度的升高而增加：

　　公式 3：以温度表示的电阻率

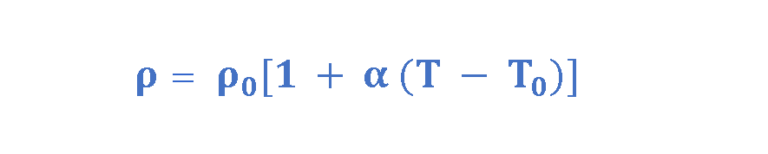
　　其中“ρ”是某个温度 T（摄氏度）下的电阻率，“ρ 0 ”是某个参考温度“T 0 ”（通常取 20°C）下的电阻率，“α”是一个称为电阻率温度系数。表 2还提供了各种材料的温度系数。

　　表 2：各种材料的电阻率和温度系数（20°C 时）
　　表2表明：对于大多数金属，电阻率随着温度的升高而增加，而对于半导体，则电阻率降低。
　　电阻

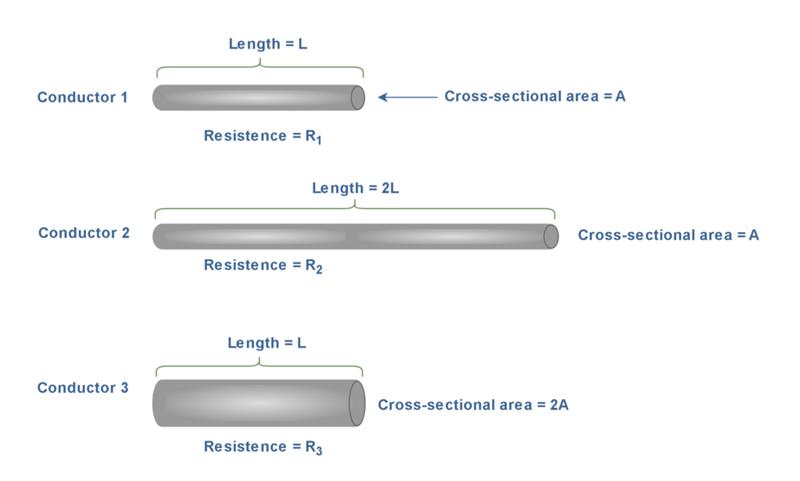
　　电阻也是衡量物体在施加电压时阻碍电流流动的程度的指标。电阻取决于电阻率 ρ（材料的自然特性）和物体的尺寸。我们可以再次参考图 1来考虑圆柱形导体的电阻。首先，导体的电阻随着长度的增加而增加，这是有道理的，因为穿过导体的电子必须在较长的导体中经历更多的碰撞。其次，较小的横截面积也会增加导体的电阻，就像较小的管道会减慢流体流过它的速度一样。那么，电阻与导体的长度“L”成正比，与其横截面积“A”成反比。公式 4根据以下关系定义了导体的电阻 R：

　　公式 4：以导体的电阻率、长度和横截面积表示的电阻

　　其中比例常数 ρ 称为材料的电阻率，单位为欧姆米 (Ω.m)。 L和A的尺寸分别为米(m)和平方米(m 2 )。电阻值以欧姆 (Ω)为单位测量。电阻也是大多数实用电子设备的一个特性，无论是否需要。对于许多材料，包括大多数金属，实验表明电阻在很宽的施加电压或电流范围内保持恒定。图 3显示了三个相同材料（相同电阻率 ρ）但尺寸不同的导体棒。

　　图 3：比较 3 个材料相似但尺寸不同的导体之间的电阻
　　通过使用公式 4，我们可以计算并比较它们的电阻 R 1、R 2和 R 3。导体 2 具有与导体 1 相同的横截面积 (= A)，但长度加倍 (= 2L)。因此，其电阻（R 2）为导体1电阻的2倍，即R 2 = 2 ρl/A = 2R 1。导体 3 与导体 1 具有相同的长度 (= L)，但横截面积加倍 (= 2A)。因此，其电阻（R 3）为导体1电阻的一半，即R 3 =ρl/2A=R 1 /2。图 3说明了即使材料属性保持不变，导体的电阻也如何根据其物理尺寸而变化。由于根据公式 3 ，具有均匀横截面的导体的电阻 (R) 与电阻率成正比，因此电阻的温度变化可写为公式 5：

　　公式 5：电阻的温度变化

　　其中“R”是某个温度T（摄氏度）下的电阻，“R 0 ”是某个参考温度“T 0 ”（通常为20°C）下的电阻，“α”是电阻率温度系数。
　　电路理论的欧姆定律

　　如图 1所示，当电压（电位差）ΔV 施加在金属导体的两端时，导体中的电流“I”与施加的电压成正比（I ~ ΔV）。然后，我们可以写出方程6，其中比例常数是导体的电阻：

　　公式 6：电压、电流和电阻方面的欧姆定律

　　其中“I”是电流（单位为安培），“ΔV”是电压（单位为伏特），“R”是以 SI 单位伏特/安培测量的电阻，称为欧姆(Ω)。根据定义，如果导体上 1 V 的电位差产生 1 A 的电流，则导体的电阻为 1 Ω。这是电路理论中电阻的另一个众所周知的定义。方程 6的这一表述被称为电路理论欧姆定律，以Georg Simon Ohm（1789-1854）命名，他是位对电阻进行系统研究的德国物理学家。这实际上是公式 1的一个特例。在讨论电路时，我们继续使用这种传统形式的欧姆定律。该定律在电气工程中有很多实际应用。电流、电压和电阻的概念可以与河流中的水流进行比较。当水在宽度和深度恒定的河流中向下流动时，流速（水流）取决于河流源头的陡度以及岩石、河岸和其他障碍物的影响。电压差类似于陡度和对障碍物的阻力。基于这个类比，增加施加到电路的电压应该增加电路中的电流似乎是合理的。此外，增加电路中的电阻会降低电流。欧姆定律是一种仅对某些材料有效的实际关系。遵守欧姆定律并因此在很宽的电压范围内具有恒定电阻的材料被称为欧姆材料。电阻随电压或电流变化的材料是非欧姆材料。换句话说，欧姆材料在大范围的施加电压下具有线性电流-电压关系和恒定斜率，如图4 ( a )所示。但非欧姆材料具有非线性电流-电压关系（没有恒定的斜率），如图4 ( b ) 所示。

　　图 4：(a) 欧姆材料和 (b) 非欧姆材料的电流-电压曲线
　　电子系统中大多数简单的电阻器具有恒定斜率的线性电流-电压关系，而现代半导体电子器件，例如二极管和晶体管，具有非线性电流-电压关系，并且不遵守欧姆定律。