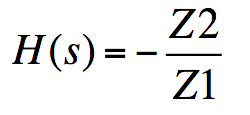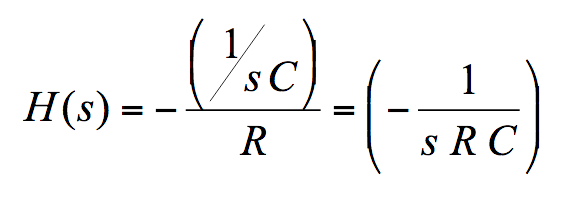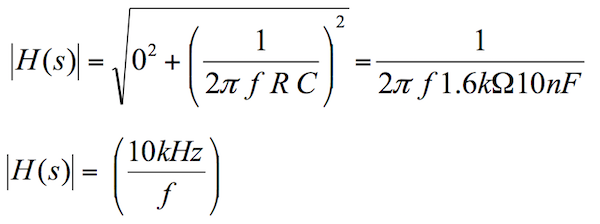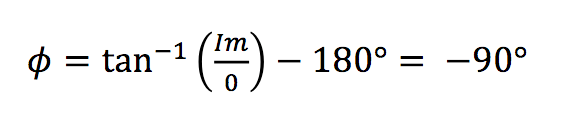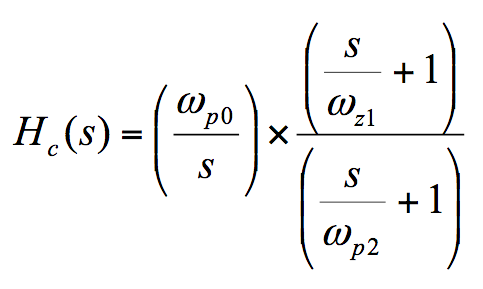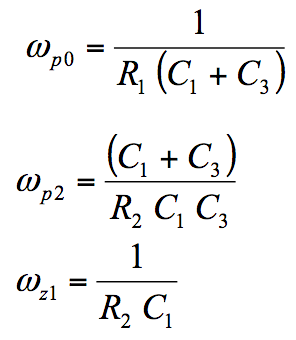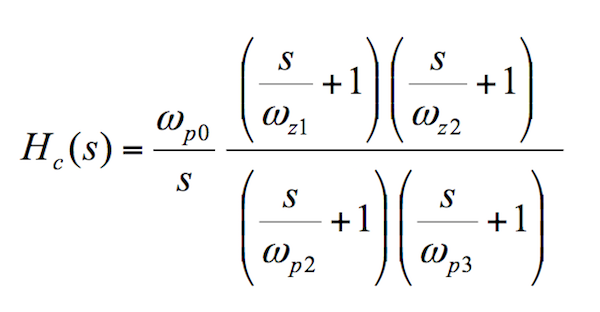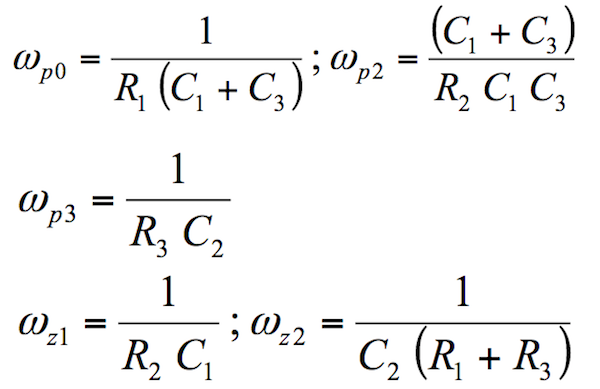我们介绍了了解电源补偿器设计基础知识所需的所有基础材料。在本文中,我们将讨论电源中常用的补偿器。我们将解释它们的电路、传递函数及其极点和零点。
在大多数情况下,PSU 的模拟补偿器采用反相
运算放大器的形式,通常位于控制器 IC 内部,加上一些外部
电容器和
电阻器。当然,电容器和电阻器根据运算
放大器电路的传递函数确定极点和零点的位置。基于之前文章中介绍的材料,我们现在处于讨论该主题的理想位置。
关于 PSU 补偿器需要记住的一件事是它们没有什么可怕的。我们只是处理一个具有一些阻抗的反相运算放大器,就像我们在大学的前几堂讲座中所学习的那样。
考虑图 1 中的通用反相运算放大器
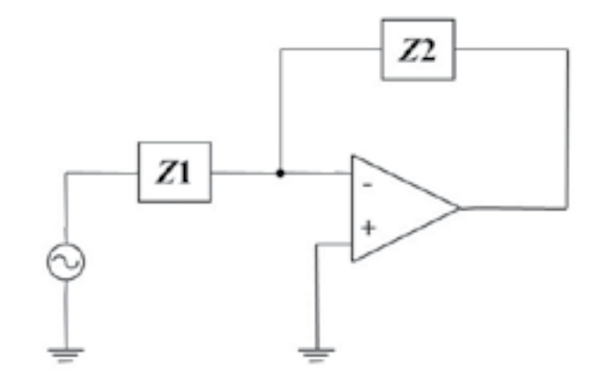
图 1 – 通用反相运算放大器
我们从大学讲座中得知,该电路的传递函数为:
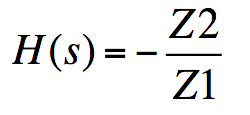
eq1_Bricha 讲义
其中Z1和Z2通常是电容器和电阻器的组合。通过这个简单的电路,我们可以构建几乎所有模拟电源中使用的补偿器。
I型补偿器
如果我现在用电容器 (C = 10nF) 替换 Z2,用电阻器 (R = 1.6kΩ) 替换 Z1,我将为自己创建一个简单的 I 型补偿器。此外,通过选择电容器和电阻器的值,我可以控制该补偿器具有的任何极点和零点的位置。请注意,为了简化教学,我们不考虑通常连接到同相输入的直流参考源和通常连接在反相输入和地之间的偏置电阻。这两个元素仅影响直流分析,不会影响我们补偿器的交流传递函数;换句话说,它们对我们的极点和零点的位置没有影响。
因此我的传递函数变为:
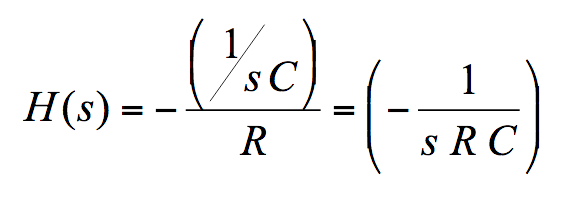
eq2_Bricha 讲义
我在某个频率 f 的增益将是:
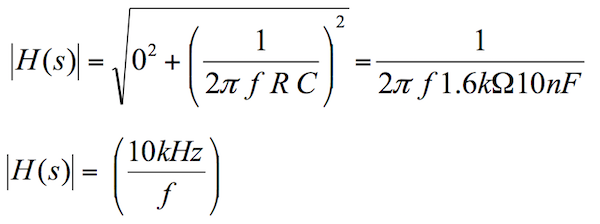
eq3_Bricha 讲义
考虑到运算放大器的反相作用,相位 f 将为:
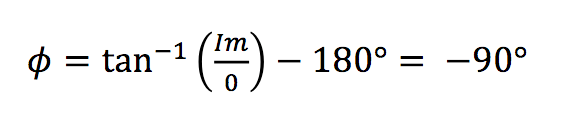
eq4_Bricha 讲义
看看上面的方程,有一些非常重要的观察结果需要指出:
我们在原点有一个极点,因为只有当 s = 0 时,传递函数的分母才变为零。
从增益方程我们可以看出,低频时的增益接近无穷大。一般来说,这正是我们想要的电源,因为低频下的高增益转化为接近零的稳态误差。
再次从增益方程我们可以看到,当 f = 1/ (2 p RC) 时,即当 f = 10kHz 时,增益变为 1。这意味着在 dB 世界中,增益图与零 dB 轴交叉。许多教科书或应用手册称之为“原点极点位置”。它们实际上的意思是“原点极点增益穿过 0 dB 点的频率”。
这是我们从现在开始将使用的术语。因此,从现在开始,每次我们说“我们将极点置于某个频率处的原点”时,我们的意思是选择电阻器和电容器的值,使得原点处极点的增益图在某个频率处与 0 dB 交叉。一定的频率。
从相位方程我们可以看到相位滞后为-90°。这当然是我们系统中单极的特点。
I 型补偿器在高性能电源中相对较少,我们将其包含在此处用于教学目的并解释原点磁极位置的概念。 II 型和 III 型补偿器更为常见,占绝大多数。让我们来看看它们。
II型补偿器
这是的补偿器之一,因为它几乎总是用于电流模式电源。我们将在后面的文章中讨论电流模式控制。
图 2 给出了包括简单降压功率级的电路。
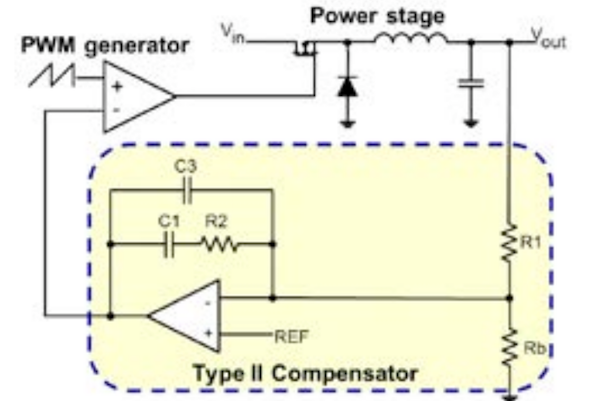
图 2 – II 型补偿器电路。请注意,PWM 发生器和运算放大器通常位于我们的 IC 内部
该补偿器的传递函数为:
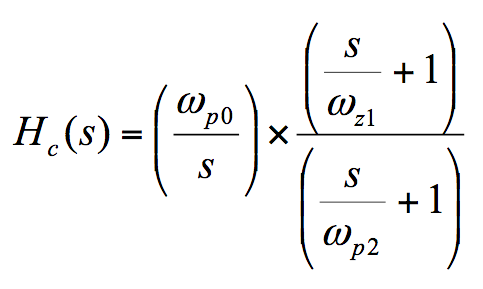
eq5_Bricha 讲义
回顾我们之前的讲义,我们可以立即识别出原点处有 1 个极点 (wp0)、第二个极点 (wp2) 和零极点 (wz1)。请注意,方程以 rad/s 为单位,并且组件值始终决定这些极点和零点的位置:
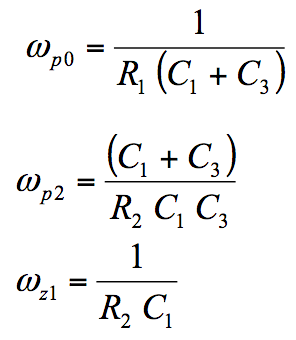
eq6_Bricha 讲义
很容易看出,通过适当选择元件值,我们可以放置极点和??零点来塑造波特图,从而满足前面文章中讨论的稳定性标准。
您可以从传递函数中看到我们有一个零。这当然意味着我们可以强制相位提升 90°。但有时 90° 相位提升还不够;一个例子是我们几乎所有的电压模式电源。因此,我们需要另一个允许更多相位提升的补偿器;这是我们的 III 型。
III型补偿器
我们的 III 型补偿器的电路如图 3 所示
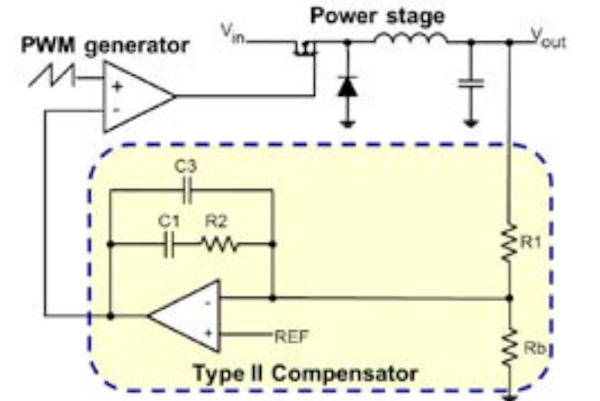
只需添加一个额外的电阻器和电容器(R3 和 C2),我们就可以将 II 型补偿器转换为 III 型补偿器,并获得我们需要的额外相位升压。传递函数如下:
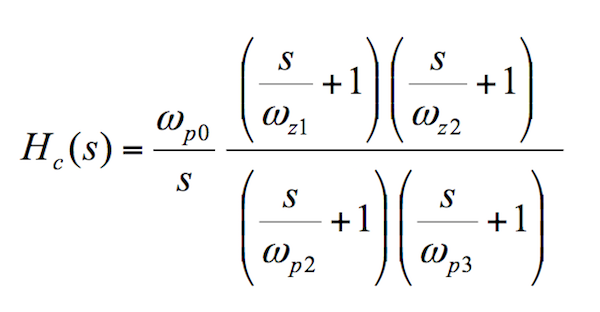
eq7_Bricha 讲义
现在我们可以看到,我们在原点再次拥有了理想的极点,以消除稳态偏移,但这次与我们的 II 型补偿器相比,我们有一个额外的极点 (wp3),更重要的是,还有一个额外的零 (wz2)。当然,2 个零的存在表明我们可以实现 180° 的相位提升,而 II 型的相位提升为 90°。
确定极点和零点位置的方程是:
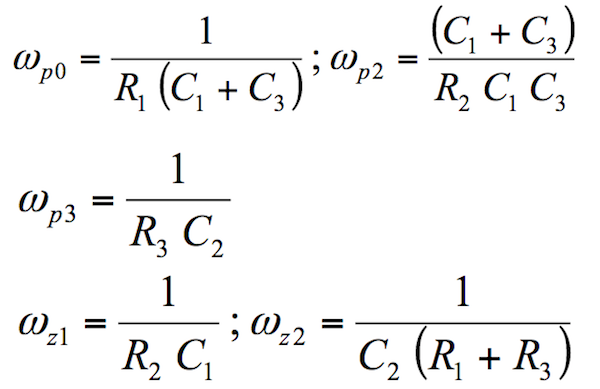
eq8_Bricha 讲义
传递函数与现实的匹配程度如何
好消息是,仅通过这两个传递函数,我们就可以稳定世界上大多数模拟电源。我们将在以后的文章中学习如何放置极点和??零点以及逐步的现实生活设计。现在,让我们尝试一下电阻器和电容器的值来放置极点和??零点,然后测量真实的补偿器,看看它是否与我们的理论相符。
我们将使用 Biricha Digital 的自动化电源设计软件首先设计 III 型补偿器,然后使用 Bode 100 网络
分析仪进行构建和测量。从图 4 中可以看到,Bricha WDS 已经放置了补偿器的极点和零点并计算了元件值。图 4 的右栏中给出了接近的组件优选值。
将元件值插入上述 III 型补偿器的方程中,应给出与 WDS 计算的完全相同的极点和零点,如图所示。请注意,前面给出的方程的单位是 rad/s,但在 WDS 中它们的单位是 Hz。目前我们对零极点放置策略不感兴趣;我们将在后面的文章中讨论详细设计。现在,我们只是确保我们的方程是正确的,并且模拟的频率响应与现实生活中的频率响应非常吻合。
仿真波特图与实际补偿器的实际测量值与图 4 的元件值之间的比较如图 5 所示。您可以看到我们几乎完美匹配,因此我们的方程是正确的并且元件值准确放置补偿器的极点和零点恰好位于我们期望的位置。
我们现在需要做的就是设计一种放置极点和??零点的策略,以便满足我们的规格和稳定性标准。我们将在接下来的几篇文章中详细介绍这一点。