干扰信号 每次测量都包括感兴趣的信号和不需要的信号的集合,例如噪声、干扰和失真。噪声和干扰通常与被测量的信号无关。失真是干扰信号或与感兴趣信号相关的信号,例如谐波。
噪声是一种由其统计特征描述的随机信号。干扰包括通过串扰等过程耦合到测量系统中的信号。干扰信号本质上通常是周期性的。
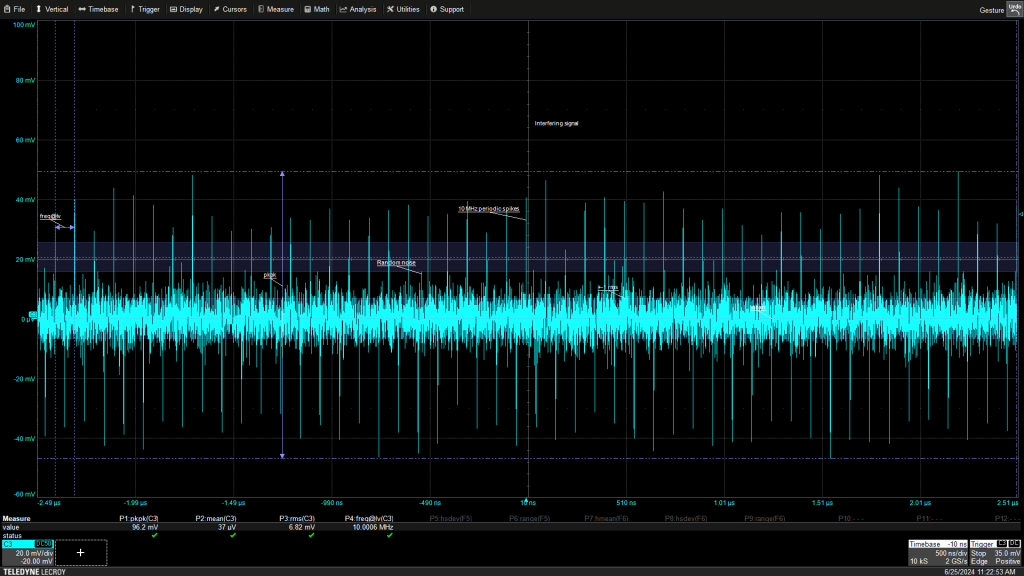
图 1显示了包含随机和周期性分量的干扰信号的示例以及用于表征信号的一些工具。示波器在周期元素上触发。
干扰信号包含随机和周期性分量。周期分量由 10 MHz“尖峰”组成。电平频率 (freq@lvl) 测量参数(显示网格下方的 P4)读取信号幅度大约 70% 处的尖峰频率,以避免噪声峰值。此外,还测量平均值、峰峰值和均方根电平。数字化仪器,包括示波器和数字化仪,有多种工具可以测量此类噪声信号的特征。他们还提供一系列分析工具来减少这些不需要的信号元素的影响。
仪器噪音 所有数字化仪器也会给测量带来噪音。通常,选择噪声水平低得多且不影响测量的仪器。根据测量应用,可以选择具有 8 位或 12 位分辨率的示波器以及具有 8 位至 16 位或更高幅度分辨率的数字化仪,以将仪器噪声保持在合理范围内。
差分连接 当减少噪声和干扰信号时,数字化仪器的输入是起点。一个好的起点是使用差分连接来减少共模信号。许多数字化仪和一些示波器具有差分输入,而示波器通常提供差分探头来将被测设备 (DUT) 连接到仪器。
差分信号使用由互补信号驱动的两条电线来传输信号。当计算两条线路之间的电压差时,两条导线共有的噪声和干扰(共模信号)将被消除。共模抑制比 (CMRR) 衡量共模噪声被抑制的程度。另请注意,差分信号也不需要接地回路。在某些情况下,这还有助于限度地减少干扰信号的拾取。差分信号传输的一个示例是控制器局域网或 CANbus,如图 2所示。
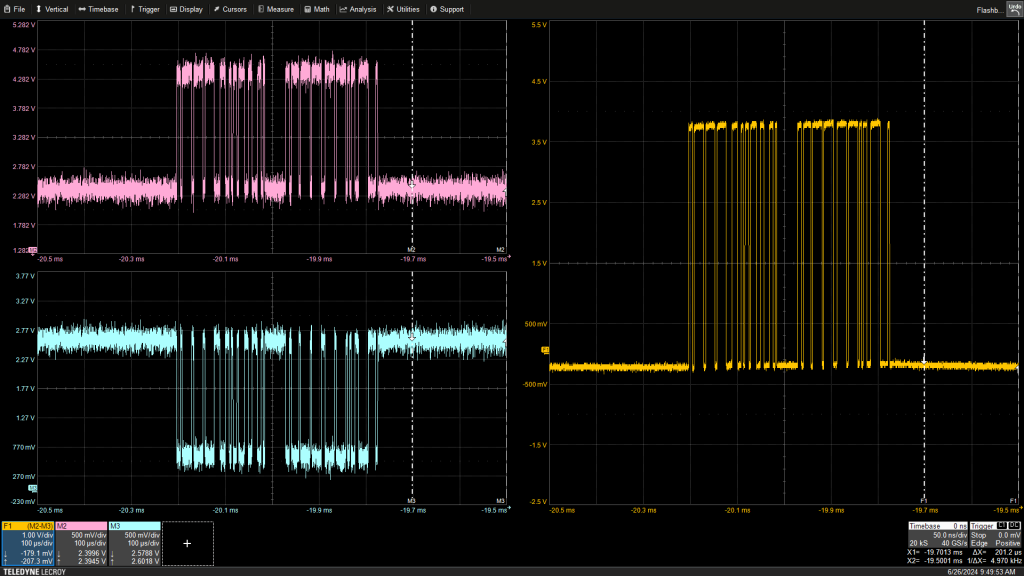
图 2 CANbus 的两个差分组件(左侧)以及由此产生的差异,显示共模噪声有所降低。资料阿瑟·皮尼
两个 CANbus 信号分量是互补的,当一个分量从另一个分量中减去时,共模信号(例如噪声和干扰)就会抵消。请注意,两个组件之间的差异是单个信号电压摆幅的两倍,从而使 SNR 提高了 6 dB。
差分探头或差分
放大器中的差分操作可降低两条线路的共同噪声,从而允许更长的
电缆运行。除了 CANbus 之外,差分信号在 RS-422、RS-485、双绞线以太网以及其他串行数据通信链路中也很常见。
通过使用双绞线或同轴传输线可以进一步减少差分信号中的共模噪声和干扰,这些传输线可以提供额外的屏蔽以防止干扰源。
数字化仪器工具以减少噪音和干扰。
示波器和数字化仪可以对干扰信号执行各种测量和分析。平均会降低随机分量的幅度,而背景扣除可以从波形中去除周期性分量。图 3显示了使用这些工具对图 1 中所示的干扰信号进行的分析。
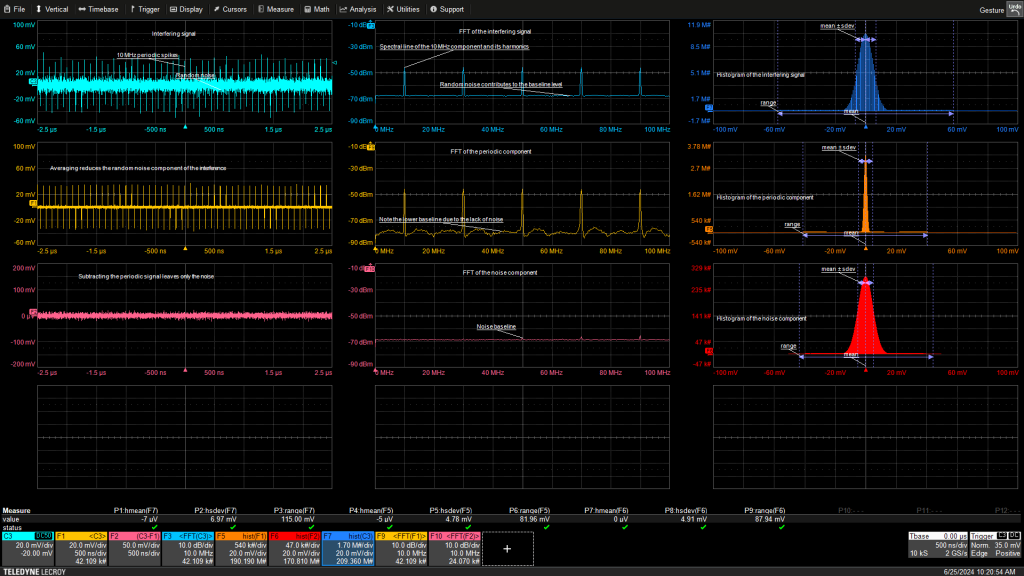
图 3使用平均和背景扣除来分离干扰信号的随机和周期性元素。资料阿瑟·皮尼
干扰信号出现在左上方网格中。右边是干扰信号的快速傅立叶变换 (FFT)。垂直谱线与周期分量相关。周期性窄脉冲序列的基波分量为 10 MHz,它以接近恒定的幅度在所有奇次谐波频率上重复。随机元素在频谱上平坦且在所有频率上具有相同的能量,显示为 FFT 频谱的基线。右上方的网格包含干扰信号的直方图。随机成分在直方图中占主导地位,呈现出钟形正态分布。
对干扰信号进行平均将减少随机噪声分量。如果噪声分量呈高斯分布或正态分布,则信号幅度将与平均值数量的平方根成比例地减小。平均波形出现在中左网格中;请注意基线上不存在随机成分。平均波形的 FFT 位于中心网格中,从顶部向下数第二个。请注意,谱线的幅度仍然相同,但基线降至约 -80 dBm。由于噪声降低,直方图具有小得多的钟形响应。直方图的范围测量读取从峰值幅度到谷值幅度或峰峰值幅度的幅度。
在采集时从干扰波形中减去平均背景波形将消除大部分周期性波形。这个过程称为背景扣除。它适用于背景信号稳定的情况,并且可以从中触发示波器。生成的波形出现在左侧底部网格中。该信号的 FFT 位于占用的底部中心网格中。请注意,其频谱大部分是平坦基线,幅度约为 -68 dBm,与原始 FFT 中的基线水平相同。 10 MHz 周期信号的谐波频率处存在一些小谱线,这些谱线未被减法运算消除。它们小于原始谐波幅度的百分之十。分离的随机分量的直方图具有高斯形状。由于不存在周期性分量,其范围低于原始直方图。
对真实信号使用背景扣除要求在应用信号之前捕获背景并对其进行平均。然后从采集的信号中减去平均背景。
清理真实信号
让我们研究一下如何减少所采集信号的噪声和干扰。感兴趣的信号是 100 kHz 方波,如图 4左上方网格所示。
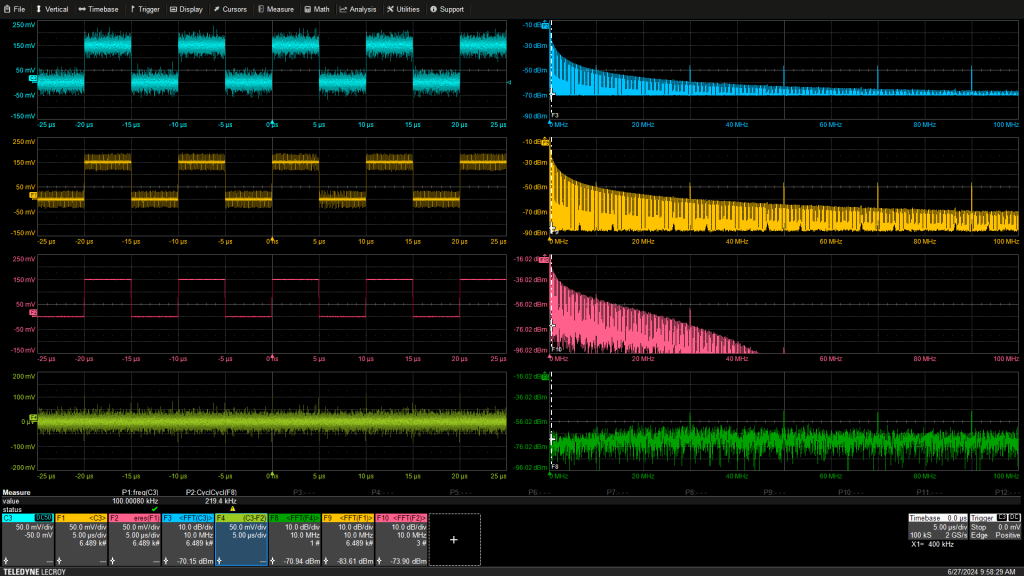
图 4使用平均和滤波减少 100 kHz 方波的噪声和干扰。资料阿瑟·皮尼
我们一直在研究的干扰波形已添加到 100 kHz 方波中。示波器在 100 kHz 方波上触发。 FFT 出现在右上方的网格中。频谱由方波频谱组成,其谱线为 100 kHz,并在其所有奇次谐波处重复,其幅度随频率呈指数下降。 10 MHz 干扰信号提供 10 MHz 的谱线及其所有奇次谐波,这些谱线在 FFT 的整个跨度上具有均匀的幅度。随机分量将 FFT 基线提高到约 -70 dBm。
对波形进行平均(左侧下方的第二个网格)会消除随机分量,但不会消除周期性分量。平均信号(右下第二个)的 FFT 与之前一样显示 100 kHz 和 10 MHz 分量,但由于随机分量的减少,FFT 的基线降至约 -90 dBm。平均不会影响周期分量,因为它与示波器触发同步。
滤波可以降低噪声和干扰水平。该示波器的输入信号路径中包含 20 MHz 和 200 MHz 模拟
滤波器。它还包括六个有限脉冲响应低通数字滤波器,称为增强分辨率 (ERES) 噪声滤波器。左侧下方的第三个网格显示使用 ERES 滤波器过滤的信号。这是一个低通滤波器,-3 dB 截止频率为 16 MHz。信号看起来相当干净。滤波器的效果可以在右侧滤波信号的 FFT 中看到。低通滤波器可抑制 16 MHz 以上的频谱分量。虽然这种方法有效,但您必须小心,低通滤波会抑制所需信号的谐波,并可能影响过渡时间等测量。
ERES 噪声滤波器可用的六个带宽随仪器采样率的变化而变化,限制了它们的实用性。该示波器还具有可选的数字滤波器包,可提供更广泛的滤波器类型和截止特性,从而优化噪声和干扰降低。
通过背景从采集的波形中减去滤波后的波形,我们可以看到滤波器去除了哪些内容(左下网格)。 FFT(右下网格)显示缺失的 10 MHz 和 100 kHz 谐波。
通过数字化仪器限度地减少噪音
在数字化仪器测量中限度地减少噪声影响的关键技术包括差分采集、平均以减少宽带噪声、背景扣除以及滤波以减少噪声和周期性信号干扰。



