FFT(快速傅立叶变换)早出现在 20 世纪 70 年代
微处理器进入商业设计时。如今,几乎每台
示波器(从高价实验室型号到价业余型号)都提供 FFT 分析。FFT 是一种功能强大的工具,但要有效使用它需要一些研究。我将向您展示如何设置和有效使用 FFT。我们将跳过 FFT 的技术描述,因为它已经在仪器中实现。相反,我将重点介绍使用这个伟大工具的实际方面。
FFT 是一种减少离散傅立叶变换 (DFT) 计算时间的算法,DFT 是一种分析工具,可让您在频域 (幅度和相位与频率) 中查看获取的时域 (幅度与时间) 数据。本质上,FFT 为数字示波器添加了频谱分析。
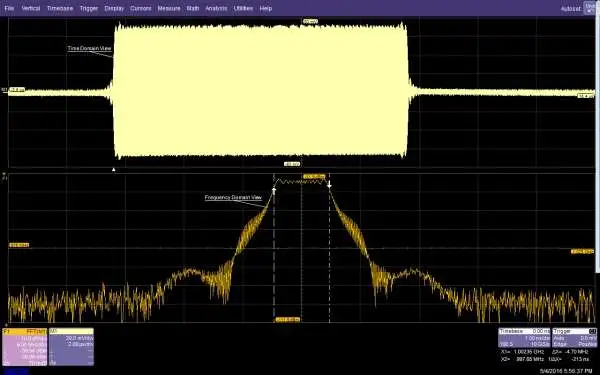
如果您查看图 1中的上部迹线,您将看到一个使用梯形脉冲作为调制函数的幅度调制载波。如果您查看图 1 中的时域视图,并且我要求您告诉我信号的带宽,您会很难回答。但是,对该信号进行 FFT,您会得到另一个视角。信号具有线性扫描频率,带宽(由光标标记)为 4.7 MHz。这就是 FFT 如何增加示波器的功能,它为同一数据提供了另一个视角。
FFT 频率跨度和分辨率带宽
在早的电路课程中,您了解到周期信号的频率(频域)是周期(时域)的倒数。相同的关系在整个 FFT 设置中出现。
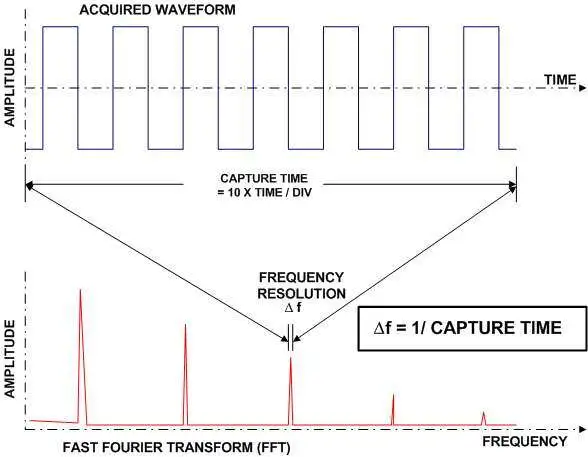
设置 FFT 的起点是选择 RBW(分辨率带宽),因为它与单一设置相关。RBW(Δf)是显示 FFT 频率轴的增量步骤。在时域中,采样周期决定样本之间的时间。在频域中,RBW 是频谱视图中相邻“单元”之间的频率差。RBW 是时域记录长度的倒数,也称为捕获时间,如图2所示。您可以使用示波器的水平刻度或时间/分度设置来控制它。图 1 中的采集持续时间为 20 ?s。因此,频谱视图的 RBW 是该数字的倒数,即 50 kHz。
FT 设置的下一步是确定频域视图的跨度——FFT 中频率和频率之间的差值。请注意,FFT 通常从 0 Hz 开始,一直到跨度。这与 RF
频谱分析仪有很大不同,我将在稍后解释。
FFT 的跨度是示波器有效采样率的一半(图 3)。时域中的时间增量(采样周期)决定了频域中的元素。同样,频域中的增量是时间记录中持续时间的函数。这就是时域和频域之间的相互关系。

图 3. 频谱跨度是示波器有效采样率的一半。
为了在频域中实现更精细的分辨率,您必须通过增加时间/分频设置来增加捕获的数据量。这与增加示波器时域视图中的时间分辨率的做法相反。
从实际角度来看,时域记录长度由示波器的时间/分频控制设置。一旦您选择了实现所需的分辨率带宽,控制采样率以实现所??需跨度的方法是更改??示波器的采集
内存长度。现在这似乎很复杂,但事实确实如此。
近期,大多数高端示波器制造商已将 FFT 用户界面改为更接近标准 RF 频谱
分析仪,以分辨率带宽作为参数来设置中心频率和跨度。虽然这种类型的界面使 FFT 更易于使用,但它确实隐藏了 FFT 的底层功能,导致必须接受示波器设置的时间/分频、采样率和内存长度的组合。使用本节讨论的规则,您可以手动设置 FFT 并在设置中实现更大的自由度。
垂直缩放
根据您的示波器,FFT 可能提供多种垂直刻度选择,也可能是单一固定垂直格式。常见的垂直格式是功率谱,它以功率为单位显示垂直幅度。常见的是,它以相对于毫瓦 (dBm) 的分贝表示,并以对数垂直刻度显示。这种选择也是 RF 频谱分析仪的保留。实验室级示波器提供更多可能性,包括 PSD(功率谱密度)、线性幅度、幅度平方、相位或实部/虚部。
PSD 是归一化为 FFT 分辨率带宽的功率谱值。其测量单位为 dBm/Hz,表示单位带宽的功率。PSD 可用于测量噪声等宽带现象。幅度格式显示示波器测量的线性单位的频谱幅度,例如伏特或安培。
幅度平方显示,顾名思义,将频谱振幅显示为幅度的平方。单位可以是伏特?、安培?等,当归一化为仪器的输入阻抗(通常为 50 Ω)时,可为功率测量提供线性缩放。归一化是使用示波器的重新缩放功能完成的,该功能允许乘以常数。对于 50 Ω,幅度平方频谱乘以 0.02(即 1/50),并将单位更改为瓦特(V?/50),以适应 50 Ω 输入阻抗。
FFT 频谱是一个复函数(从数学意义上讲),幅度显示只是图像的一半。FFT 输出由实部和虚部组成。有些示波器可以同时显示这两个部分。作为实部和虚部的替代,许多示波器显示 FFT 相位和幅度。这两种成对的输出格式(实部/虚部和幅度/相位)代表了 FFT 的完整图像。实部/虚部是计算逆 FFT 所必需的。它们在振动测量等机械应用中也更常用。幅度/相位格式在电气测量中更常见。图 4 显示了方波功率谱幅度/相位和实部/虚部的示例。
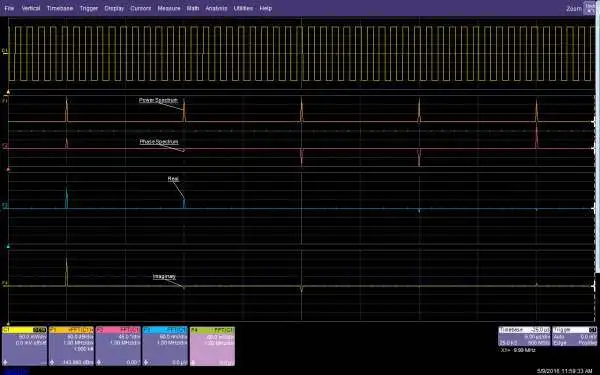
图 4. 方波 FFT 的功率谱幅度、相位、实部和虚部。
相位谱的垂直单位为度,实数和虚数格式的垂直单位与源通道相同,在本例中为 mV。对于周期性波形(例如此方波),相位、实数和虚数格式仅在基频和谐波频率下才具有有效值。
加权函数
示波器中实现的 FFT 具有有限的记录长度。由于所获取波形的起点和终点存在连续性问题,这可能会导致频谱显示出现问题。图 5 显示了起点和终点如何影响频谱形状。
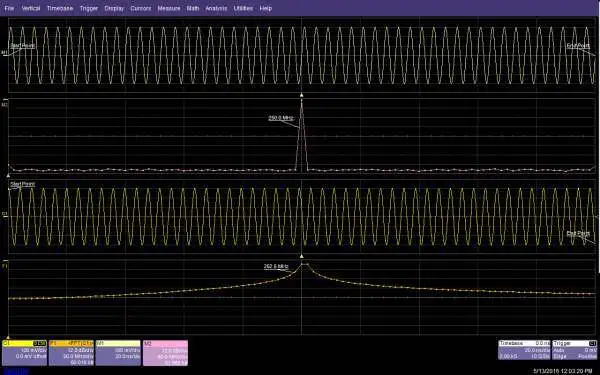
图 5. 起点和终点的边界条件会影响信号经过 FFT 后的频谱形状。
上面两格采集到的信号频率是采样率的约数,采集到的波形有整数个周期,起始点和终止点的幅度相同,得到的频谱很窄;下面两格采集到的信号频率不是采样率的约数,起始点和终止点处于不同的电平。
这会导致时间记录不连续。由于频谱扩展(称为泄漏),因此产生的频谱更宽,峰值水平更低,因为来自所获取信号的能量会分散到相邻的频率单元上。较低的频率相关峰值响应称为“栅栏”效应或扇贝损失。加权(窗口)可以帮助限度地减少这些影响。
加权将采集的波形乘以窗口函数,将其调制为零端点。窗口函数的形状决定了光谱响应,包括谱线的形状和任何边带的幅度。常用加权函数的特性如表 1所示。
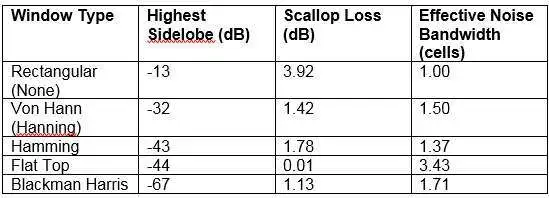
表1. 常见FFT加权(窗口)函数的特点。
表格总结了每个窗口化旁瓣和扇形损失的能力。图 6 显示了窗口函数对同一输入信号的谱线产生的影响。
图 6. 该屏幕图像比较了加权函数对同一输入信号的光谱响应的影响。
谱线变宽可减少扇贝损失,这是有道理的,因为相邻单元中的信号将以更高的振幅重叠,从而获得更广泛的响应,从而限度地减少扇贝损失。
窗口函数的选择取决于您的需求。如果您测量的瞬态小于采集窗口,则不要使用窗口函数,因为频谱峰值的幅度将根据瞬态在采集窗口中的位置而变化。在这种情况下,矩形窗口(无加权)是选择。较窄的窗口响应提供更好的频率分辨率,而较宽的响应(Blackman Harris 或 Flat Top 窗口)可产生更准确的幅度测量。如果您需要两者,那么一个很好的折衷方案是 Von Hann 或 Hamming 窗口。
频域平均 平均
用于提高采集信号的信噪比,通常需要多次采集。平均可以应用于时域或频域。与触发事件不同步的信号(如噪声)会随着平均次数的增加而衰减。
频域平均可改善信噪比,从而提供更大的测量动态范围。噪声信号的 FFT 包含噪声,但 FFT 会在多次采集后取平均,从而使较低水平的谐波可见。
频域中的平均化是通过对多次采集中每个频率单元的内容求和,然后除以采集次数来实现的。与采集不同步的信号平均为零,而同步信号相干地相加。在图 7 中,噪声信号的 FFT 包含频谱扩展的噪声分量。噪声隐藏了低级谐波。平均化可提高信噪比,降低噪声并使谐波可见。以类似的方式,任何与采集不同步的信号的幅度都将减小。
设置示例
考虑需要在 4 GHz 带宽示波器上设置一个 FFT,其跨度为 10 MHz,中心频率为 2.48 GHz,分辨率带宽为 10 kHz,以分析连续的周期性信号。根据前面的讨论,设置分辨率带宽可以通过示波器的时间/分度设置的单一设置来完成。分辨率带宽要求采集或捕获时间为 100 ?s,或时间/分度设置为 10 ?s/分度。应设置示波器的垂直灵敏度(伏特/分度),以使信号占据输入范围的至少 90%,从而化动态范围。
FFT 的跨度由采样率控制。跨度必须包括 2.48 GHz 信号频率,这意味着它必须大于该频率的两倍。5 GHz 或更高的频率可以工作。示波器的采样率为 20 GS/s。我们可以通过调整采集内存长度来设置采样率,以使用示波器的时基设置实现采样率。在本例中使用的示波器中,将内存长度设置为 1 MS 可实现 100 ?s 的采集时间,采样率为 10 GS/s。
数学函数 F1 的 FFT 选项卡具有主要的 FFT 设置,并设置为显示功率谱。由于信号被指示为连续的,因此选择 Von Hann 窗口作为加权函数类型,为频率分辨率和幅度平坦度提供良好的折衷。
FFT 选项卡显示分辨率带宽 (Δf) 为 10 kHz,跨度为 5 GHz。缩放选项卡允许您将中心频率设置为 2.48GHz,水平刻度为 1 MHz/p.





