电子电路噪声的入门课程通常首先阐述电阻器开路噪声电压的以下公式:

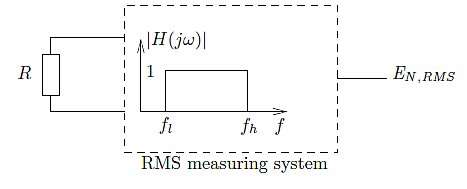
您可能会说这需要满足很多条件;没错,但让我们把事情变得更现实一些。首先,我们要测量的电压很小,所以我们肯定要引入一些放大,比如电压增益为A 而不是 1。然后我们的仪表会显示:
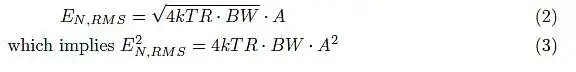
此外,砖墙特性是不可能实现的,因为可以证明这种过滤器是非因果的。所以让我们用可实现的滤波器特性替换它,如图2所示。

如果我们仅考虑无穷小的带宽d f ,这与应用带宽为d f且放大率为|H(jω)|的砖墙滤波器相同 ,则公式3转换为:
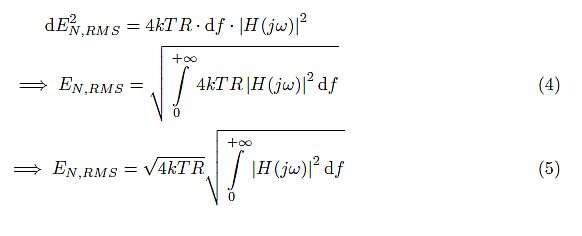
数量

称为噪声等效带宽(NEB ) 1。√4kTR称为 噪声电压密度,我们用时尚的ε来表示它,以避免 与电压E 本身混淆。所以我们也可以写成:
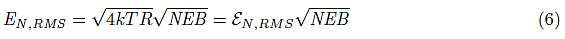
现在,让我们仔细看看公式 6。如果我们使用具有无限带宽的滤波器特性,会发生什么?您可能认为电阻两端的电压是无限的。当然,这在现实中不可能是真的。这里有什么问题?一种解释认为它源于量子现象。公式ε N,RMS = √4 kTR 不是完整的 公式, 它 只是一个近似值,实际上确切的公式是:
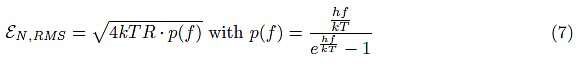
在公式 7 中,h = 6.6261 · 10 -34 [Js] 是普朗克常数。当f趋向 +∞ 时,因子p ( f ) 趋向于零,这将使ε N,RMS 的值保持 有限。让我们针对具有无限带宽的系统检查这一点:

幸运的是,上一行中的积分称为 Bose 积分,有一个已知的简洁解决方案

即使这个解释是正确的,更注重实践的人可能会对量子现象的解释持怀疑态度。谁能责怪他们呢?已故的伟大人物理查德·费曼甚至说过:“如果你认为你理解量子力学,那么你就不懂量子力学。”因此,即使公式 7 解释了为什么你永远不会在电阻端子上得到无限大的电压,在实际电子电路中,还有两个因素将决定电阻的噪声贡献:电阻总是有一些寄生电容和/或带宽限制。寄生电容问题通常在电阻与电容并联时电压的 RMS 值的标准推导中处理:

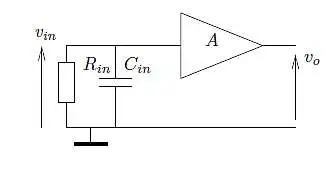
然而,还有一种解释,大多数电子人士更喜欢这种解释,或者至少这种解释让他们相信这种结果:增加并联电阻会增加噪声,但系统的带宽会降低,因此总体结果保持不变。从数学上证明这一点并不难。然而,这是否意味着只有寄生电容很重要?不,因为电阻通常连接到电路中带宽有限的其他部分,所以寄生电容也起着作用。这种系统简单的例子是一个电阻与一个电容器并联,然后是一个一阶系统,如图3所示。
如果我们调用
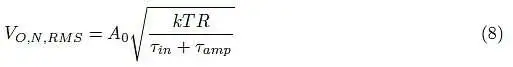
结果简化为:

我们得到结果:
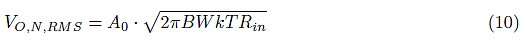
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。