我们看到
强磁场会导致
磁性材料饱和。在饱和材料中,
磁芯中的所有磁畴都与外部磁场对齐。超过该点,就没有其他磁畴可以对齐,从而导致材料磁导率显著下降。虽然有些应用会利用磁芯饱和,但大多数情况下还是应该避免。
当试图防止
电感饱和时,匝数是一个特别重要的设计参数。然而,决定是否需要增加或减少匝数可能有点棘手。在回顾我们将要使用的磁芯响应模型后,我们将了解有关此主题的更多信息。
响应的分段线性模型
磁性材料的 BH 特性具有高度非线性。为了更轻松地分析磁性系统,我们通常使用分段线性函数来建模该曲线。请注意,此分段模型仅考虑饱和度,而不考虑磁滞。
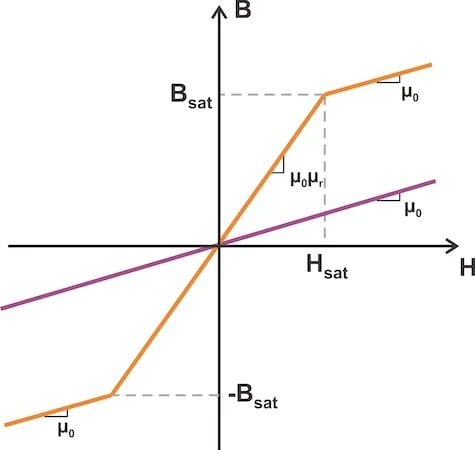
图 1 中的橙色曲线显示了假设铁磁材料 BH 曲线的分段线性近似。为了进行比较,紫色线显示了空芯
电感器的 BH 曲线。
磁性材料 BH 曲线的分段线性模型。还包括非磁性材料的线性 BH 曲线以供比较。
图 1.磁性材料 BH 曲线(橙色)和空芯电感器 BH 曲线(紫色)的分段线性模型。
对于低于饱和点 ( B < B sat ) 的磁通密度,磁性材料的响应近似为恒定的相对磁导率。因此,BH 曲线的这一部分的斜率为μ 0 μ r,其中μ r是相对磁导率,μ 0是自由空间的磁导率。请记住,这只是一个近似值 - 磁性材料的实际响应不是直线。
当B > B sat时,相对磁导率趋近于 1,材料的行为类似于非磁性介质。其 BH 曲线与空芯电感器的 BH 曲线一样,近似为斜率为μ 0的直线。这就是饱和效应。
该图显示,铁磁材料可以具有非常高的磁导率,但前提是它不饱和。当材料饱和时,其磁导率会降低到自由空间的磁导率。然而,实际设计通常将磁通密度设置为低于饱和磁通密度。由于我们可以预期这些设计中的μ r 1,我们可以通过使用水平线近似饱和区域来进一步简化模型(图 2)。
磁性材料 BH 曲线的简化模型,假设磁通在饱和区保持恒定。
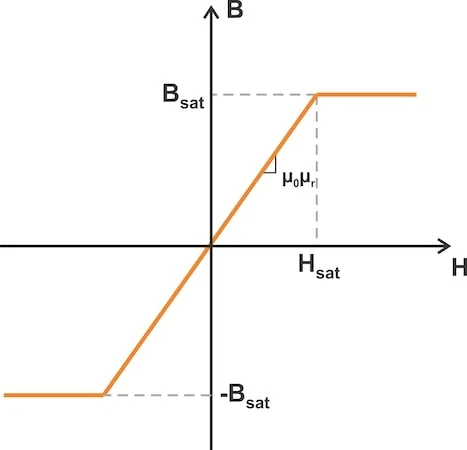
图 2. BH 曲线的简化模型,其中假设通量在饱和区域中保持恒定。
根据法拉第定律,我们知道绕组中感应出的电压与磁通量随时间变化的速率成正比。然而,在饱和状态下,磁通量几乎是恒定的。因此,当电感器磁芯饱和时,电感器上不会感应出电压。相反,电感器的行为几乎像短路一样。
饱和限制磁场力
为了避免饱和,我们需要将磁通密度 ( B ) 限制在B sat以下。我们知道B的计算公式为: B = ?Ac
等式 1.
在哪里:
Φ 是磁通量
c是磁芯的横截面积。
因此,我们可以通过增加磁芯的横截面积或减小 Φ 来限制B。
还必须限制电流与匝数的乘积(nI,即磁场力),以避免磁芯饱和。在给定电流的情况下,增加匝数会导致元件趋向饱和,在给定匝数的情况下,增加电感器的电流也会导致元件趋向饱和。
对于具有n 匝且长度为 l m 的螺线管,磁场强度为H = nI / l m。注意到 Φ = BA c和nI = Hl m,我们可以重新缩放 BH 曲线以获得磁芯的 Φ 与nI曲线。如图 3 所示。
磁芯的磁通量与磁场力曲线。
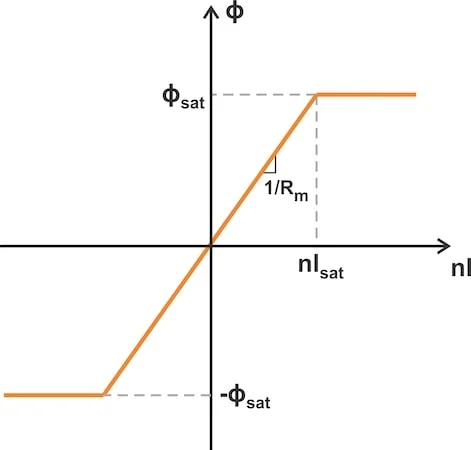
图 3.磁芯的Φ与nI曲线。
为了避免饱和,我们应该:nI ≤ Hsatlm ? nI ≤ Bsatlmμ0μr
等式 2.
我们从复磁导率的讨论中取出磁通密度方程
(B = μ0μrH
) 并将其重写为求解场强度
(H = Bμ0μr)从而得到方程 2 的右半部分。
磁芯饱和度和电感电压
在上面的讨论中,我们假设流过电感器的电流(I)是已知的。在这种情况下,我们可以轻松使用公式 2 来确定磁场力值是否会导致饱和。
然而,我们有时会得到电感两端的电压而不是流经电感的电流,因此需要使用该信息来验证磁芯是否饱和。此外,如果磁芯饱和,我们需要确定可以更改哪些参数以避免饱和。
我们知道电感器的电压和电流的关系为:
V = LdIdt
等式 3.
在哪里:
L是电感
t是时间。
利用这一关系,我们可以根据电感两端的电压计算出电感电流。一旦知道电流,我们就可以使用公式 2 来判断磁芯是否饱和。不过,更直接的方法是直接使用法拉第定律:
V = NdΦdt = NAcdBdt
等式 4.
通过对上述方程进行积分,我们得到了磁通密度与电压的关系:
B(t) = 1NAc∫t0V(t)dt + B(0)
上式明确显示了B和V的时间依赖性。积分还引入了初始B项,形式为B (0),表示初始时间 ( t = 0)时通过电感的磁通量。
公式 5 有另一个重要含义,尽管它似乎违反直觉。它表明,对于施加到电感上的给定电压波形,增加匝数会使电感远离饱和状态。这与在公式 2 中向电感施加给定电流相反。对于流过电感的已知电流,增加匝数会使器件趋向饱和状态。
重新检查公式 4 可以解释这种明显的矛盾。该公式表明,如果我们增加匝数 ( N ),则产生给定电压 ( V ) 所需的磁通量 ( Φ ) 变化相对较小。换句话说,如果施加到电感器的电压波形固定,我们可以增加N以减少通过电感器的磁通量,从而使磁芯远离饱和区。
为了更好地理解这一点,让我们研究一下正弦输入电压的特殊情况。
正弦电压下的磁芯饱和
假设施加到电感器的电压为:
V = Vmsin(ωt)
等式 6.
其中V m是电压的幅度(正弦波的幅度)。
这也会通过电感产生正弦磁通。应用公式 5,我们得到:
B(t) = 1NAc(?Vmωcos(ωt))∣∣∣t0 + B(0)
简化为:
B(t) = VmNAcω(1 ? cos(ωt)) + B(0)
等式 8.
现在,我们来计算B ( t )的峰峰值。注意,输入电压是正弦波,输入电压在 ? t = 0 到 ? t = π 的区间内为正。因此, B ( t ) 与输入电压的积分有关,在 ? t = π 时达到值。求出B (? t = π) 和B (? t = 0)之间的差值,我们就可以计算出B ( t )的峰峰值:
Bpp = 2VmNAcω
等式 9.
为了避免饱和, B ( t )的幅度应小于Bsat 。由于幅度值等于峰峰值的一半(Bp = Bpp /2),因此可得出:
VmNAcω ≤ Bsat
等式 10。
如您所见,对于幅度为V m 的正弦电感电压,我们可以增加N以避免磁芯饱和。公式 10 还表明,降低正弦波的频率 (?) 可以使磁芯趋于饱和。为了理解这一点,请注意通过磁芯的磁通量与输入电压的积分成正比(公式 5)。
降低输入频率意味着输入电压具有更长的正半周期和负半周期。在这些较长的半周期内,磁通有时间增加到更大的正值或负值。因此,存在磁芯可以支持的频率而不会饱和。为了进一步阐明这些概念,让我们来解决几个简单的示例问题。
示例 1
在给定温度下,磁芯材料的饱和磁通密度为 0.2 T。我们利用这种材料构建一个电感器,其磁芯横截面积为 10 -4 m 2,匝数为N = 10。如果电感器两端的电压为正弦波,振幅为V m = 10 V,那么避免磁芯饱和所需的工作频率是多少?
将给定的值代入公式 10,我们得到:
ω ≥ VmNAcBsat = 1010 × 10?4 × 0.2 = 50,000rad/s
从rad/s转换而来,避免磁芯饱和的工作频率为f = 7.96 kHz。
示例 2
电感器设计用于支持幅度为V 1、频率为 ? 1 的正弦电压。此输入的峰值磁通密度为B 1。如果我们将匝数加倍,那么使磁通密度保持在B 1以下的频率是多少?
从公式9可知,磁通密度(B p)的幅度为:
Bp = VmNAcω
等式 12.
由于V m和A c假设为常数,将N加倍可让我们将频率减半,而不会超过原始磁通密度B 1。因此,新电感器可以低至 1 /2。


